2024春八年级数学下学期期末章综合素质评价试卷（华东师大版）

这是一份2024春八年级数学下学期期末章综合素质评价试卷（华东师大版），共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.[2023·内江六中月考]无论a取何值，下列分式总有意义的是( )
A.a－1a2+1B.a+1a2C.1a2－1D.1a+1
2.反比例函数y＝－5x的图象位于( )
A.第一、三象限B.第二、三象限C.第二、四象限D.第一、四象限
3.[2023·南阳三中月考]如图，在▱ABCD中，AB⊥AC，若AB＝8，AC＝12，则BD的长是( )
A.22B.16
C.18D.20
4.[2023·石家庄二十三中月考]在同一直角坐标系中，一次函数y＝kx－k与反比例函数y＝kx(k≠0)的图象可能是( )
5.[2023·大庆]下列说法正确的是( )
A.一个函数是一次函数就一定是正比例函数
B.有一组对角相等的四边形一定是平行四边形
C.两条直角边对应相等的两个直角三角形一定全等
D.一组数据的方差一定大于标准差
6.对于一次函数y＝－2x＋4，下列结论错误的是( )
A.若两点A(x1，y1)，B(x2，y2)在该函数图象上，且x1＜x2，则y1＞y2
B.函数的图象不经过第三象限
C.函数的图象向下平移4个单位长度后得到y＝－2x的图象
D.函数的图象与x轴的交点坐标是(0，4)
7.“双减”政策落实后，同学们更加重视课堂学习，小明和小颖两个人每周做一次数学自我测试，如图是记录了两个人9次测试成绩的折线图，从稳定的角度看两个人的成绩，下列说法正确的是( )
A.小明成绩更稳定
B.小颖成绩更稳定
C.小明、小颖成绩一样稳定
D.无法判断
8.(母题：教材P121习题T1)如图，四边形ABCD是正方形，F是CB延长线上一点，E是CD上一点，若△AFB绕点A按逆时针方向旋转θ度后与△AED重合，则θ的最小值为( )
(第8题)
A.90B.60C.45D.30
9.新能源车的技术越来越成熟，而且更加环保节能，小松同学的爸爸准备换一台车，通过对比两台续航里程相同的燃油车和新能源车，发现燃油车的每千米行驶费用比新能源车多0.54元，已知燃油车的油箱容积为40升，燃油价格为9元/升，新能源车电池容量为60千瓦时，电价为0.6元/千瓦时，则小松爸爸选择的两台汽车的续航里程是( )
A.600 kmB.500 kmC.450 kmD.400 km
10.[2023·人大附中月考]已知－1＜x＜0，点P的坐标为(－3－x，－－x)，点Q的坐标为(0，2 023)，O为坐标原点，则∠POQ满足( )
A.大于135小于180°B.等于135°
C.大于90°小于135°D.大于0°小于90°
二、填空题(每题3分，共24分)
11.已知点P(a，b)在一次函数y＝4x＋3的图象上，则代数式4a－b－2的值等于 .
12.写出一个反比例函数y＝kx(k≠0)，使它的图象在每个象限内，都满足y的值随x值的增大而减小，这个函数的表达式为 .
(第13题)
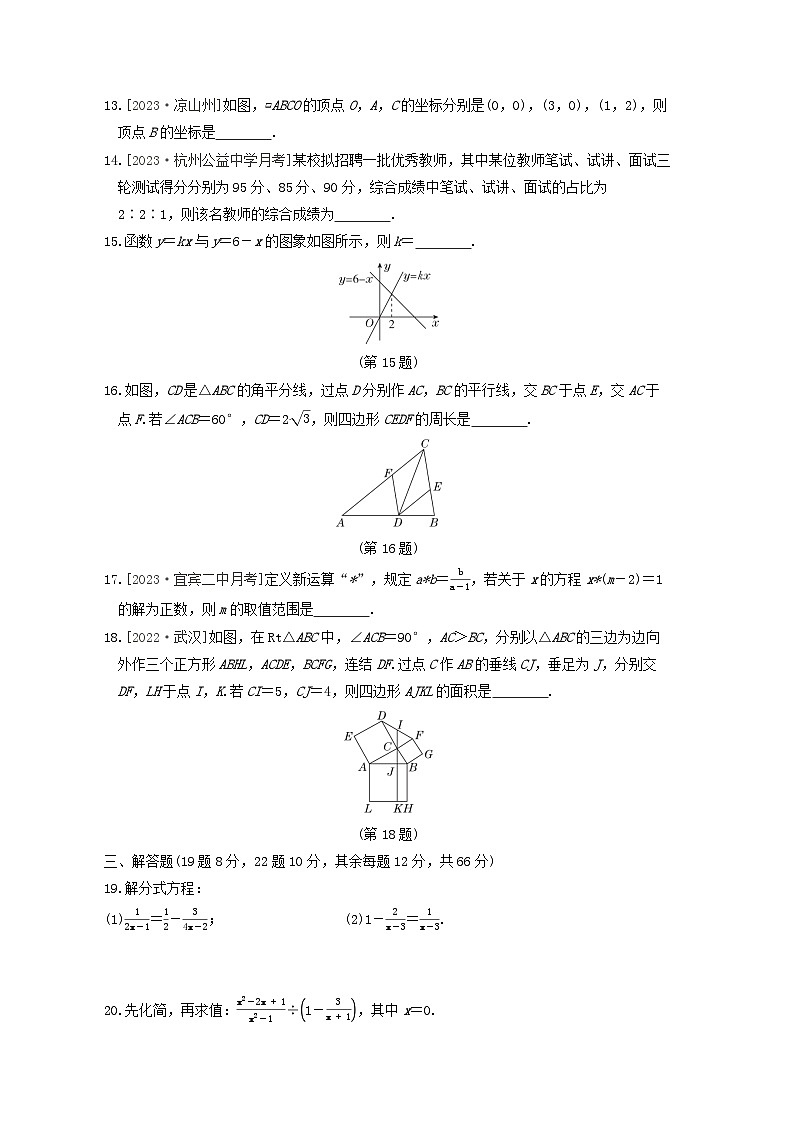
13.[2023·凉山州]如图，▱ABCO的顶点O，A，C的坐标分别是(0，0)，(3，0)，(1，2)，则顶点B的坐标是 .
14.[2023·杭州公益中学月考]某校拟招聘一批优秀教师，其中某位教师笔试、试讲、面试三轮测试得分分别为95分、85分、90分，综合成绩中笔试、试讲、面试的占比为2∶2∶1，则该名教师的综合成绩为 .
15.函数y＝kx与y＝6－x的图象如图所示，则k＝ .
(第15题)
16.如图，CD是△ABC的角平分线，过点D分别作AC，BC的平行线，交BC于点E，交AC于点F.若∠ACB＝60°，CD＝23，则四边形CEDF的周长是 .
(第16题)
17.[2023·宜宾二中月考]定义新运算“*”，规定a*b＝ba－1，若关于x的方程x*(m－2)＝1的解为正数，则m的取值范围是 .
18.[2022·武汉]如图，在Rt△ABC中，∠ACB＝90°，AC＞BC，分别以△ABC的三边为边向外作三个正方形ABHL，ACDE，BCFG，连结DF.过点C作AB的垂线CJ，垂足为J，分别交DF，LH于点I，K.若CI＝5，CJ＝4，则四边形AJKL的面积是 .
(第18题)
三、解答题(19题8分，22题10分，其余每题12分，共66分)
19.解分式方程：
(1)12x－1＝12－34x－2；(2)1－2x－3＝1x－3.
20.先化简，再求值：x2－2x+1x2－1÷1－3x+1，其中x＝0.
21.[2023·驻马店二中模拟]如图，在平面直角坐标系中，一次函数y＝x＋2的图象与反比例函数y＝kx(x＞0)的图象交于点A(1，m)，与x轴交于点C.
(1)求反比例函数的表达式；
(2)B是反比例函数图象上一点，且纵坐标是1，BD∥x轴，交直线AC于点D，求BD的长.
22.[2023·苏州]某初中学校为加强劳动教育，开设了劳动技能培训课程.为了解培训效果，学校对七年级320名学生在培训前和培训后各进行一次劳动技能检测，两次检测项目相同，评委依据同一标准进行现场评估，分成“合格”“良好”“优秀”3个等级，依次记为2分、6分、8分(比如，某同学检测等级为“优秀”，即得8分).学校随机抽取32名学生的两次检测等级作为样本，绘制成如图所示的条形统计图.
(1)这32名学生在培训前得分的中位数对应等级应为 .(填“合格”“良好”或”优秀”)；
(2)求这32名学生培训后比培训前的平均分提高了多少；
(3)利用样本估计该校七年级学生中，培训后检测等级为“良好”与“优秀”的学生人数之和是多少？
23.如图，在矩形ABCD中，AB＝3 cm，BC＝4 cm，E，F是对角线AC上的两个动点，分别从A，C同时出发相向而行，速度均为1 cm/s，运动时间为t s，0≤t≤5.
(1)AE＝ cm，EF＝ cm；
(2)若G，H分别是AB，DC的中点，求证：四边形EGFH是平行四边形；
(3)在(2)的条件下，当t为何值时，四边形EGFH为矩形？
24.党的二十大报告中指出，推动能源清洁低碳高效利用，推进工业、建筑、交通等领域清洁低碳转型，深入推进能源革命，某市交通管理局决定购买一批电动公交车取代燃油公交车.根据调查发现，购买A型电动公交车2辆、B型电动公交车1辆，共需资金112万元；购买A型电动公交车1辆、B型电动公交车1辆，共需资金76万元.
(1)求A、B两种型号的电动公交车的单价分别是多少万元.
(2)该交通管理局计划出资1 128万元，准备购买这两种电动公交车共30辆，其中A型电动公交车的数量不多于20辆，请你设计出最省钱的购买方案.
答案
一、1.A 2.C
3.D 【点拨】根据平行四边形对角线互相平分的性质即可求出AO的长度，根据勾股定理求出BO，最后求出BD即可.
4.C 【点拨】分k＞0和k＜0讨论直线和双曲线在坐标系中的位置即可.
5.C
6.D 【点拨】∵－2＜0，∴当x1＜x2时，y1＞y2，A正确；画图象可知B正确；y＝－2x＋4的图象向下平移4个单位得y＝－2x＋4－4＝－2x的图象，C正确；令y＝0，x＝2，则函数图象与x轴的交点坐标是(2， 0)，D错误.
7.B 8.A
9.A 【点拨】设续航里程为x km，由题意可列方程40×9x＝60×0.6x＋0.54，解得x＝600.
10.C 【点拨】先判断出－3－x＜0，－－x＜0，则点P在第三象限，再证明3－x＞－x，即点P到y轴的距离大于点P到x轴的距离，则点P在第三象限的平分线的上方，且在x轴的下方，由此即可得到答案.
二、11.－5 12.y＝3x(答案不唯一)
13.(4，2)【点拨】如图，延长BC交y轴于点D.
∵四边形ABCO是平行四边形，
∴BC＝OA，BC∥OA.
∵OA⊥y轴，∴BC⊥y轴.
∵A(3，0)，C(1，2)，
∴BC＝OA＝3，CD＝1，OD＝2，
∴BD＝CD＋BC＝1＋3＝4.∴B(4，2).
14.90分 15.2 16.8
17.m＞1且m≠2 【点拨】根据题意知a*b＝ba－1.
∵x*(m－2)＝1，∴m－2x－1＝1，解得x＝m－1，
又∵x*(m－2)＝1的解为正数，且x－1≠0，
∴m－1>0，m－1－1≠0，解得m＞1且m≠2.
18.80 【点拨】由题易知△DCF≌△ACB，∴∠CDF＝∠BAC，
∵∠BCJ＋∠CBA＝90°＝∠BAC＋∠CBA，∴∠BCJ＝∠BAC，
∴∠BCJ＝∠CDI，又∵∠BCJ＝∠ICD，∴∠CDI＝∠ICD，∴DI＝CI，
同理可得CI＝IF，∴I为斜边DF中点，
DF＝2CI＝2×5＝10＝AB.
取AB中点Q，连结CQ，则易得CQ＝AQ＝5，∵CJ＝4，∴QJ＝3，
∴AJ＝AQ＋QJ＝8，∴四边形AJKL的面积为8×10＝80.
三、19.【解】(1)方程两边同时乘以2(2x－1)，
得2＝2x－1－3.
化简，得2x＝6.解得x＝3.
检验：当x＝3时，2(2x－1)＝2×(2×3－1)＝10≠0，
所以x＝3是原方程的解.
(2)方程两边同时乘以(x－3)，得x－3－2＝1.解得x＝6.
检验：当x＝6时，x－3＝6－3＝3≠0，
所以x＝6是原方程的解.
20.【解】原式＝(x－1)2(x+1)(x－1)÷(x+1x+1－3x+1)＝(x－1)2(x+1)(x－1)·x+1x－2＝x－1x－2.
当x＝0时，原式＝12.
21.【解】(1)∵一次函数y＝x＋2的图象过点A(1，m)，
∴m＝1＋2＝3，∴A(1，3) .
∵点A在反比例函数y＝kx(x＞0)的图象上，
∴k＝1×3＝3，
∴反比例函数的表达式为y＝3x.
(2)∵点B是反比例函数图象上一点且纵坐标是1，
当y＝1时，1＝3x，解得x＝3，
∴B(3，1) .
∵BD∥x轴，交直线AC于点D，
∴D点的纵坐标为1，
代入y＝x＋2，得1＝x＋2，
解得x＝－1.
∴D(－1，1)，∴BD＝3－(－1)＝4.
22.【解】(1)合格
(2)培训前的平均分为(25×2＋5×6＋2×8)÷32＝3(分)；
培训后的平均分为(8×2＋16×6＋8×8)÷32＝5.5(分).
5.5－3＝2.5(分)，培训后比培训前的平均分提高了2.5分.
(3)样本中培训后“良好”的比例为1632＝12＝0.50；样本中培训后“优秀”的比例为832＝14＝0.25.
∴培训后检测等级为“良好”与“优秀”的学生共有320×(0.5＋0.25)＝240(名).
23.(1)t；(5－2t)或(2t－5)
(2)【证明】∵四边形ABCD是矩形，
∴AB＝CD，AB∥CD，∠B＝90°.
∴AC＝AB2＋BC2＝32＋42＝5(cm)，
∠GAF＝∠HCE.
∵G，H分别是AB，DC的中点，
∴AG＝12AB，CH＝12CD.∴AG＝CH.
易知AE＝CF，∴AF＝CE.
∴△AFG≌△CEH.∴GF＝HE.
同理，GE＝HF.
∴四边形EGFH是平行四边形.
(3)【解】如图，连结GH.
由点G，H分别是矩形ABCD的边AB，DC的中点，
易知GH＝BC＝4 cm.
由(2)可知四边形EGFH是平行四边形，
∴当EF＝GH＝4 cm时，四边形EGFH是矩形.分两种情况：
①当AE＝CF＝t cm，EF＝(5－2t)cm时，5－2t＝4，
解得t＝0.5.
②当AE＝CF＝t cm，EF＝(2t－5)cm时，2t－5＝4，
解得t＝4.5.
∴当t为0.5或4.5时，四边形EGFH为矩形.
24.【解】设A型电动公交车的单价为x万元，B型电动公交车的单价为y万元.
依题意，得2x＋y=112，x＋y=76，解得x=36，y=40.
答：A型电动公交车的单价是36万元，B型电动公交车的单价是40万元.
(2)设购买A型电动公交车m辆，则购买B型电动公交车(30－m)辆.
依题意，得36m＋40(30－m)≤1 128，解得m≥18.
又∵m≤20，∴18≤m≤20.
设购买这两种电动公交车共30辆的总费用为w万元，
依题意，得w＝36m＋40(30－m)＝－4m＋1 200.
∵－4＜0，∴w随m的增大而减小.
∴当m＝20时，w取得最小值，此时30－m＝30－20＝10.
∴最省钱的购买方案为购买A型电动公交车20辆，B型电动公交车10辆.