2024年广东省茂名市高州市第一中学附属实验中学九年级中考一模数学试题

这是一份2024年广东省茂名市高州市第一中学附属实验中学九年级中考一模数学试题，共12页。试卷主要包含了实数9的相反数等于，下列运算正确的是等内容，欢迎下载使用。

（满分为120分，考试时间为120分钟）
一．选择题（本大题共10小题，每小题3分，共30分）
1．实数9的相反数等于（ ）
A．﹣9 B．+9 C． D．﹣
2．277000000用科学记数法表示为（ ）
A．277×106 B．2.77×107 C．2.8×108 D．2.77×108
3．下列运算正确的是（ ）
A．2﹣＝2 B．（a+1）2＝a2+1C．（a2）3＝a5 D．2a2•a＝2a3
4．下列图形中既是轴对称图形又是中心对称图形的是（ ）
A． B．C． D．
5．某种商品原来每件售价为150元，经过连续两次降价后，该种商品每件售价为96元，设平均每次降价的百分率为x，根据题意，所列方程正确的是（ ）
A．150（1﹣x2）＝96 B．150（1﹣x）＝96 C．150（1﹣x）2＝96 D．150（1﹣2x）＝96
6．若关于x的一元二次方程x2+x+m＝0有两个相等的实数根，则实数m的值为（ ）
A．﹣4B．﹣C．D．4
7．不透明的袋子中装有红、绿小球各一个，除颜色外两个小球无其他差别．从中随机摸出一个小球，放回并摇匀，再从中随机摸出一个小球，那么第一次摸到红球、第二次摸到绿球的概率是（ ）
A．B．C． D．
8．如图，OA，OB是⊙O的两条半径，点C在⊙O上，若∠AOB＝80°，
则∠C的度数为（ ）
A．30°B．40°C．50° D．60°
9．一个多边形的内角和为900°，则这个多边形是（ ）
A．七边形B．八边形 C．九边形 D．十边形
10．如图，在平面直角坐标系中，边长为2的正六边形ABCDEF的中心与
原点O重合，AB∥x轴，交y轴于点P．将△OAP绕点O顺时针旋转，
每次旋转90°，则第2024次旋转结束时，点A的坐标为（ ）
A．（，﹣1）B．（﹣1，﹣） C．（﹣，﹣1） D．（1，）
二．填空题(本大题共5小题，每小题3分, 共15分)
11．分解因式：xy2﹣x＝ ．
12．已知点A（﹣2，b）与点B（a，3）关于原点对称，则a﹣b＝ ．
13．已知反比例函数y＝﹣的图象经过点（4，a），则a的值为 ．
14．如图，△ABC中，点D、E分别是AB、AC的中点，若S△ADE＝2，则S△ABC＝ ．
15．如图，在矩形纸片ABCD中，点E在BC边上，将△CDE沿DE翻折得到
△FDE，点F落在AE上．若CE＝3cm，AF＝2EF，则AB＝ cm．
三、解答题（一）（本大题共3小题，每小题6分，共18分）
16．计算：（π﹣1）0+4sin45°﹣+|﹣3|．
17. 解不等式组 ．
18. 先化简，再求值：（1+）÷，其中a＝+1．
四、解答题（二）（本大题共3小题，每小题7分，共21分）
19. 如图，在▱ABCD中，AC，BD交于点O，点E，F在AC上，AE＝CF．
（1）求证：四边形EBFD是平行四边形；
（2）若∠BAC＝∠DAC，求证：四边形EBFD是菱形．
20. 如图，点A在反比例函数y＝（x＞0）的图象上，AB⊥x轴，垂足为B（3，0），过C（5，0）作CD⊥x轴，交过B点的一次函数y＝x+b的图象于D点，交反比例函数的图象于E点，S△AOB＝3．
（1）求反比例比数y＝（x＞0）和一次函数y＝x+b的表达式；
（2）求DE的长．
21. 某班去革命老区研学旅行，研学基地有甲乙两种快餐可供选择，买1份甲种快餐和2份乙种快餐共需70元，买2份甲种快餐和3份乙种快餐共需120元．
（1）买一份甲种快餐和一份乙种快餐各需多少元？
（2）已知该班共买55份甲乙两种快餐，所花快餐费不超过1280元，问至少买乙种快餐多少份？
五．解答题（三）（本大题共2小题，每小题8分，共16分）
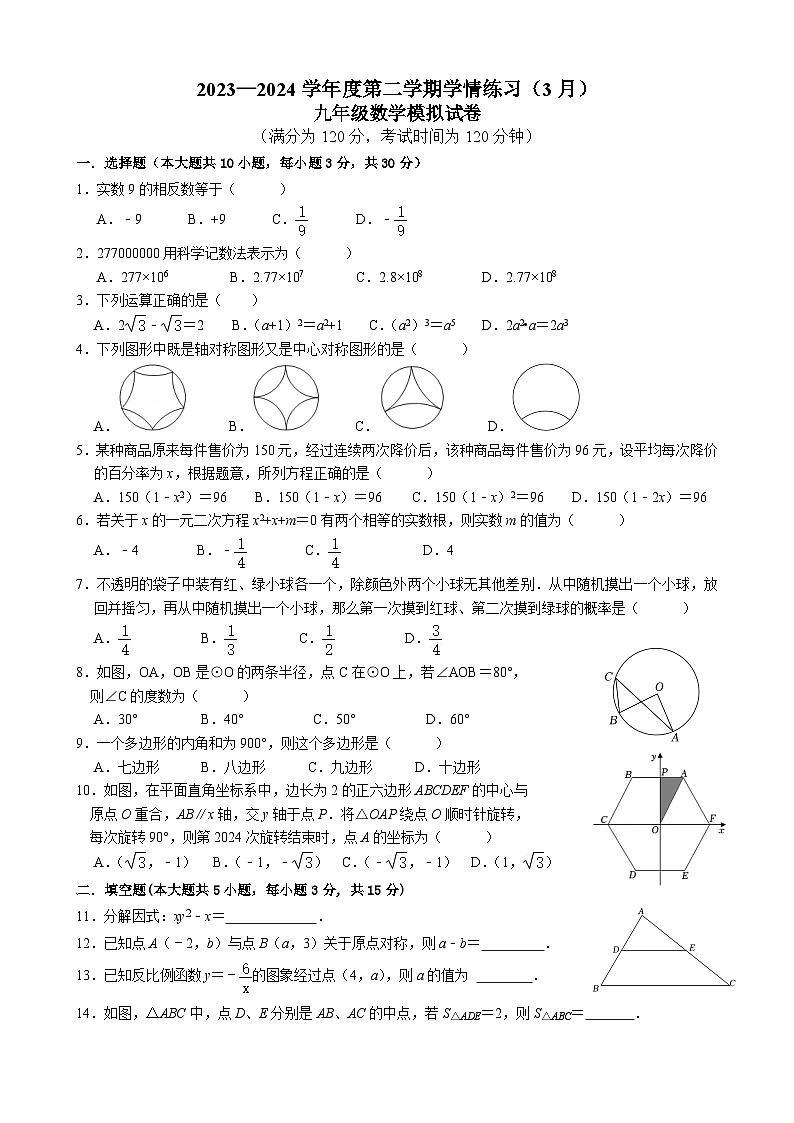
22. 为落实“双减”政策，优化作业管理，某中学从全体学生中随机抽取部分学生，调查他们每天完成书面作业的时间t（单位：分钟）．按照完成时间分成五组：A组“t≤45”，B组“45＜t≤60”，C组“60＜t≤75”，D组“75＜t≤90”，E组“t＞90”．将收集的数据整理后，绘制成如下两幅不完整的统计图．
根据以上信息，解答下列问题：
（1）这次调查的样本容量是 ，请补全条形统计图；
（2）在扇形统计图中，B组的圆心角是 度，本次调查数据的中位数落在 组内；
（3）若该校有1800名学生，请你估计该校每天完成书面作业不超过90分钟的学生人数．
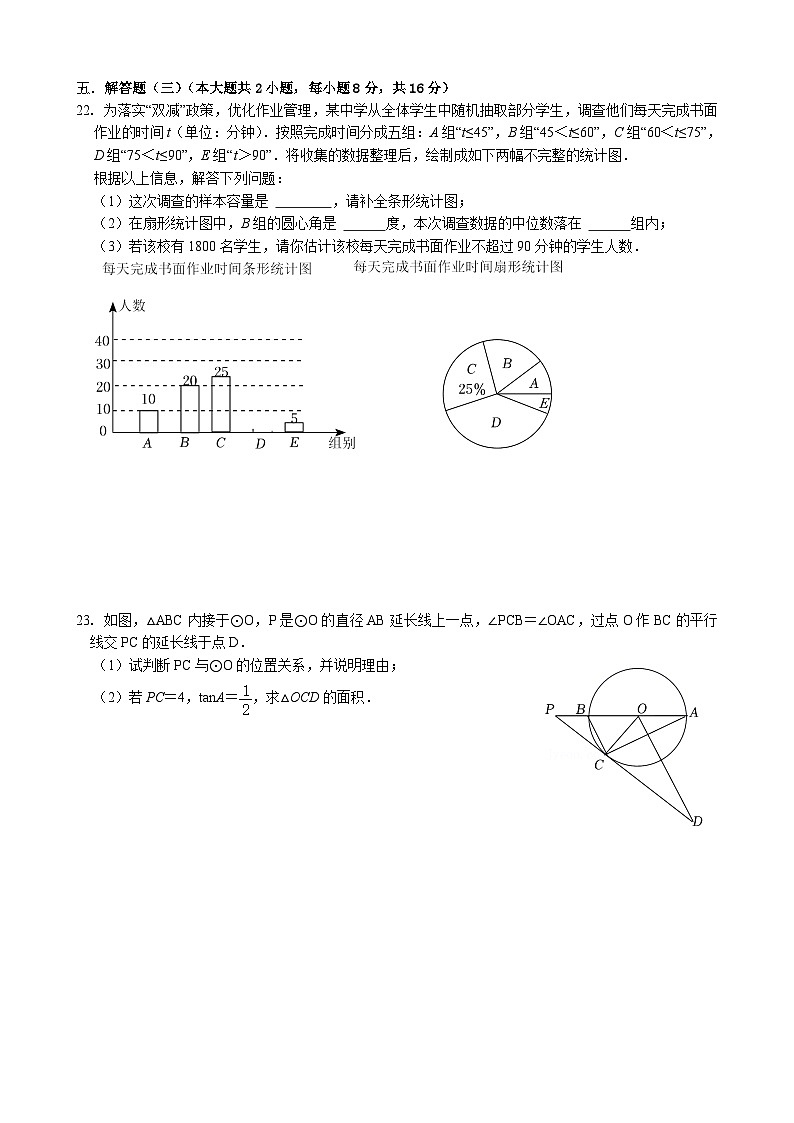
23. 如图，△ABC内接于⊙O，P是⊙O的直径AB延长线上一点，∠PCB＝∠OAC，过点O作BC的平行线交PC的延长线于点D．
（1）试判断PC与⊙O的位置关系，并说明理由；
（2）若PC＝4，tanA＝，求△OCD的面积．
六．解答题（四）（本大题共2小题，每小题10分，共20分）
24. 如图1，在平面直角坐标系中，抛物线y＝（x+3）（x﹣a）与x轴交于A，B（4，0）两点，点C在y轴上，且OC＝OB，D，E分别是线段AC，AB上的动点（点D，E不与点A，B，C重合）．
（1）求此抛物线的表达式；
（2）连接DE并延长交抛物线于点P，当DE⊥x轴，且AE＝1时，求DP的长；
（3）连接BD．
①如图2，将△BCD沿x轴翻折得到△BFG，当点G在抛物线上时，求点G的坐标；
②如图3，连接CE，当CD＝AE时，求BD+CE的最小值．
25. 综合与实践
【问题情境】：
数学活动课上，老师出示了一个问题：如图1，在正方形ABCD中，E是BC的中点，AE⊥EP，EP与正方形的外角∠DCG的平分线交于P点．试猜想AE与EP的数量关系，并加以证明；
【思考尝试】：
（1）同学们发现，取AB的中点F，连接EF可以解决这个问题．请在图1中补全图形，解答老师提出的问题．
【实践探究】：
（2）希望小组受此问题启发，逆向思考这个题目，并提出新的问题：如图2，在正方形ABCD中，E为BC边上一动点（点E，B不重合），△AEP是等腰直角三角形，∠AEP＝90°，连接CP，可以求出∠DCP的大小，请你思考并解答这个问题．
【拓展迁移】：
（3）突击小组深入研究希望小组提出的这个问题，发现并提出新的探究点：如图3，在正方形ABCD中，E为BC边上一动点（点E，B不重合），△AEP是等腰直角三角形，∠AEP＝90°，连接DP．知道正方形的边长时，可以求出△ADP周长的最小值．当AB＝4时，请你求出△ADP周长的最小值．
2023—2024学年度第二学期学情练习（3月）九年级数学试卷答案
一．选择题（本大题共10小题，每小题3分，共30分）
1．A 2．D 3．D 4．B 5．C 6．C 7．A 8．B 9．A 10．D
二．填空题(本大题共5小题，每小题3分, 共15分)
11．x（y﹣1）（y+1）； 12．5； 13．﹣； 14．8； 15．3；
三、解答题（一）（本大题共3小题，每小题6分，共18分）
16、原式＝1+4×﹣2+3
＝1+2﹣2+3
＝4．
17、解：，
解不等式①，得：x＞2，
解不等式②，得：x≤3，
∴原不等式组的解集是2＜x≤3．
18、解：原式＝÷
＝•
＝，
当a＝+1时，原式＝＝．
四、解答题（二）（本大题共3小题，每小题7分，共21分）
19、证明：（1）在▱ABCD中，OA＝OC，OB＝OD，
∵AE＝CF．
∴OE＝OF，
∴四边形EBFD是平行四边形；
（2）∵四边形ABCD是平行四边形，
∴AB∥DC，
∴∠BAC＝∠DCA，
∵∠BAC＝∠DAC，
∴∠DCA＝∠DAC，
∴DA＝DC，
∵OA＝OC，
∴DB⊥EF，
∴平行四边形EBFD是菱形．．
20、解：（1）∵点A在反比例函数y＝（x＞0）的图象上，AB⊥x轴，
∴S△AOB＝|k|＝3，
∴k＝6，
∴反比例函数为y＝，
∵一次函数y＝x+b的图象过点B（3，0），
∴×3+b＝0，解得b＝﹣，
∴一次函数为y＝x﹣；
（2）∵过C（5，0）作CD⊥x轴，交过B点的一次函数y＝x+b的图象于D点，
∴当x＝5时y＝＝；y＝x﹣＝3，
∴E（5，），D（5，3），
∴DE＝3﹣＝．
21、解：（1）设购买一份甲种快餐需要x元，购买一份乙种快餐需要y元，
依题意得：，
解得：．
答：购买一份甲种快餐需要30元，购买一份乙种快餐需要20元．
（2）设购买乙种快餐m份，则购买甲种快餐（55﹣m）份，
依题意得：30（55﹣m）+20m≤1280，
解得：m≥37．
答：至少买乙种快餐37份．
五．解答题（三）（本大题共2小题，每小题8分，共16分）
22、解：（1）这次调查的样本容量是：25÷25%＝100，
D组的人数为：100﹣10﹣20﹣25﹣5＝40，
补全的条形统计图如右图所示：
故答案为：100；
（2）在扇形统计图中，B组的圆心角是：360°×＝72°，
∵本次调查了100个数据，第50个数据和51个数据都在C组，
∴中位数落在C组， 故答案为：72，C；
（3）1800×＝1710（人），
答：估计该校每天完成书面作业不超过90分钟的学生有1710人．
23、解：（1）PC是⊙O的切线，理由如下：
∵AB是⊙O的直径，
∴∠ACB＝90°，
∴∠OAC+∠OBC＝90°，
∵OB＝OC，
∴∠OBC＝∠OCB，
∵∠PCB＝∠OAC，
∴∠PCB+∠OCB＝90°，
∴∠PCO＝90°，即OC⊥PC，
∵OC是半径，
∴PC是⊙O的切线；
（2）在Rt△ACB中，tanA＝，
∵tanA＝，
∴＝，
∵∠PCB＝∠OAC，∠P＝∠P，
∴△PCB∽△PAC，
∴＝＝＝，
∵PC＝4，
∴PB＝2，PA＝8，
∴AB＝PA﹣PB＝8﹣2＝6，
∴OC＝OB＝OA＝3，
∵BC∥OD，
∴，即，
∴CD＝6，
∵OC⊥CD，
∴＝×3×6＝9．
六．解答题（四）（本大题共2小题，每小题10分，共20分）
24、解：（1）∵抛物线y＝（x+3）（x﹣a）与x轴交于A，B（4，0）两点，
∴（4+3）（4﹣a）＝0，
解得a＝4，
∴y＝（x+3）（x﹣4）＝x2﹣x﹣3，
即抛物线的表达式为y＝x2﹣x﹣3；
（2）在y＝（x+3）（x﹣4）中，令y＝0，得x＝﹣3或4，
∴A（﹣3，0），OA＝3，
∵OC＝OB＝4，
∴C（0，4），
∵AE＝1，
∴DE＝AE•tan∠CAO＝AE＝，OE＝OA﹣AE＝3﹣1＝2，
∴E（﹣2，0），
∵DE⊥x轴，
∴xP＝xD＝xE＝﹣2，
∴yP＝（﹣2+3）（﹣2﹣4）＝﹣，
∴PE＝，
∴DP＝DE+PE＝+＝；
（3）①如下图，连接DG交AB于点M，
∵△BCD与BFG关于x轴对称，
∴DG⊥AB，DM＝GM，
设OM＝a（a＞0），则AM＝OA﹣OM＝3﹣a，
MG＝MD＝AM•tan∠CAO＝（3﹣a），
∴G（﹣a，（a﹣3）），
∵点G（﹣a，（a﹣3））在抛物线y＝（x+3）（x﹣4）上，
∴（﹣a+3）（﹣a﹣4）＝（a﹣3），
解得a＝或3（舍去），
∴G（﹣，﹣）；
②如下图，在AB的下方作∠EAQ＝∠DCB，且AQ＝BC，连接EQ，CQ，
∵AE＝CD，
∴△AEQ≌△CDB（SAS），
∴EQ＝BD，
∴当C、E、Q三点共线时，BD+CE＝EQ+CE最小，最小为CQ，
过点C作CH⊥AQ，垂足为H，
∵OC⊥OB，OC＝OB＝4，
∴∠CBA＝45°，BC＝4，
∵∠CAH＝180°﹣∠CAB﹣∠EAQ＝180°﹣∠CAB﹣∠DCB＝∠CBA＝45°，
AC＝＝＝5，AH＝CH＝AC＝，
HQ＝AH+AQ＝AH+BC＝＝，
∴CQ＝＝＝，
即BD+CE的最小值为；
方法二：过点C作CF∥x轴，使得CF＝AC，作BG⊥FC延长线于点G，
∴∠FCA＝∠CAE，
又∵CD＝AE，CF＝AC，
∴△FCD≌△CAE（SAS），
∴FD＝CE，
∴F、D、B三点共线时CE+BD＝FD+BD取到最小值，
∵AC＝5，C（0，4），B（4，0），
∴BF的长＝＝．
25、解：（1）AE＝EP，
理由如下：取AB的中点F，连接EF，
∵F、E分别为AB、BC的中点，
∴AB＝BF＝BE＝CE，
∴∠BFE＝45°，
∴∠AFE＝135°，
∵CP平分∠DCG，
∴∠DCP＝45°，
∴∠ECP＝135°，
∴∠AFE＝∠ECP，
∵AE⊥PE，
∴∠AEP＝90°，
∴∠AEB+∠PEC＝90°，
∵∠AEB+∠BAE＝90°，
∴∠PEC＝∠BAE，
∴△AFE≌△ECP（ASA），
∴AE＝EP；
（2）在AB上取AF＝EC，连接EF，
由（1）同理可得∠CEP＝∠FAE，
∵AF＝EC，AE＝EP，
∴△FAE≌△CEP（SAS），
∴∠ECP＝∠AFE，
∵AF＝EC，AB＝BC，
∴BF＝BE，
∴∠BEF＝∠BFE＝45°，
∴∠AFE＝135°，
∴∠ECP＝135°，
∴∠DCP＝45°，
（3）作DG⊥CP，交BC的延长线于G，交CP于O，连接AG，
由（2）知，∠DCP＝45°，
∴∠CDG＝45°，
∴△DCG是等腰直角三角形，
∴点D与G关于CP对称，
∴AP+DP的最小值为AG的长，
∵AB＝4，
∴BG＝8，
由勾股定理得AG＝4，
∴△ADP周长的最小值为AD+AG＝4+4．