“8+4+4”小题强化训练（10）-2024届高三数学二轮复习《8+4+4》小题强化训练（新高考地区专用）

这是一份“8+4+4”小题强化训练（10）-2024届高三数学二轮复习《8+4+4》小题强化训练（新高考地区专用），文件包含“8+4+4”小题强化训练10新高考地区专用原卷版docx、“8+4+4”小题强化训练10新高考地区专用解析版docx等2份试卷配套教学资源，其中试卷共17页， 欢迎下载使用。
一、注意基础知识的整合、巩固。二轮复习要注意回归课本，课本是考试内容的载体，是高考命题的依据。浓缩课本知识，进一步夯实基础，提高解题的准确性和速度
二、查漏补缺，保强攻弱。在二轮复习中，对自己的薄弱环节要加强学习，平衡发展，加强各章节知识之间的横向联系，针对“一模”考试中的问题要很好的解决，根据自己的实际情况作出合理的安排。
三、提高运算能力，规范解答过程。在高考中运算占很大比例，一定要重视运算技巧粗中有细，提高运算准确性和速度，同时，要规范解答过程及书写。
四、强化数学思维，构建知识体系。同学们在听课时注意把重点要放到理解老师对问题思路的分析以及解法的归纳总结，以便于同学们在刷题时做到思路清晰，迅速准确。
五、解题快慢结合，改错反思。审题制定解题方案要慢，不要急于解题，要适当地选择好的方案，一旦方法选定，解题动作要快要自信。
六、重视和加强选择题的训练和研究。对于选择题不但要答案正确，还要优化解题过程，提高速度。灵活运用特值法、排除法、数形结合法、估算法等。

2024届高三二轮复习“8+4+4”小题强化训练(10)
一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．若集合，则（ ）
A. B.
C. D.
【答案】C
【解析】，
故.
故选：C
2．设，若复数在复平面内对应的点位于虚轴上，则（ ）
A. B. C. D.
【答案】B
【解析】根据题意可得，
所以在复平面内对应的点为，即在虚轴上，
因此可得，即；
故选：B
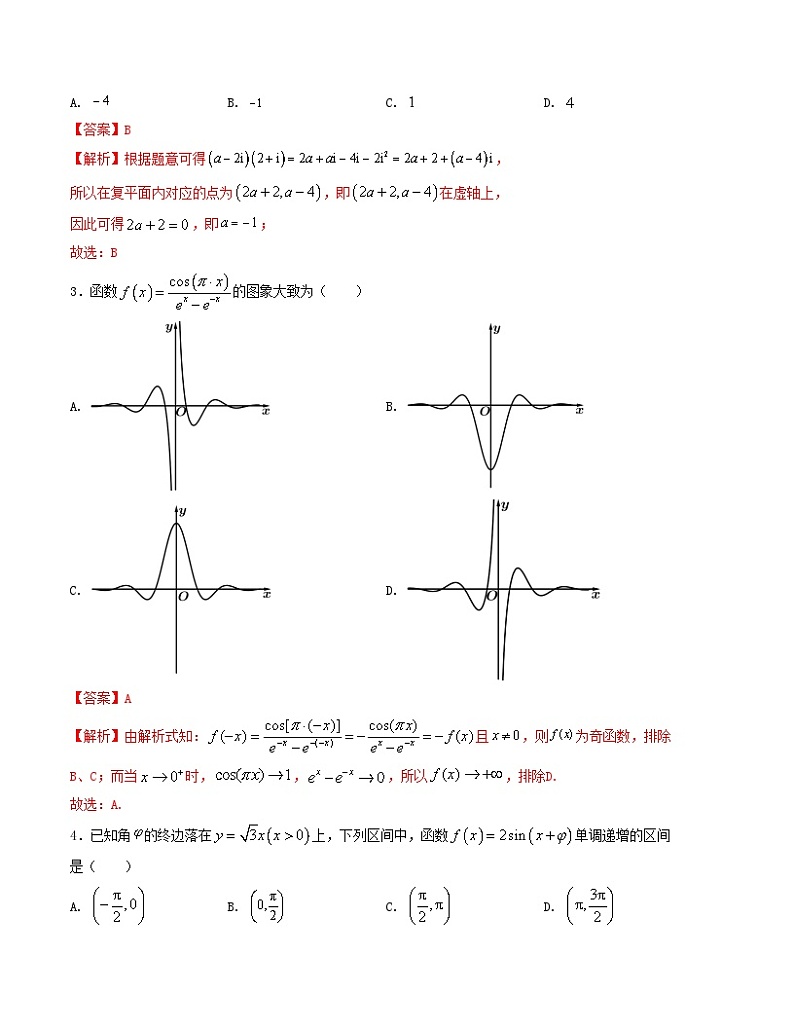
3．函数的图象大致为（ ）
A. B.
C. D.
【答案】A
【解析】由解析式知：且，则为奇函数，排除B、C；而当时，，，所以，排除D.
故选：A.
4．已知角的终边落在上，下列区间中，函数单调递增的区间是（ ）
A. B. C. D.
【答案】A
【解析】因为角的终边落在上，
可取一点，
则，则与的终边相同，
可令，
则，
令,
所以，
所以的单调递增区间为
，
只有，故A正确，B,C,D错误，
故选：A.
5．某校4个班级学生的一次物理考试成绩的频率分布直方图如下，已知成绩在范围内的人数为30人，则下列说法正确的是（ ）
A. 的值为0.15B. 4个班的总人数为210人
C. 学生成绩的中位数估计为66.6分D. 学生成绩的平均数估计为71分
【答案】D
【解析】对A，，解得，故A错误；
对B，成绩在范围内的频率为，故4个班的总人数为人，故B错误；
对C，因为，故学生成绩中位数估计为70分，故C错误；
对D，学生成绩的平均数估计为
分，故D正确.
故选：D
6．已知，，，，则（ ）
A. B. C. D.
【答案】C
【解析】因为，，所以，，
又因为，所以，
所以，
①+②得，②-①得，
上述两式相除即可得，则，
故选：C.
7．已知双曲线C：的左、右焦点分别为，，点P是C上的一点，，的平分线与x轴交于点A，记，的面积分别为，，且，则C的离心率为（ ）
A. B. C. D. 3
【答案】B
【解析】因为，则，可得，
由题意知是的平分线，所以，
又，所以，则，
所以，整理得，故，得，即，
所以.
故选：B.
8．在数列中的相邻两项与之间插入一个首项为，公差为的等差数列的前项，记构成的新数列为，若，则前65项的和为（ ）
A. B. -13C. D. -14
【答案】A
【解析】数列为：，
，
设及其后面项的和为，则，
所以数列是以1为首项，公差为的等差数列.
所以前65项的和为，
故选：A.
二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．
9．下列函数中最小值为2的是（ ）
A. B.
C. D.
【答案】AB
【解析】由题意，
A项，，故A正确；
B项，在中，，所以，当且仅当时，等号成立，故B正确；
C项，，，故，当且仅当即时等号成立，C错误；
D项，，，只有当时才有，当且仅当即时等号成立，故D错误.
故选：AB
10．已知圆O：与圆C：交于A，B两点，则下列说法正确的是（ ）
A. 线段AB的垂直平分线所在的直线方程为
B. 直线AB的方程为
C.
D. 若点P是圆O上的一点，则△PAB面积的最大值为
【答案】ABD
【解析】由圆C：知圆心为，
所以直线OC的方程为，即，
所以线段AB的垂直平分线所在的直线方程为，故A正确；
因为圆O：与圆C：，两圆方程作差，
可得直线AB的方程为，故B正确；
点O到直线AB的距离，所以，故C错误；
点到直线的距离的最大值为，则面积的最大值为，故D正确．
故选：ABD．
11．已知是定义在R上的函数，且不恒为0，为奇函数，为偶函数，为的导函数，则（ ）
A. B.
C. 的图象关于直线对称 D.
【答案】ABD
【解析】为奇函数，则的图象关于对称.
又为偶函数，则的图象关于直线对称，
所以，可得
，
则的周期为4，
对A，，令得，故A选项正确；
对B，又，则的图象关于对称，则，
，令，则，故B正确；
对C，因为，则的图象关于直线对称，故C错误；
又，所以，
由以上可知，，，
函数的周期为4，则，故D正确.
故选：ABD.
12．在四面体中，，，，，分别是棱，，上的动点，且满足均与面平行，则（ ）
A. 直线与平面所成的角的余弦值为
B. 四面体被平面所截得的截面周长为定值1
C. 三角形的面积的最大值为
D. 四面体的内切球的表面积为
【答案】CD
【解析】对于A，取中点，中点，连接,
由于，故，
而，平面，所以平面，
又平面，所以平面平面，
则即为直线与平面所成的角，
又,而，
故，则,所以，故错误；
对于B，设平面棱的交点为，
因为∥平面且平面,平面平面,
所以∥，
由题意可知，否则，重合，不合题意，
故四边形为梯形，同理可得四边形为梯形，
所以，，又，
所以，所以，
又∥，同理可证∥，则∥，同理可证∥，
则四边形为平行四边形，故四边形的周长为2，
即四面体被平面所截得的截面周长为定值2，故错误；
对于C，因为平面，平面，所以，
而∥，所以，
同理可证∥，所以，结合,
所以，
当且仅当时，等号成立，
即三角形的面积的最大值为，故正确；
对于D，由以上分析可知,
所以，
而平面，，故，
而,
设四面体的内切球的半径为，则
即，解得，
故四面体的内切球的表面积为，故正确.
故选：CD.
三、填空题：本题共4小题，每小题5分，共20分．
13．已知的展开式中常数项为20，则实数m的值为______．
【答案】1
【解析】展开式的通项为，令解得，∴．
∴．
故答案为：1
14.向量，，在正方形网格（每个小正方形的边长为1）中的位置如图所示，若向量与共线，则与夹角的余弦值为______
【答案】##
【解析】建立如图所示平面直角坐标系，
则，，，
所以，
又因为向量与共线，所以，
所以，则，，
所以.
故答案为：.
15.若函数是定义在上的奇函数，且对任意恒成立，则的取值范围为__________．
【答案】
【解析】因为函数是定义在上奇函数，
所以，解得，所以，
又因为，所以，
即对任意恒成立，所以，
所以易得到在上单调递增，
由，得，
即，
因为是定义在上的奇函数，所以，
因为在上单调递增，所以，
即对任意恒成立，
若，则，此时对任意恒成立；
若，则，解得，
综上：的取值范围为．
故答案为：.
16．已知为拋物线的焦点，过点的直线与拋物线交于不同的两点，，拋物线在点处的切线分别为和，若和交于点，则的最小值为__________.
【答案】10
【解析】的焦点为，设直线方程为，.
联立直线与抛物线方程有，则.
又求导可得，故直线方程为.
又，故，同理.
联立可得，解得，代入可得，代入韦达定理可得，故.
故，当且仅当，即时取等号.
故答案为：10