浙教版八年级上册5.2 函数一等奖ppt课件

这是一份浙教版八年级上册5.2 函数一等奖ppt课件，共19页。PPT课件主要包含了满足条件，x取任意实数，x≠0，x≥-1，等号右边是整式，全体实数，等号右边是复合式，000万米3，由“形”定“数”，归纳总结等内容，欢迎下载使用。

能够从函数的各种表示方法中获得相应的信息，运用函数解决简单的实际问题.
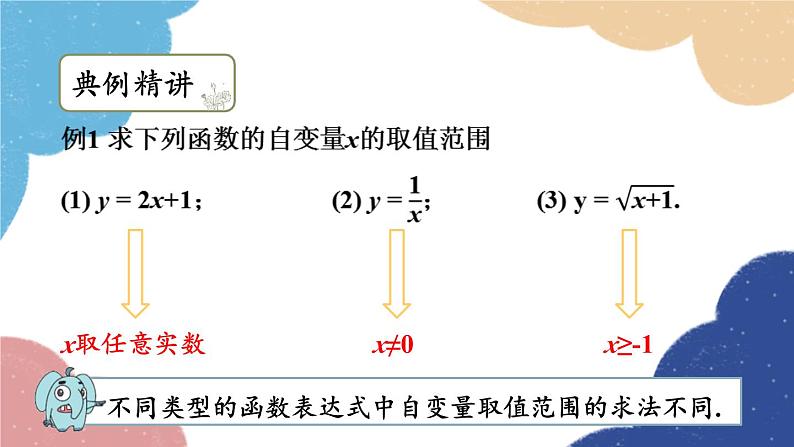
会求简单函数的自变量的取值范围.
一般地，在某个变化过程中，设有两个变量 x 和 y ，如果对于变量 x 的每一个确定的值， y 都有唯一确定的值，那么就说 y 是 x 的函数， x 叫做自变量.
1.还记得常量、变量和函数的定义吗？
在一个变化过程中，固定不变的量叫做常量，可以取不同数值的量叫做变量.
2.请用含自变量的式子表示下列问题中的函数关系：汽车以 60 km/h 的速度匀速行驶，行驶的时间为 t（单位：h），行驶的路程为 s（单位：km）.　
解： s=60t
使函数有意义的自变量取值的全体，叫做函数自变量的取值范围.
（1）必须使含有自变量的代数式有意义；
（2）满足实际问题的意义，如 S = xr2 中，若 r 表示圆的半径，则 r > 0.
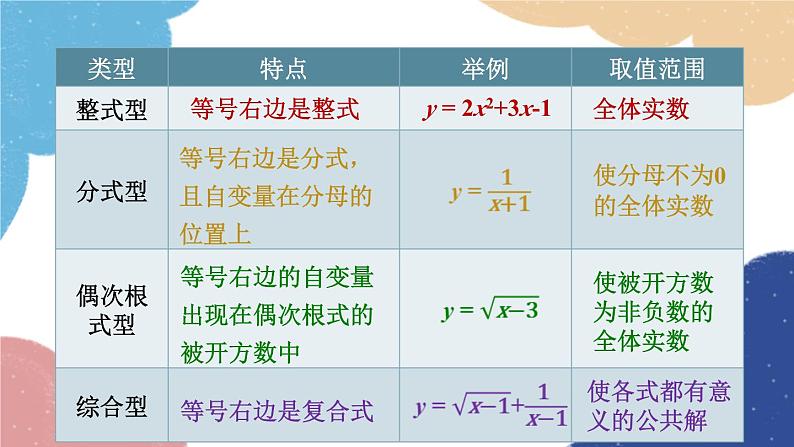
不同类型的函数表达式中自变量取值范围的求法不同.
y = 2x2+3x-1
等号右边是分式，且自变量在分母的位置上
使分母不为0的全体实数
等号右边的自变量出现在偶次根式的被开方数中
使被开方数为非负数的全体实数
使各式都有意义的公共解
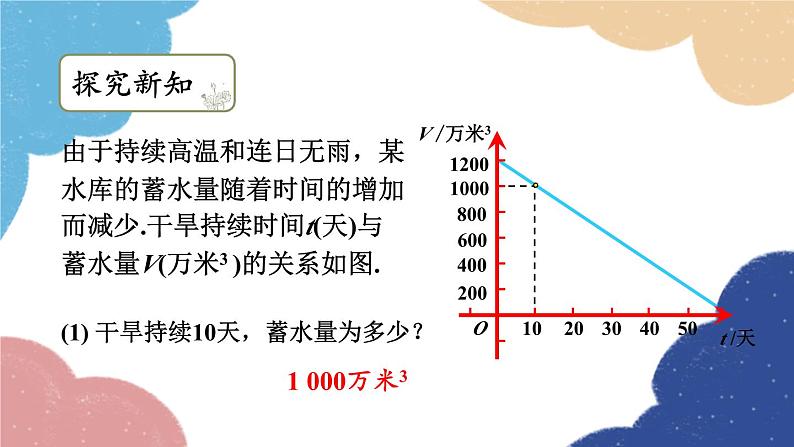
由于持续高温和连日无雨，某水库的蓄水量随着时间的增加而减少.干旱持续时间t(天)与蓄水量V(万米3 )的关系如图.
(1) 干旱持续10天，蓄水量为多少？
(2) 蓄水量小于400万立方米时，将发出严重干旱警报.干旱多少天后将发出严重干旱警报？
1. 理解横、纵坐标分别表示的实际意义.2. 分析已知（看已知的是自变量还是函数值），通过 作x轴或y轴的垂线，在图象上找到对应的点，由点 的横坐标或者纵坐标的值读出要求的值.3. 利用数形结合的思想： 将“数”转化为“形”
如何由函数图象的信息解答实际问题？
例2 一个游泳池内有水300m3，现打开排水管以每小时25m3的排出量排水.
(1) 写出游泳池内剩余水量Q(m3)与排水时间t(h)间的函数表达式；
(2) 写出自变量t的取值范围.
排水后的剩水量Q(m3)是排水时间t(h)的函数，有Q=-25t+300.
池中共有300m3水，每小时排水25m3，故全部排完只需300÷25=12(h)，故自变量t的取值范围是0≤t≤12.
(3) 开始排水后的第5h末，游泳池中还有多少水？
(4) 当游泳池中还剩150m3水时，已经排水多长时间？
当t=5，代入上式得Q=-5×25+300=175（m3）， 即第5h末池中还有水175m3.
当Q=150m3时，由150=-25t+300，得t=6h， 即第6 h末池中有水150m3.
(1)自变量自身表示的意义，如时间、耗油量等不能为负数；(2) 问题中的限制条件.此时多用不等式或不等式组来确定自变量的取值范围.
在实际问题中确定自变量的取值范围，主要考虑两个因素：
解：函数表达式为： y = 50－0.1x.
3. 汽车的油箱中有汽油50L，如果不再加油，那么油箱中的油量 y（单位：L）随行驶里程 x（单位：km）的增加而减少，平均耗油量为0.1L/km.
(1) 写出表示 y 与 x 的函数关系的式子.
(2) 指出自变量x的取值范围；
解：由x≥0及50－0.1x ≥0，得0 ≤ x ≤ 500. 所以自变量x的取值范围是0 ≤ x ≤ 500.
汽车行驶里程，油箱中的油量均不能为负数！
(3) 汽车行驶200km时，油箱中还有多少油？
解：当x=200时，函数y的值为y=50－0.1×200=30.因此，当汽车行驶200 km时，油箱中还有油30L.
如何确定函数自变量的取值范围？
在实际问题中确定自变量的取值范围，主要考虑哪两个因素？