数学八年级上册5.2 函数授课课件ppt

这是一份数学八年级上册5.2 函数授课课件ppt，共27页。PPT课件主要包含了教学目标，m16t，其中x叫做自变量，m是t的函数，t是自变量，s是v的函数，v是自变量，y053x，代一代，查一查等内容，欢迎下载使用。
1.通过实例，了解函数的概念及三种表示法（解析法、列表法、图象法）；2.理解函数值得概念，会在简单情况下根据函数的表示法求函数的值.
通过函数来表示一些实际问题，说明生活离不开数学，数学的发展来源于社会的发展.
初步认识函数的概念，理解函数值的实际意义.
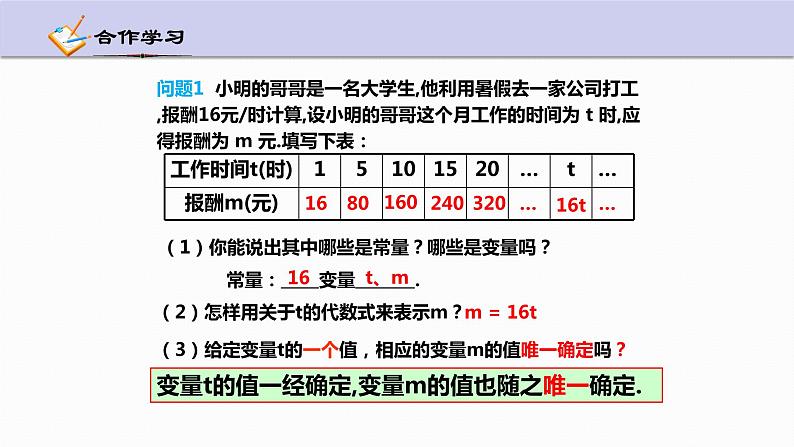
问题1 小明的哥哥是一名大学生,他利用暑假去一家公司打工,报酬16元/时计算,设小明的哥哥这个月工作的时间为 t 时,应得报酬为 m 元.填写下表：
（2）怎样用关于t的代数式来表示m？
（1）你能说出其中哪些是常量？哪些是变量吗？
（3）给定变量t的一个值，相应的变量m的值唯一确定吗？
常量： 变量 .
变量t的值一经确定,变量m的值也随之唯一确定.
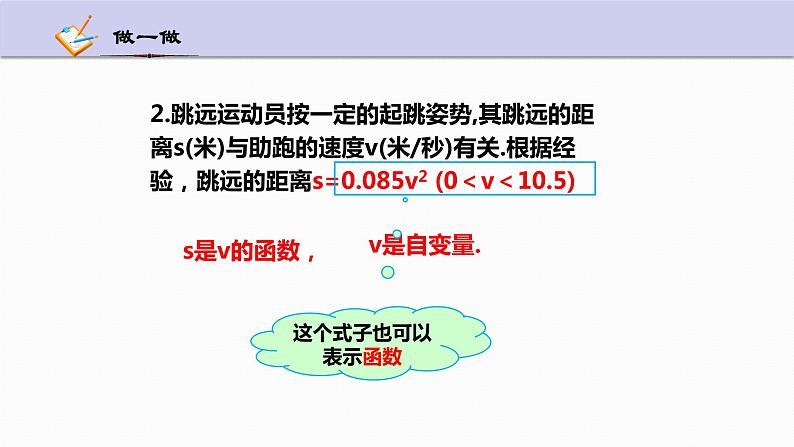
问题2 跳远运动员按一定的起跳姿势,其跳远的距离s(米)与助跑的速度v(米/秒)有关.根据经验,跳远的距离 s = 0.085v2 (0＜v＜10.5)
(2）计算当v分别为7.5, 8, 8.5时,相应的跳远距离S是多少?(结果保留3个有效数字)
(3) 给定一个v的值，你能求出相应的S的值吗?
常量： 变量 .
变量v的值一经确定,变量s的值也随之唯一确定.
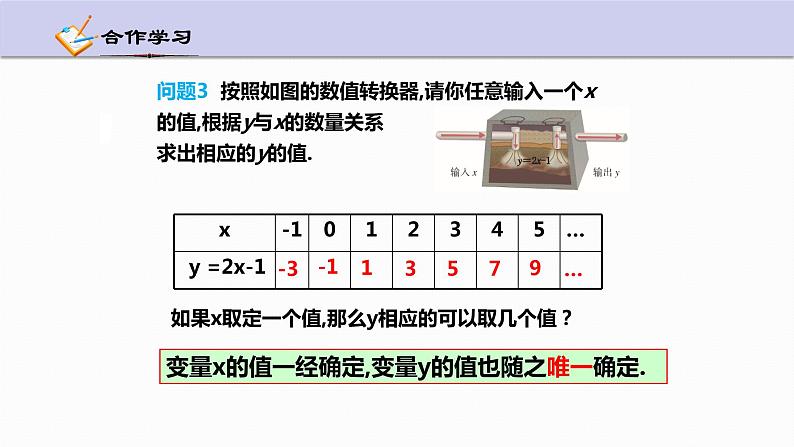
问题3 按照如图的数值转换器,请你任意输入一个x的值,根据y与x的数量关系求出相应的y的值.
变量x的值一经确定,变量y的值也随之唯一确定.
如果x取定一个值,那么y相应的可以取几个值？
一般地,在某个变化过程中,设有两个变量 x,y,如果对于x的每一个确定的值,y都有唯一确定的值，那么就说y是x的函数.
1.小明的哥哥是一名大学生,他利用暑假去一家公司打工，报酬16元/时计算，设小明的哥哥这个月工作的时间为t时，应得报酬为m元，则m=16t.
2.跳远运动员按一定的起跳姿势,其跳远的距离s(米)与助跑的速度v(米/秒)有关.根据经验，跳远的距离s=0.085v2 (0＜v＜10.5)
这个式子也可以表示函数
表示函数关系的等式，就叫做函数解析式，简称函数式.
用函数解析式来表示函数的方法叫做解析法.
例1 某市民用电费的价格是0.53元/千瓦时.设用电量为x千瓦时，应付电费为y元，
（1）求y关于x的函数解析式.
（2）当x=40时，函数值是多少？它的实际意义是什么？
当x=40时，y=0.53x=0.53×40=21.2（元）
用40千瓦时电需付电费21.2元
（3）若某用户的用电量为65千瓦·时，则该用户应付电费为多少元？
0.53×65=34.45（元）
有时把自变量x的一系列值和函数y对应值列成一个表.这种表示函数关系的方法是列表法.
如下表是一年内某城市月份与相应的平均气温.
当m=5时，函数值为 .
当m=3时，T＝ ；
T＝9.3叫做当自变量m=3时的函数值.
用图象来表示函数关系的方法,是图象法.
解析法、列表法、图象法是图象的三种常见的表示方法
如图，图象表示骑车时热量消耗 W (焦)与身体质量x (千克)之间的关系.
P的坐标为（ 　　 ）
当x=30时，Ｗ＝ ；
Ｗ＝252叫做当自变量x=30时的函数值.
下列图象关系中，y是x的函数吗？
对于x的每一个确定的值,y都有唯一确定的值与之对应，所以y是x的函数.
对于x的每一个确定的值,y有两个值与之对应，所以y不是x的函数.
上图中y是x的函数吗?
1.如图所示图形中的曲线不表示y是关于x的函数的是(　　)
2.下列各情景分别可以用哪一幅图来近似的刻画(1)汽车紧急刹车(速度与时间的关系) （ ）(2)人的身高变化(身高与年龄的关系) （ ） (3)跳高运动员跳跃横杆(高度与时间的关系)( ) (4)一面冉冉上升的红旗(高度与时间的关系)( )
3．一个学习小组利用同一块木板，测量了小车从不同高度下滑的时间，他们得到如下数据：
下列说法错误的是(　　)
A．当h＝50 cm时，t＝1.89 sB．随着h逐渐升高，t逐渐变小C．h每增加10 cm，t减小1.23 sD．随着h逐渐升高，小车的速度逐渐加快
4．根据生物学研究结果，青春期男女生身高增长速度呈现如图所示的规律，由图可以判断，下列说法错误的是(　　)
A．男生在13岁时身高增长速度最快B．女生在10岁以后身高增长速度放慢C．11岁时男女生身高增长速度基本相同D．女生身高增长的速度总比男生慢
5.在国内投寄平信应付邮资如下表：
（1）若有四封信件质量分别为5克、10克、30克和50克，则该分别付邮资多少元？
（2）y是x的函数吗？为什么？
（3）若有信件已付邮资1.60元,能确定该信件质量吗？
6．下图是某地2014年黄瓜的销售价格y(元)随月份x变化的图象，请回答下列问题：(1)这个图形反映了哪两个变量之间的关系？(2)根据图形填表：
(3)当x取1～12之间的任一值时，对应几个y值？反之呢？(4)y可以看作x的函数吗？反之呢？
7．下图是小明放学骑自行车回家的折线图，其中t表示时间，s表示离开学校的路程．请根据图象回答下列问题：(1)这个折线图反映了哪两个变量之间的关系？路程s可以看成时间t的函数吗？(2)求当t＝5分钟时的函数值；(3)当10≤t≤15时，对应的函数值是多少？并说明它的实际意义．(4)学校离小明家多远？小明放学骑自行车回家共用了多少分钟？
在某个变化过程中,设有两个变量 x, y,如果对于 x 的每一个确定的值, , 那么就说 , x叫做 .