2024春九年级数学下册极速提分法第1招旋转问题中作辅助线的技巧作业课件新版沪科版

这是一份2024春九年级数学下册极速提分法第1招旋转问题中作辅助线的技巧作业课件新版沪科版，共18页。

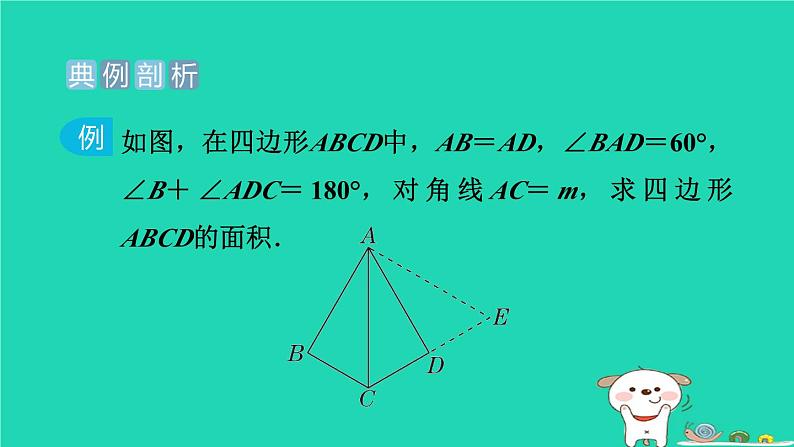
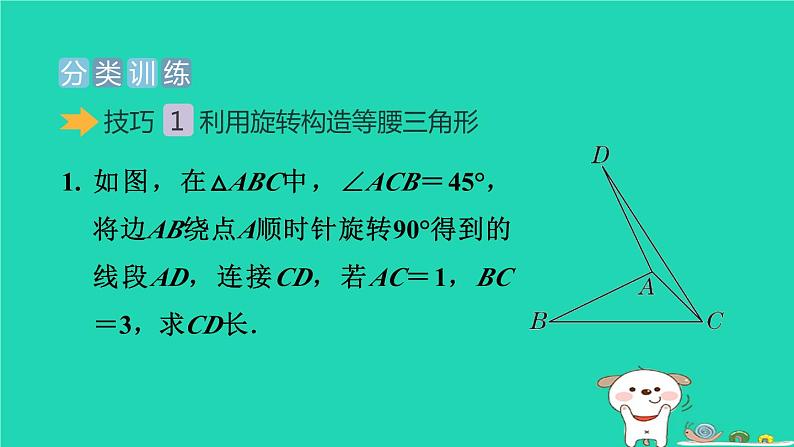
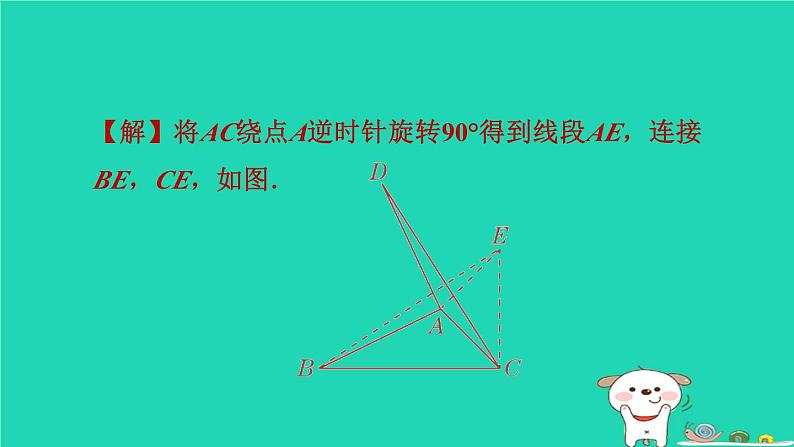
第1招 旋转问题中作辅助线的技巧如图，在四边形ABCD中，AB＝AD，∠BAD＝60°，∠B＋∠ADC＝180°，对角线AC＝m，求四边形ABCD的面积．解题秘方：此四边形不是特殊的四边形，要求面积通常需要将图形转化成规则的图形求解．解：将△ABC绕点A逆时针旋转60°得到△ADE，如图．则AC＝AE，∠B＝∠ADE，∠BAC＝∠DAE.∵∠B＋∠ADC＝180°，∴∠ADE＋∠ADC＝180°.∴点C，D，E在同一条直线上．1. 如图，在△ABC中，∠ACB＝45°，将边AB绕点A顺时针旋转90°得到的线段AD，连接CD，若AC＝1，BC＝3，求CD长．【解】将AC绕点A逆时针旋转90°得到线段AE，连接BE，CE，如图．2. 【问题提出】如图①，四边形ABCD中，AD＝CD，∠ABC＝120°，∠ADC＝60°，AB＝2，BC＝1，求四边形ABCD的面积．【尝试解决】旋转是一种重要的图形变换，当图形中有一组邻边相等时，往往可以通过旋转解决问题．(1)如图②，连接BD，由于AD＝CD，∠ADC＝60°，因此可将△DCB绕点D顺时针旋转60°，得到△DAB′，则△BDB′的形状是__________；等边三角形【点拨】由旋转的性质可得BD＝B′D，旋转角∠BDB′＝60°，∠DAB′＝∠C.又∵∠ABC＋∠ADC＝180°，∴∠BAD＋∠C＝180°.∴∠BAD＋∠DAB′＝180°，即点B，A，B′三点共线．∴△BDB′是等边三角形．(2)在(1)的基础上，求四边形ABCD的面积；3. (1)如图①，在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，且∠EAF＝60°，探究图中线段BE，EF，FD之间的数量关系，小明同学的方法是将△ABE绕点A逆时针旋转120°到△ADG的位置，然后证明△AFE≌△AFG，从而得出结论：____________________.EF＝BE＋FD【解】结论EF＝BE＋FD仍然成立．理由：延长FD到点G，使DG＝BE，连接AG.∵∠B＋∠ADC＝180°，∠ADC＋∠ADG＝180°，∴∠B＝∠ADG.又∵AB＝AD，BE＝DG，∴△ABE≌△ADG(SAS)．∴AE＝AG，∠BAE＝∠DAG.