




- 专题59 二次函数背景下的等腰三角形、直角三角形存在性问题(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用) 试卷 1 次下载
- 专题60 二次函数背景下的特殊平行四边形存在性问题(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用) 试卷 1 次下载
- 专题62 二次函数与圆综合性问题(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用) 试卷 1 次下载
- 专题63 二次函数背景下的倍、半角角度问题(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用) 试卷 1 次下载
- 专题64 反比例函数k的八种几何模型及解法(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用) 试卷 1 次下载
专题61 二次函数背景下的相似三角形问题(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用)
展开在坐标系中确定点,使得由该点及其他点构成的三角形与其他三角形相似,即为“相似三角形存在性问题”.
【相似判定】
判定1:三边对应成比例的两个三角形是相似三角形;
判定2:两边对应成比例且夹角相等的两个三角形是相似三角形;
判定3:有两组角对应相等的三角形是相似三角形.
以上也是坐标系中相似三角形存在性问题的方法来源,根据题目给的已知条件选择恰当的判定方法,解决问题.
【题型分析】
通常相似的两三角形有一个是已知的,而另一三角形中有1或2个动点,即可分为“单动点”类、“双动点”两类问题.
【思路总结】
根据相似三角形的做题经验,可以发现,判定1基本是不会用的,这里也一样不怎么用,对比判定2、3可以发现,都有角相等!
所以,要证相似的两个三角形必然有相等角,关键点也是先找到一组相等角.
然后再找:
思路1:两相等角的两边对应成比例;
思路2:还存在另一组角相等.
事实上,坐标系中在已知点的情况下,线段长度比角的大小更容易表示,因此选择方法可优先考虑思路1.
一、如何得到相等角?
二、如何构造两边成比例或者得到第二组角?
搞定这两个问题就可以了.
例题精讲
【例1】.如图,抛物线y=﹣x2+x+2交x轴于点A,B,交y轴于点C,点M是第一象限内抛物线上一点,过点M作MN⊥x轴于点N.若△MON与△BOC相似,求点M的横坐标.
解:∵抛物线y=﹣x2+x+2交x轴于点A,B,交y轴于点C,
∴当y=0时,0=﹣x2+x+2,
解得x1=﹣1,x2=4,
∴OB=4,
当x=0时,y=2,
∴OC=2,
∵点M是第一象限内抛物线上一点,
∴设M(m,﹣m2+m+2),
∵MN⊥x轴,
∴ON=m,MN=﹣m2+m+2,∠ONM=90°,
∵∠BOC=90°,
∴∠BOC=∠ONM,
∵△MON与△BOC相似,
∴或,
∴=或=,
∴m=或m=﹣1+(负值舍去),
∴点M的横坐标为或﹣1+.
变式训练
【变1-1】.如图,在平面直角坐标系内,已知直线y=x+4与x轴、y轴分别相交于点A和点C,抛物线y=x2+kx+k﹣1图象过点A和点C,抛物线与x轴的另一交点是B,
(1)求出此抛物线的解析式、对称轴以及B点坐标;
(2)若在y轴负半轴上存在点D,能使得以A、C、D为顶点的三角形与△ABC相似,请求出点D的坐标.
解:(1)由x=0得y=0+4=4,则点C的坐标为(0,4);
由y=0得x+4=0,解得x=﹣4,则点A的坐标为(﹣4,0);
把点C(0,4)代入y=x2+kx+k﹣1,得k﹣1=4,
解得:k=5,
∴此抛物线的解析式为y=x2+5x+4,
∴此抛物线的对称轴为x=﹣=﹣.
令y=0得x2+5x+4=0,
解得:x1=﹣1,x2=﹣4,
∴点B的坐标为(﹣1,0).
(2)∵A(﹣4,0),C(0,4),
∴OA=OC=4,
∴∠OCA=∠OAC.
∵∠AOC=90°,OB=1,OC=OA=4,
∴AC==4,AB=OA﹣OB=4﹣1=3.
∵点D在y轴负半轴上,∴∠ADC<∠AOC,即∠ADC<90°.
又∵∠ABC>∠BOC,即∠ABC>90°,∴∠ABC>∠ADC.
∴由条件“以A、C、D为顶点的三角形与△ABC相似”可得△CAD∽△ABC,
∴=,即=,
解得:CD=,
∴OD=CD﹣CO=﹣4=,
∴点D的坐标为(0,﹣).
【例2】.如图,抛物线y=x2+bx+c与x轴交于A(1,0),B两点,与y轴交于点C(0,3).
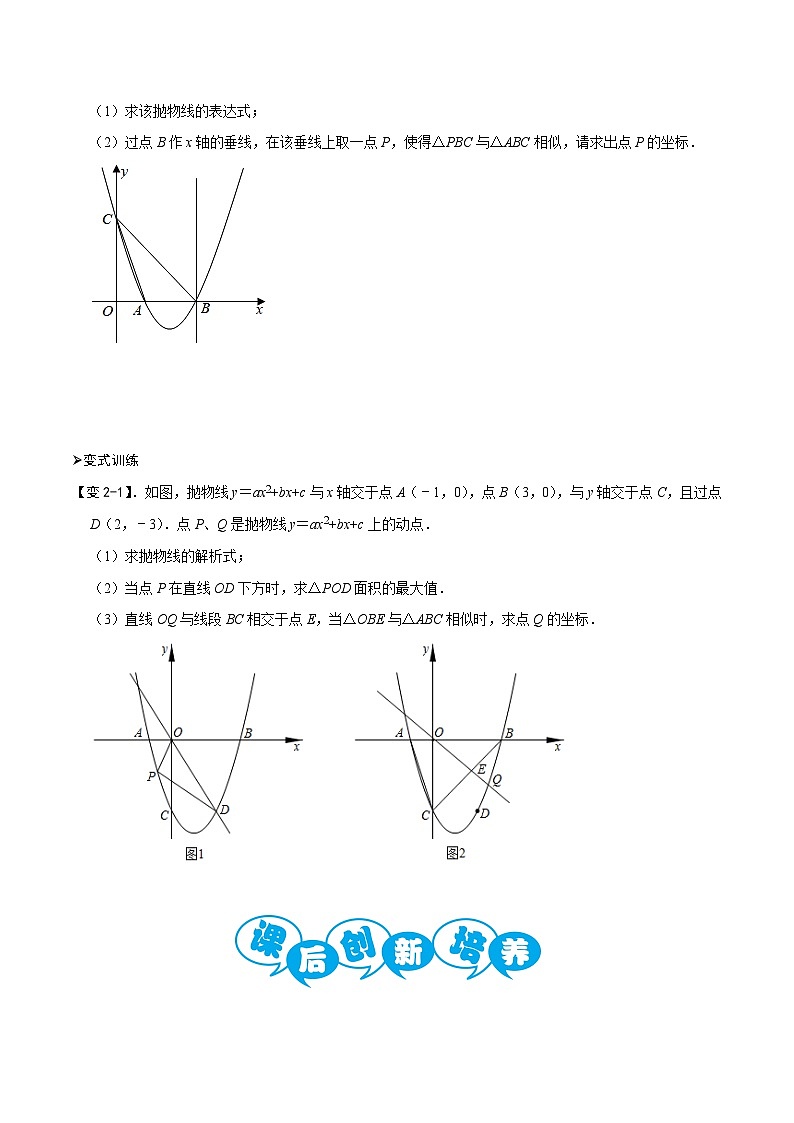
(1)求该抛物线的表达式;
(2)过点B作x轴的垂线,在该垂线上取一点P,使得△PBC与△ABC相似,请求出点P的坐标.
解:(1)把C(0,3)代入y=x2+bx+c,
得c=3,
∴y=x2+bx+3,
把A(1,0)代入y=x2+bx+3,
得1+b+3=0,
解得b=﹣4,
∴该抛物线的表达式为y=x2﹣4x+3.
(2)当点P在点B上方时,如图1,PB=AB,
∵PB⊥x轴,
∴∠ABP=90°,
抛物线y=x2﹣4x+3,当y=0时,则x2﹣4x+3=0,
解得x1=1,x2=3,
∴B(3,0),
∴OB=OC=3,PB=AB=3﹣1=2,
∵∠BOC=90°,
∴∠OBC=∠OCB=45°,
∴∠PBC=∠ABC=45°,
∵==1,
∴△PBC∽△ABC,
此时点P的坐标为(3,2);
如图2,△PBC∽△CBA,且∠CBP=∠ABC=45°,∠BCP=∠BAC,
∴=,
∵BC2=OB2+OC2=32+32=18,BA=2,
∴BP===9,
此时点P的坐标为(3,9);
当点P在点B下方时,∠PBC=135°,∠BAC=∠AOC+∠ACO=90°+∠ACO<135°,
此时△PBC与△ABC不相似,
综上所述,点P的坐标为(3,2)或(3,9).
变式训练
【变2-1】.如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),点B(3,0),与y轴交于点C,且过点D(2,﹣3).点P、Q是抛物线y=ax2+bx+c上的动点.
(1)求抛物线的解析式;
(2)当点P在直线OD下方时,求△POD面积的最大值.
(3)直线OQ与线段BC相交于点E,当△OBE与△ABC相似时,求点Q的坐标.
解:(1)函数的表达式为:y=a(x+1)(x﹣3),将点D坐标代入上式并解得:a=1,
故抛物线的表达式为:y=x2﹣2x﹣3…①;
(2)设点P(m,m2﹣2m﹣3),
①当点P在第三象限时,
设直线PD与y轴交于点G,设点P(m,m2﹣2m﹣3),
将点P、D的坐标代入一次函数表达式:y=sx+t并解得:
直线PD的表达式为:y=mx﹣3﹣2m,则OG=3+2m,
S△POD=×OG(xD﹣xP)=(3+2m)(2﹣m)=﹣m2+m+3,
②当点P在第四象限时,
设PD交y轴于点M,
同理可得:S△POD=×OM(xD﹣xP)=﹣m2+m+3,
综上,S△POD=﹣m2+m+3,
∵﹣1<0,故S△POD有最大值,当m=时,其最大值为;
(3)∵OB=OC=3,
∴∠OCB=∠OBC=45°,
∵∠ABC=∠OBE,故△OBE与△ABC相似时,分为两种情况:
①当∠ACB=∠BOQ时,
AB=4,BC=3,AC=,
过点A作AH⊥BC于点H,
S△ABC=×AH×BC=AB×OC,解得:AH=2,
则sin∠ACB==,则tan∠ACB=2,
则直线OQ的表达式为:y=﹣2x…②,
联立①②并解得:x=或﹣,
故点Q(,﹣2)或(﹣,2),
②∠BAC=∠BOQ时,
tan∠BAC==3=tan∠BOQ,
则点Q(n,﹣3n),
则直线OQ的表达式为:y=﹣3x…③,
联立①③并解得:x=,
故点Q(,)或(,);
综上,当△OBE与△ABC相似时,Q的坐标为:(,﹣2)或(﹣,2)或(,)或(,).
1.抛物线y=﹣x2平移后的位置如图所示,点A,B坐标分别为(﹣1,0)、(3,0),设平移后的抛物线与y轴交于点C,其顶点为D.
(1)求平移后的抛物线的解析式和点D的坐标;
(2)∠ACB和∠ABD是否相等?请证明你的结论;
(3)点P在平移后的抛物线的对称轴上,且△CDP与△ABC相似,求点P的坐标.
解:(1)∵将抛物线y=﹣x2平移,平移后的抛物线与x轴交于点A(﹣1,0)和点B(3,0),
∴平移后的抛物线的表达式为y=﹣(x+1)(x﹣3)=﹣x2+2x+3,即y=﹣x2+2x+3,
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点D的坐标为(1,4);
(2)∠ACB与∠ABD相等,理由如下:
如图,∵y=﹣x2+2x+3,
∴点x=0时,y=3,即C点坐标为(0,3),
又∵B(3,0),∠BOC=90°,
∴OB=OC,∠OBC=∠OCB=45°.
在△BCD中,∵BC2=32+32=18,CD2=12+12=2,BD2=22+42=20,
∴BC2+CD2=BD2,
∴∠BCD=90°,
∴tan∠CBD===,
∵在△AOC中,∠AOC=90°,
∴tan∠ACO==,
∴tan∠ACO=tan∠CBD,
∴∠ACO=∠CBD,
∴∠ACO+∠OCB=∠CBD+∠OBC,
即∠ACB=∠ABD;
(3)∵点P在平移后的抛物线的对称轴上,而y=﹣x2+2x+3的对称轴为x=1,
∴可设P点的坐标为(1,n).
∵△ABC是锐角三角形,
∴当△CDP与△ABC相似时,△CDP也是锐角三角形,
∴n<4,即点P只能在点D的下方,
又∵∠CDP=∠ABC=45°,
∴D与B是对应点,分两种情况:
①如果△CDP∽△ABC,那么=,
即=,
解得n=,
∴P点的坐标为(1,);
②如果△CDP∽△CBA,那么=,
即=,
解得n=,
∴P点的坐标为(1,).
综上可知P点的坐标为(1,)或(1,).
2.如图,已知△ABC中,∠ACB=90°,以AB所在直线为x轴,过c点的直线为y轴建立平面直角坐标系.此时,A点坐标为(﹣1,0),B点坐标为(4,0)
(1)试求点C的坐标;
(2)若抛物线y=ax2+bx+c过△ABC的三个顶点,求抛物线的解析式;
(3)点D(1,m)在抛物线上,过点A的直线y=﹣x﹣1交(2)中的抛物线于点E,那么在x轴上点B的左侧是否存在点P,使以P、B、D为顶点的三角形与△ABE相似?若存在,求出P点坐标;若不存在,说明理由.
解:(1)在Rt△ABC中,∠ACB=90°,OC⊥AB,
由射影定理,得:OC2=OA•OB=4,即OC=2,
∴C(0,2);
(2)∵抛物线经过A(﹣1,0),B(4,0),C(0,2),
可设抛物线的解析式为y=a(x+1)(x﹣4)(a≠0),则有:
2=a(0+1)(0﹣4),a=﹣,
∴y=﹣(x+1)(x﹣4)=﹣x2+x+2;
(3)存在符合条件的P点,且P(,0)或(﹣,0).
根据抛物线的解析式易知:D(1,3),
联立直线AE和抛物线的解析式有:
,
解得,,
∴E(6,﹣7),
∴tan∠DBO==1,即∠DBO=45°,tan∠EAB==1,即∠EAB=45°,
∴∠DBA=∠EAB,
若以P、B、D为顶点的三角形与△ABE相似,则有两种情况:
①△PBD∽△BAE;②△PBD∽△EAB.
易知BD=3,EA=7,AB=5,
由①得:,即,即PB=,OP=OB﹣PB=,
由②得:,即,即P′B=,OP′=OB﹣BP′=﹣,
∴P(,0)或(﹣,0).
3.如图已知直线y=x+与抛物线y=ax2+bx+c相交于A(﹣1,0),B(4,m)两点,抛物线y=ax2+bx+c交y轴于点C(0,﹣),交x轴正半轴于D点,抛物线的顶点为M.
(1)求抛物线的解析式;
(2)设点P为直线AB下方的抛物线上一动点,当△PAB的面积最大时,求△PAB的面积及点P的坐标;
(3)若点Q为x轴上一动点,点N在抛物线上且位于其对称轴右侧,当△QMN与△MAD相似时,求N点的坐标.
解:(1)将点B(4,m)代入y=x+,
∴m=,
将点A(﹣1,0),B(4,),C(0,﹣)代入y=ax2+bx+c,
解得a=,b=﹣1,c=﹣,
∴函数解析式为y=x2﹣x﹣;
(2)设P(n,n2﹣n﹣),
则经过点P且与直线y=x+垂直的直线解析式为y=﹣2x+n2+n﹣,
直线y=x+与其垂线的交点G(n2+n﹣,n2+n+),
∴GP=(﹣n2+3n+4),
当n=时,GP最大,此时△PAB的面积最大,
∴P(,﹣),
∵AB=,PG=,
∴△PAB的面积=××=;
(3)∵M(1,﹣2),A(﹣1,0),D(3,0),
∴AM=2,AD=4,MD=2,
∴△MAD是等腰直角三角形,
∵△QMN与△MAD相似,
∴△QMN是等腰直角三角形,
设N(t,t2﹣t﹣)
①如图1,当MQ⊥QN时,N(3,0);
②如图2,当QN⊥MN时,过点N作NR⊥x轴,过点M作MS⊥RN交于点S,
∵QN=MN,∠QNM=90°,
∴△MNS≌△NMS(AAS)
∴t﹣1=﹣t2+t+,
∴t=±,
∴t>1,
∴t=,
∴N(,1﹣);
③如图3,当QN⊥MQ时,过点Q作x轴的垂线,过点N作NS∥x轴,过点M作MR∥x轴,与过Q点的垂线分别交于点S、R;
∵QN=MQ,∠MQN=90°,
∴△MQR≌△QNS(AAS),
∴SQ=QR=2,
∴t+2=1+t2﹣t﹣,
∴t=5,
∴N(5,6);
④如图4,当MN⊥NQ时,过点M作MR⊥x轴,过点Q作QS⊥x轴,
过点N作x轴的平行线,与两垂线交于点R、S;
∵QN=MN,∠MNQ=90°,
∴△MNR≌△NQS(AAS),
∴SQ=RN,
∴t2﹣t﹣=t﹣1,
∴t=2±,
∵t>1,
∴t=2+,
∴N(2+,1+);
综上所述:N(3,0)或N(2+,1+)或N(5,6)或N(,1﹣).
4.如图,已知抛物线经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
(1)直接写出:b= 2 ,c= 1 ;
(2)过点P且与y轴平行的直线l与直线AB,AC分别交于点E,F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C,P,Q为顶点的三角形与△ABC相似,若存在,直接写出点Q的坐标,若不存在,请说明理由.
解:(1)将点 A(0,1),B(﹣9,10)代入,
∴,
解得 ,
∴抛物线的解析式为 ,
∴b=2,c=1,
故答案为:2,1;
(2)∵AC∥x 轴,A(0,1),
∴,
∴x1=﹣6,x2=0,
∴C (﹣6,1),
∵A(0,1),B(﹣9,10),
∴直线 AB 的解析式为 y=﹣x+1,
设点 ,则 E(m,﹣m+1),
∴,
∵AC⊥EP,AC=6,
∴S四边形AECP=S△AEC+S△APC
=×AC×EF+
=×AC×(EF+PF)
=×AC×PE
=×6×(﹣m2﹣3m)
=﹣m2﹣9m
=﹣(m+)2+,
∵﹣6<m<0,
当 时,四边形 AECP 的面积的最大值是 ,
此时点 ;
(3)存在点Q,使得以C,P,Q为顶点的三角形与△ABC相似,理由如下:
∵,
∴P(﹣3,﹣2),
∴PF=yF﹣yP=3,CF=xF﹣xC=3,
∴PF=CF,
∴∠PCF=45°.
同理可得:∠EAF=45°,
∴∠PCF=∠EAF,
∴在直线 AC 上存在满足条件的 Q,
设 Q(t,1),
∵A(0,1),B(﹣9,10),C (﹣6,1),
∴,AC=6,,
以 C,P,Q 为顶点的三角形与△ABC相似,
①当△CPQ∽△ABC时,
∴,
∴,
∴t=﹣4,
∴Q(﹣4,1);
②当△CQP∽△ABC时,
∴,
∴,
∴t=3,
∴Q(3,1);
综上所述:Q点坐标为(﹣4,1)或(3,1).
5.已知抛物线经过点A(﹣2,0),B(0,﹣4),与x轴交于另一点C,连接BC.
(1)求抛物线的解析式;
(2)如图,P是第一象限内抛物线上一点,且S△PBO=S△PBC,求直线AP的表达式;
(3)在抛物线上是否存在点D,直线BD交x轴于点E,使△ABE与以A,B,C,E中的三点为顶点的三角形相似(不重合)?若存在,请直接写出点D的坐标;若不存在,请说明理由.
解:(1)把点A(﹣2,0),B(0、﹣4)代入抛物线y=x2+bx+c中得:
,解得:,
∴抛物线的解析式为:y=x2﹣x﹣4;
(2)当y=0时,x2﹣x﹣4=0,
解得:x=﹣2或4,
∴C(4,0),
如图1,过O作OE⊥BP于E,过C作CF⊥BP于F,设PB交x轴于G,
∵S△PBO=S△PBC,
∴,
∴OE=CF,
易得△OEG≌△CFG,
∴OG=CG=2,
设P(x,x2﹣x﹣4),过P作PM⊥y轴于M,
tan∠PBM===,
∴BM=2PM,
∴4+x2﹣x﹣4=2x,
x2﹣6x=0,
x1=0(舍),x2=6,
∴P(6,8),
∴AP的解析式为:y=x+2,
BC的解析式为:y=x﹣4,
∴AP∥BC;
(3)以A,B,C,E中的三点为顶点的三角形有△ABC、△ABE、△ACE、△BCE,四种,其中△ABE重合,不符合条件,△ACE不能构成三角形,
∴当△ABE与以A,B,C,E中的三点为顶点的三角形相似,存在两个三角形:△ABC和△BCE,
①当△ABE与以A,B,C中的三点为顶点的三角形相似,如图2,
∵∠BAE=∠BAC,∠ABE≠∠ABC,
∴∠ABE=∠ACB=45°,
∴△ABE∽△ACB,
∴,
∴,
∴AE=,OE=﹣2=
∴E(,0),
∵B(0,﹣4),
∴BE:y=3x﹣4,
则x2﹣x﹣4=3x﹣4,
x1=0(舍),x2=8,
∴D(8,20);
②当△ABE与以B,C、E中的三点为顶点的三角形相似,如图3,此时E在C的左边,
∵∠BEA=∠BEC,
∴当∠ABE=∠BCE时,△ABE∽△BCE,
∴==,
设BE=2m,CE=4m,
Rt△BOE中,由勾股定理得:BE2=OE2+OB2,
∴,
3m2﹣8m+8=0,
(m﹣2)(3m﹣2)=0,
m1=2,m2=,
∴OE=4m﹣4=12或,
∵OE=<2,∠AEB或∠BEC是钝角,此时△ABE与以B,C、E中的三点为顶点的三角形不相似,如图4,
∴E(﹣12,0);
同理得BE的解析式为:y=﹣x﹣4,
﹣x﹣4=x2﹣x﹣4,
x=或0(舍)
∴D(,﹣);
同理可得E在C的右边时,△ABE∽△BCE,
∴=,
设AE=2m,BE=4m,
Rt△BOE中,由勾股定理得:BE2=OE2+OB2,
∴,
3m2+2m﹣5=0,
(m+)(3m﹣)=0,
m1=﹣,m2=,
∴OE=﹣12(舍)或,
∵OE=<4,∠BEC是钝角,此时△ABE与以B,C、E中的三点为顶点的三角形不相似,
综上,点D的坐标为(8,20)或(,﹣
6.如图,已知抛物线y=ax2+bx+6经过两点A(﹣1,0),B(3,0),C是抛物线与y轴的交点.
(1)求抛物线的解析式;
(2)点P(m,n)在平面直角坐标系第一象限内的抛物线上运动,直线CP与x轴交于点Q,当∠BQC=∠BCO时,求此时P点坐标;
(3)点M在抛物线上运动,点N在y轴上运动,是否存在点M、点N使得∠CNM=90°,且△CMN与△OBC相似,如果存在,请求出点M和点N的坐标.
解:(1)把A(﹣1,0),B(3,0)代入y=ax2+bx+6得:
,解得,
∴抛物线的解析式为y=﹣2x2+4x+6;
(2)由y=﹣2x2+4x+6得C(0,6),
∴OC=6,
当Q在x轴正半轴,如图:
∵∠BQC=∠BCO,且∠COB=∠QOC,
∴△COB∽△QOC,
∴=,即=,
∴OQ=12,
∴Q(12,0),
设直线CQ解析式为y=kx+6,
则0=12k+6,
∴k=﹣,即直线CQ为y=﹣x+6,
由得(与C重合,舍去)或,
∴P(,),
当Q在x轴负半轴,如图:
同理可得:△BOC∽△BCQ,
∴=,即BC2=OB•BQ,
而OC=6,OB=3,
∴BC=3,
∴(3)2=3×BQ,
∴BQ=15,
∴Q(﹣12,0),
设直线CQ为y=mx+6,则0=﹣12m+6,
解得m=,
∴直线CQ为y=x+6,
由得(舍去)或,
∴P(,),
综上所述,P点坐标为(,)或(,),
(3)设M(t,﹣2t2+4t+6),则N(0,﹣2t2+4t+6),
∴MN=|t|,CN=|2t2﹣4t|,
∵OC=6,OB=3,
∴OC=2OB,
∵△CMN与△OBC相似,
∴MN=2CN或CN=2MN,
①MN=2CN时,如图:
∴|t|=2|2t2﹣4t|,
解得t=或t=或t=0(舍去),
∴M(,),N(0,)或M(,),N(0,);
②CN=2MN时,如图:
∴|2t2﹣4t|=2|t|,
解得t=0(舍去)或t=3(M与B重合,舍去)或t=1,
∴M(1,8),N(0,8),
综上所述,M(,),N(0,)或M(,),N(0,)或M(1,8),N(0,8).
7.如图,抛物线与x轴交于A,B两点,点A,B分别位于原点的左、右两侧,BO=3AO=3,过点B的直线与y轴正半轴和抛物线的交点分别为点C,D,.
(1)求b,c的值;
(2)求直线CD的函数解析式;
(3)求∠ADB的度数;
(4)点P在抛物线的对称轴上且在x轴下方,点Q在射线BA上,当△ABD与△BPQ相似时,请直接写出所有满足条件的点Q的坐标.
解:(1)∵点A,B分别位于原点的左、右两侧,BO=3AO=3,
∴A(﹣1,0),B(3,0),
把A(﹣1,0),B(3,0)代入y=x2+bx+c,
得,
解得:,
∴b=﹣,c=﹣;
(2)如图1,过点D作DE⊥AB于E,
则∠DEB=∠COB=90°,
∴DE∥OC,
∴=,
∵BC=CD,OB=3,
∴=,
∴OE=,
∴点D横坐标为﹣,
当x=﹣时,y=×(﹣)2﹣×(﹣)﹣=+1,
∴点D坐标为(﹣,+1),
设直线BD的函数解析式为y=kx+n,把B(3,0),D(﹣,+1)代入,
得,
解得:,
∴直线BD的函数解析式为y=﹣x+;
(3)如图2,连接AC,
∵直线BD的函数解析式为y=﹣x+,
∴C(0,),
∵A(﹣1,0),D(﹣,+1),
∴AC2=OA2+OC2=12+()2=4,则AC=2,
BC2=OB2+OC2=32+()2=12,则BC=2,
∴AB=3﹣(﹣1)=4,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴∠ACD=180°﹣90°=90°,
∵BC=CD,
∴CD=2,
∴tan∠ADB===1,
∴∠ADB=45°;
(4)在△ABD中,tan∠ABD==,
∴∠ABD=30°,
∵∠ADB=45°,
∴∠BAD=180°﹣(∠ABD+∠ADB)=180°﹣(30°+45°)=105°,
∵CD=2,BC=CD=2,
∴BD=BC+CD=2+2,
由(3)知:AC=CD=2,∠ACD=90°,AB=4,
∴AD=2,
∵y=x2﹣x﹣,
∴对称轴为直线x=1.
∵点P在抛物线的对称轴上且在x轴下方,点Q在射线BA上,
∴∠PBQ<90°,
∴分两种情况:
①当∠PBQ=∠ABD=30°时,如图3,设对称轴与x轴交于点M,
则M(1,0),
∴BM=3﹣1=2,
∴PM=BM•tan∠PBQ=2×tan30°=,
∵点P在抛物线的对称轴上且在x轴下方,
∴P(1,﹣),
BP===,
∵△ABD与△BPQ相似,且∠PBQ=∠ABD,
∴=或=,
∴=或=,
∴BQ=或BQ=,
∴Q(,0)或(,0);
②当∠PBQ=∠ADB=45°时,如图4,
∵PM=BM•tan∠PBQ=2tan45°=2,
∴P(1,﹣2),
∴BP=2,
∵△ABD与△BPQ相似,且∠PBQ=∠ADB,
∴=或=,
∴=或=,
∴BQ=2﹣2或2+2,
∴Q(5﹣2,0)或(1﹣2,0);
综上所述,点Q的坐标为Q(,0)或Q(,0)或Q(5﹣2,0)或Q(1﹣2,0).
8.在平面直角坐标系xOy中,已知抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C(0,﹣2).
(1)求抛物线的函数表达式;
(2)如图1,点D为第四象限抛物线上一点,连接AD,BC交于点E,求的最大值;
(3)如图2,连接AC,BC,过点O作直线l∥BC,点P,Q分别为直线l和抛物线上的点,试探究:在第一象限是否存在这样的点P,Q,使△PQB∽△CAB?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
解:(1)设抛物线的解析式为y=a(x+1)(x﹣4).
将C(0,﹣2)代入得:﹣4a=﹣2,
解得a=,
∴抛物线的解析式为y=(x+1)(x﹣4),即y=x2﹣x﹣2.
(2)过点D作DG⊥x轴于点G,交BC于点F,过点A作AK⊥x轴交BC的延长线于点K,
∴AK∥DG,
∴△AKE∽△DFE,
∴=.
设直线BC的解析式为y=kx+b1,
∴,
解得,
∴直线BC的解析式为y=x﹣2,
∵A(﹣1,0),
∴y=﹣﹣2=﹣,
∴AK=,
设D(m,m2﹣m﹣2),则F(m,m﹣2),
∴DF=m﹣2﹣m2+m+2=﹣m2+2m.
∴==﹣(m﹣2)2+.
∴当m=2时,有最大值,最大值是.
(3)符合条件的点P的坐标为(,)或(,).
∵l∥BC,
∴直线l的解析式为y=x,
设P(a1,),
①当点P在直线BQ右侧时,如图2,过点P作PN⊥x轴于点N,过点Q作QM⊥直线PN于点M,
∵A(﹣1,0),C(0,﹣2),B(4,0),
∴AC=,AB=5,BC=2,
∵AC2+BC2=AB2,
∴∠ACB=90°,
∵△PQB∽△CAB,
∴==,
∵∠QMP=∠BNP=90°,
∴∠MQP+∠MPQ=90°,∠MPQ+∠BPN=90°,
∴∠MQP=∠BPN,
∴△QPM∽△PBN,
∴===,
∴QM=,PM=(a1﹣4)=a1﹣2,
∴MN=a1﹣2,ON﹣QM=a1﹣=a1,
∴Q(a1,a1﹣2),
将点Q的坐标代入抛物线的解析式得×(a1)2﹣×a1﹣2=a1﹣2,
解得a1=0(舍去)或a1=.
∴P(,).
②当点P在直线BQ左侧时,
由①的方法同理可得点Q的坐标为(a1,2).
此时点P的坐标为(,).
综上所述,符合条件的点P的坐标是(,)或(,).
9.如图,直线y=﹣x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣x2+bx+c经过点A,B.
(1)求点B的坐标和抛物线的解析式;
(2)M为线段OA上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.若以B,P,N为顶点的三角形与△APM相似,求点M的坐标;
(3)将抛物线在0≤x≤3之间的部分记为图象L,将图象L在直线y=t上方部分沿直线y=t翻折,其余部分保持不动,得到一个新的函数图象,记这个函数的最大值为a,最小值为b,若a﹣b≤3,请直接写出t的取值范围.
解:(1)将(3,0)代入y=﹣x+c得0=﹣2+c,
解得c=2,
∴y=﹣x+2.
将x=0代入y=﹣x+2得y=2,
∴点B坐标为(0,2).
将(3,0),(0,2)代入y=﹣x2+bx+c得,
解得,
∴y=﹣x2+x+2.
(2)如图,当BM∥AM时满足题意,
点B,N关于抛物线对称轴对称,
∵y=﹣x2+x+2,
∴抛物线对称轴为直线x=﹣=,
∴点N坐标为(,2),
∴点M坐标为(,0).
如图,当∠NBP=90°时符合题意,
作NC⊥y轴于点C,则N(m,﹣m2+m+2),
∵∠NBC+∠ABO=∠ABO+∠BAO=90°,
∴∠NBC=∠BAO,
∴△BCN∽△AOB,
∴=,即,
解得m=,
∴点M坐标为(,0).
综上所述,点M坐标为(,0)或(,0).
(3)∵y=﹣x2+x+2=﹣(x﹣)2+,
∴抛物线顶点坐标为(,),
∴翻折后顶点坐标为(,2t﹣),
当点A为最低点时,t﹣0≤3,
解得t≤3,
令t﹣(2t﹣)=3,
解得t=,
∴≤t≤3.
10.如图所示,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与x轴交于A、B两点(点A在点B的左侧),与y轴相交于点C,B、C两点的坐标分别为(1,0)、(0,﹣3),直线y=kx+3k经过点A,与y轴交于点D.
(1)求抛物线的函数表达式;
(2)点E是抛物线上一动点(不与点C重合),连接AE,过点E作EF⊥x轴,垂足为F,若△AEF是等腰直角三角形,求点E的坐标;
(3)在(2)的条件下,若在直线y=kx+3k上存在一点G使得△DFG与△AOC相似,求出k的值.
解:(1)∵直线y=kx+3k经过点A,则点A的坐标为(﹣3,0),
将点A、B、C的坐标代入抛物线表达式得:,解得,
故抛物线的表达式为y=x2+2x﹣3;
(2)设点E的坐标为(x,x2+2x﹣3),则AF=|x+3|,EF=|x2+2x﹣3|,
∵△AEF是等腰直角三角形,
∴AF=EF,
∴|x2+2x﹣3|=|x+3|,
∴x=﹣3(舍去)或x=0(舍去)或x=2,
故点E的坐标为(2,5);
(3)∵CO=BO=3,故△AOC为等腰直角三角形,
当△DFG与△AOC相似时,则△DFG为等腰直角三角形,
显然∠DFG不可能为直角,
∵直线y=kx+3k与y轴交于点D,则点D(0,3k),
由(2)知,点F(2,0),
①当∠FDG为直角时,
∵点G在直线AD上,故在∠FDG的前提下,总能找到GD=DF,
故只需要DF⊥AD即可,
在等腰Rt△FDG中,
由直线AD的表达式为:y=kx+3k,则tan∠DOA=k,
而tan∠DFO====,
解得k=±;
②当∠FGD为直角时,如下图,
过点G作MN∥y轴,交x轴于点N,交过点D与x轴的平行线于点M,则DG=GF,
设点G的坐标为(t,kt+3k),
则MD=﹣t,MG=3k﹣tk﹣3k=﹣kt;GN=kt+3k,FN=2﹣t,
∵∠MGD+∠FGN=90°,∠FGN+∠GFN=90°,
∴∠MGD=∠GFN,
∵∠GMD=∠FNG=90°,GD=FG,
∴△GMD≌△FNG(AAS),
∴MD=GN,MG=NF,
即﹣t=kt+3k且﹣kt=2﹣t,
解得k=2或﹣;
当∠DFG=90°时,过点G作GH⊥x轴于H,则△ODF≌△HFG,
∴GH=OF=2,HF=OD=3k,
∵y=﹣2时,﹣2=kx+3k,
∴x=,
∴2+=3k,
解得k=2或﹣
综上,k=±或2或﹣.
11.如图,已知A(﹣2,0),B(4,0),抛物线y=ax2+bx﹣1过A、B两点,并与过A点的直线y=﹣x﹣1交于点C.
(1)求抛物线解析式及对称轴;
(2)在抛物线的对称轴上是否存在一点P,使四边形ACPO的周长最小?若存在,求出点P的坐标,若不存在,请说明理由;
(3)点M为y轴右侧抛物线上一点,过点M作直线AC的垂线,垂足为N.问:是否存在这样的点N,使以点M、N、C为顶点的三角形与△AOC相似,若存在,求出点N的坐标,若不存在,请说明理由.
解:(1)把A(﹣2,0),B(4,0)代入抛物线y=ax2+bx﹣1,得
解得
∴抛物线解析式为:y=
∴抛物线对称轴为直线x=﹣
(2)存在
使四边形ACPO的周长最小,只需PC+PO最小
∴取点C(0,﹣1)关于直线x=1的对称点C′(2,﹣1),连C′O与直线x=1的交点即为P点.
设过点C′、O直线解析式为:y=kx
∴k=﹣
∴y=﹣
则P点坐标为(1,﹣)
(3)当△AOC∽△MNC时,
如图,延长MN交y轴于点D,过点N作NE⊥y轴于点E
∵∠ACO=∠NCD,∠AOC=∠CND=90°
∴∠CDN=∠CAO
由相似,∠CAO=∠CMN
∴∠CDN=∠CMN
∵MN⊥AC
∴M、D关于AN对称,则N为DM中点
设点N坐标为(a,﹣a﹣1)
由△EDN∽△OAC
∴ED=2a
∴点D坐标为(0,﹣)
∵N为DM中点
∴点M坐标为(2a,)
把M代入y=,解得
a=0(舍去)或a=4
∴a=4
则N点坐标为(4,﹣3)
当△AOC∽△CNM时,∠CAO=∠NCM
∴CM∥AB则点C关于直线x=1的对称点C′即为点M
由(2)M为(2,﹣1)
∴由相似CN=,MN=
由面积法求N到MC距离为
则N点坐标为(,﹣)
∴N点坐标为(4,﹣3)或(,﹣)
12.抛物线L:y=﹣x2+bx+c经过点A(0,1),与它的对称轴直线x=1交于点B.
(1)求出抛物线L的解析式;
(2)如图1,过定点的直线y=kx﹣k+4(k<0)与抛物线L交于点M、N.若△BMN的面积等于1,求k的值;
(3)如图2,将抛物线L向上平移m(m>0)个单位长度得到抛物线L1,抛物线L1与y轴交于点C,过点C作y轴的垂线交抛物线L1于另一点D,F为抛物线L1的对称轴与x轴的交点,P为线段OC上一点,若△PCD与△POF相似,并且符合条件的点P恰有2个,求m的值及相应点P的坐标.
解:(1)由题意知,
解得:,
∴抛物线L的解析式为y=﹣x2+2x+1;
(2)如图1,
∵y=kx﹣k+4=k(x﹣1)+4,
∴当x=1时,y=4,即该直线所过定点G坐标为(1,4),
∵y=﹣x2+2x+1=﹣(x﹣1)2+2,
∴点B(1,2),
则BG=2,
∵S△BMN=1,即S△BNG﹣S△BMG=BG•(xN﹣1)﹣BG•(xM﹣1)=1,
∴xN﹣xM=1,
由得x2+(k﹣2)x﹣k+3=0,
解得:x==,
则xN=、xM=,
由xN﹣xM=1得=1,
∴k=±3,
∵k<0,
∴k=﹣3;
(3)如图2,
设抛物线L1的解析式为y=﹣x2+2x+1+m,
∴C(0,1+m)、D(2,1+m)、F(1,0),
设P(0,t),
①当△PCD∽△FOP时,,
∴,
∴t2﹣(1+m)t+2=0①;
②当△PCD∽△POF时,,
∴,
∴t=(m+1)②;
(Ⅰ)当方程①有两个相等实数根时,
Δ=(1+m)2﹣8=0,
解得:m=2﹣1(负值舍去),
此时方程①有两个相等实数根t1=t2=,
方程②有一个实数根t=,
∴m=2﹣1,
此时点P的坐标为(0,)和(0,);
(Ⅱ)当方程①有两个不相等的实数根时,
把②代入①,得:(m+1)2﹣(m+1)2+2=0,
解得:m=2(负值舍去),
此时,方程①有两个不相等的实数根t1=1、t2=2,
方程②有一个实数根t=1,
∴m=2,此时点P的坐标为(0,1)和(0,2);
综上,当m=2﹣1时,点P的坐标为(0,)和(0,);
当m=2时,点P的坐标为(0,1)和(0,2).
13.设抛物线y=ax2+bx﹣2与x轴交于两个不同的点A(﹣1,0)、B(m,0),与y轴交于点C,且∠ACB=90度.
(1)求m的值和抛物线的解析式;
(2)已知点D(1,n)在抛物线上,过点A的直线y=x+1交抛物线于另一点E.若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标;
(3)在(2)的条件下,△BDP的外接圆半径等于 或 .
解:(1)令x=0,得y=﹣2,
∴C(0,﹣2),
∵∠ACB=90°,CO⊥AB,
∴△AOC∽△COB,
∴OA•OB=OC2
∴OB=,
∴m=4,
将A(﹣1,0),B(4,0)代入y=ax2+bx﹣2,
得,
∴抛物线的解析式为y=x2﹣x﹣2.
(2)D(1,n)代入y=x2﹣x﹣2,得n=﹣3,
由,得,,
∴E(6,7),
过E作EH⊥x轴于H,则H(6,0)
∴AH=EH=7
∴∠EAH=45°
过D作DF⊥x轴于F,则F(1,0)
∴BF=DF=3
∴∠DBF=45°
∴∠EAH=∠DBF=45°
∴∠DBH=135°,
90°<∠EBA<135°
则点P只能在点B的左侧,有以下两种情况:
①若△DBP1∽△EAB,则
∴BP1===
∴OP1=4﹣=,
∴P1(,0).
②若△DBP2∽△BAE,则
∴BP2===
∴OP2=﹣4=
∴P2(﹣,0).
综合①、②,得点P的坐标为:P1(,0)或P2(﹣,0).
(3)或.
如图所示:先作△BPD的外接圆,过P作直径PM,连接DM,作DF⊥x轴于F.
∵∠PMD=∠PBD,∠DFP=∠PDM,
∴△PMD和△FBD相似,
∴,
∴PD===,
DF=3,
BD==3,
∴PM==,
∴△BPD的外接圆的半径=;
同理可求出当P点在x轴的负半轴上时,△BPD的外接圆的半径=.
14.如图1,在平面直角坐标系中,抛物线y=x2+x﹣与x轴交于点A、B(点A在点B右侧),点D为抛物线的顶点,点C在y轴的正半轴上,CD交x轴于点F,△CAD绕点C顺时针旋转得到△CFE,点A恰好旋转到点F,连接BE.
(1)求点A、B、D的坐标;
(2)求证:四边形BFCE是平行四边形;
(3)如图2,过顶点D作DD1⊥x轴于点D1,点P是抛物线上一动点,过点P作PM⊥x轴,点M为垂足,使得△PAM与△DD1A相似(不含全等).
①求出一个满足以上条件的点P的横坐标;
②直接回答这样的点P共有几个?
解:(1)令x2+x﹣=0,
解得x1=1,x2=﹣7.
∴A(1,0),B(﹣7,0).
由y=x2+x﹣=(x+3)2﹣2得,D(﹣3,﹣2);
(2)证明:∵DD1⊥x轴于点D1,
∴∠COF=∠DD1F=90°,
∵∠D1FD=∠CFO,
∴△DD1F∽△COF,
∴=,
∵D(﹣3,﹣2),
∴D1D=2,OD1=3,
∵AC=CF,CO⊥AF
∴OF=OA=1
∴D1F=D1O﹣OF=3﹣1=2,
∴=,
∴OC=,
∴CA=CF=FA=2,
∴△ACF是等边三角形,
∴∠AFC=∠ACF,
∵△CAD绕点C顺时针旋转得到△CFE,
∴∠ECF=∠AFC=60°,
∴EC∥BF,
∵EC=DC==6,
∵BF=6,
∴EC=BF,
∴四边形BFCE是平行四边形;
(3)∵点P是抛物线上一动点,
∴设P点(x,x2+x﹣),
①当点P在B点的左侧时,
∵△PAM与△DD1A相似,
∴或=,
∴=或=,
解得:x1=1(不合题意舍去),x2=﹣11或x1=1(不合题意舍去)x2=﹣;
当点P在A点的右侧时,
∵△PAM与△DD1A相似,
∴=或=,
∴=或=,
解得:x1=1(不合题意舍去),x2=﹣3(不合题意舍去)或x1=1(不合题意舍去),x2=﹣(不合题意舍去);
当点P在AB之间时,
∵△PAM与△DD1A相似,
∴=或=,
∴=或=,
解得:x1=1(不合题意舍去),x2=﹣3(不合题意舍去)或x1=1(不合题意舍去),x2=﹣;
综上所述,点P的横坐标为﹣11或﹣或﹣;
②由①得,这样的点P共有3个.
15.如图1,经过原点O的抛物线y=ax2+bx(a≠0)与x轴交于另一点A(,0),在第一象限内与直线y=x交于点B(2,t).
(1)求这条抛物线的表达式;
(2)在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;
(3)如图2,若点M在这条抛物线上,且∠MBO=∠ABO,
①求点M的坐标;
②在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.
解:(1)∵B(2,t)在直线y=x上,
∴t=2,
∴B(2,2),
把A、B两点坐标代入抛物线解析式可得,解得,
∴抛物线解析式为y=2x2﹣3x;
(2)如图1,过C作CD∥y轴,交x轴于点E,交OB于点D,过B作BF⊥CD于点F,
∵点C是抛物线上第四象限的点,
∴可设C(t,2t2﹣3t),则E(t,0),D(t,t),
∴OE=t,BF=2﹣t,CD=t﹣(2t2﹣3t)=﹣2t2+4t,
∴S△OBC=S△CDO+S△CDB=CD•OE+CD•BF=(﹣2t2+4t)(t+2﹣t)=﹣2t2+4t,
∵△OBC的面积为2,
∴﹣2t2+4t=2,解得t1=t2=1,
∴C(1,﹣1);
(3)①设MB交y轴于点N,如图2,
∵B(2,2),
∴∠AOB=∠NOB=45°,
在△AOB和△NOB中,
∴△AOB≌△NOB(ASA),
∴ON=OA=,
∴N(0,),
∴可设直线BN解析式为y=kx+,
把B点坐标代入可得2=2k+,解得k=,
∴直线BN的解析式为y=x+,
联立直线BN和抛物线解析式可得,
解得(舍去)或,
∴M(﹣,),
②∵C(1,﹣1),
∴∠COA=∠AOB=45°,且B(2,2),
∴OB=2,OC=,
∵△POC∽△MOB,
∴==2,∠POC=∠BOM,
当点P在第一象限时,如图3,过M作MG⊥y轴于点G,过P作PH⊥x轴于点H,
∵∠COA=∠BOG=45°,
∴∠MOG=∠POH,且∠PHO=∠MGO,
∴△MOG∽△POH,
∴===2,
∵M(﹣,),
∴MG=,OG=,
∴PH=MG=,OH=OG=,
∴P(,);
当点P在第三象限时,如图4,过M作MG⊥y轴于点G,过P作PH⊥y轴于点H,
同理可求得PH=MG=,OH=OG=,
∴P(﹣,﹣);
综上可知存在满足条件的点P,其坐标为(,)或(﹣,﹣).
16.抛物线y=ax2+6x+c过A(2,3),B(4,3),C(6,﹣5)三点.
(1)求抛物线的表达式;
(2)如图①,抛物线上一点D在线段AC的上方,DE⊥AB,交AC于点E,若满足.求点D的坐标;
(3)如图②,F为抛物线顶点,过A作直线l⊥AB,若点P在直线l上运动,点Q在x轴上运动,是否存在这样的点P、Q,使得△BQP与△ABF相似(P与F为对应点),若存在,直接写出P、Q的坐标及此时△BQP的面积;若不存在,请说明理由.
解:(1)根据题意,设抛物线表达式为y=a(x﹣3)2+h.
把B(4,3),C(6,﹣5)代入得:,
解得:,
故抛物线的表达式为:y=﹣(x﹣3)2+4=﹣x2+6x﹣5;
(2)设直线AC的表达式为y=kx+n,
则,解得:,
∴直线AC的表达式为y=﹣2x+7,
设点D(m,﹣m2+6m﹣5)(2<m<6),则点E(m,﹣2m+7),
∴DE=(﹣m2+6m﹣5)﹣(﹣2m+7)=﹣m2+8m﹣12,
如图①,设直线DE与直线AB交于点G,
∵AG⊥EG,
∴AG=m﹣2,EG=3﹣(﹣2m+7)=2(m﹣2),
m﹣2>0,
在Rt△AEG中,
∴AE=(m﹣2),
由,则,
解得:m=3.5或2(舍去),
则D(,);
(3)存在,理由:
根据题意得:△ABF为等腰直角三角形,假设存在满足条件的点P、Q,则△BPQ为等腰直角三角形,
分三种情况:
①若∠BPQ=90°,BP=PQ,如图②,
过P作MN∥x轴,过Q作QM⊥MN于M,连接AB,
∵∠APB+∠QPA=90°,∠QPA+∠APM=90°,
∴∠APB=∠APM,
∵∠PAB=∠QMP=90°,PB=PQ,
∴△BAP≌△QMP(AAS),
∴AB=QM=2,PM=AP=3+2=5,
∴P(2,﹣2),Q(﹣3,0);
如图③,
同理可得:△BAP≌△PMQ(AAS),
∴AB=PM=2,AP=MQ=3﹣2=1,
∴P(2,2),Q(3,0);
②若∠BQP=90°,BQ=PQ,
如图④,过点Q作y轴的平行线交BA的延长线于点N,交过点P与x轴的平行线于点M,
同理可得:△BNQ≌△QMP(AAS),
∴NQ=PM=3,NG=PM﹣AG=3﹣2=1,
∴BN=MQ=4+1=5,
∴P(2,﹣5),Q(﹣1,0);
如图⑤,过点Q作y轴的平行线交AB的延长线于点N,交过点P与x轴的平行线于点M,
同理可得:△QNB≌△PMQ(AAS),
∴NQ=PM=3,
∴P(2,﹣1),Q(5,0),
③若∠PBQ=90°,BQ=BP,如图6,
过Q作QN⊥AB,交AB的延长线于N,
同理可得:△PAB≌△BNQ(AAS),
∵AB=2,NQ=3,AB≠NQ
∴此时不存在符合条件的P、Q.
综上,点P、Q的坐标分别为:(2,﹣2)、(﹣3,0);(2,2)、(3,0);(2,﹣5)、(﹣1,0);(2,﹣1)、(5,0).
17.如图,二次函数y=x2﹣3x的图象经过O(0,0),A(4,4),B(3,0)三点,以点O为位似中心,在y轴的右侧将△OAB按相似比2:1放大,得到△OA′B′,二次函数y=ax2+bx+c(a≠0)的图象经过O,A′,B′三点.
(1)画出△OA′B′,试求二次函数y=ax2+bx+c(a≠0)的表达式;
(2)点P(m,n)在二次函数y=x2﹣3x的图象上,m≠0,直线OP与二次函数y=ax2+bx+c(a≠0)的图象交于点Q(异于点O).
①求点Q的坐标(横、纵坐标均用含m的代数式表示)
②连接AP,若2AP>OQ,求m的取值范围;
③当点Q在第一象限内,过点Q作QQ′平行于x轴,与二次函数y=ax2+bx+c(a≠0)的图象交于另一点Q′,与二次函数y=x2﹣3x的图象交于点M,N(M在N的左侧),直线OQ′与二次函数y=x2﹣3x的图象交于点P′.△Q′P′M∽△QB′N,则线段NQ的长度等于 6 .
解:(1)由以点O为位似中心,在y轴的右侧将△OAB按相似比2:1放大,得==2
∵A(4,4),B(3,0)
∴A′(8,8),B′(6,0)
将O(0,0),A′(8,8),B′(6,0)代入y=ax2+bx+c
得
解得
∴二次函数的解析式为y=x2﹣3x;
(2)①∵点P在y=x2﹣3x的图象上,
∴n=m2﹣3m,
∴P(m,m2﹣3m),
设直线OP的解析式为y=kx
将点P代入,得mk=m2﹣3m,解得k=m﹣3,
∴OP:y=(m﹣3)x
∵直线OP与y=x2﹣3x交于点Q
∴x2﹣3x=(m﹣3)x,解得x1=0(舍),x2=2m,
∴Q(2m,2m2﹣6m)
②∵P(m,n)在二次函数y=x2﹣3x的图象上
∴n=m2﹣3m
∴P(m,m2﹣3m)
设直线OP的解析式为y=kx,将点P(m,m2﹣3m)代入函数解析式,
得mk=m2﹣3m
∴k=m﹣3
∴OP的解析是为y=(m﹣3)x
∵OP与y=x2﹣3x交于Q点
∴
解得(不符合题意舍去)
∴Q(2m,2m2﹣6m)过点P作PC⊥x轴于点C,过点Q作QD⊥x轴于点D
则OC=|m|,PC=|m2﹣3m|,OD=|2m|,QD=|2m2﹣6m|
∵==2
∴△OCP∽△ODQ
∴OQ=2OP
∵2AP>OQ
∴2AP>2OP,即AP>OP
∴>
化简,得m2﹣2m﹣4<0,解得1﹣<m<1+,且m≠0;
③P(m,m2﹣3m),Q(2m,2m2﹣6m)
∵点Q在第一象限,
∴,解得m>3
由Q(2m,2m2﹣6m),得QQ′的表达式是y=2m2﹣6m
∵QQ′交y=x2﹣3x交于点Q′
解得(不符合题意,舍)
∴Q′(6﹣2m,2m2﹣6m)
设OQ′的解析式为y=kx,(6﹣2m)k=2m2﹣6m
解得k=﹣m,OQ′的解析式为y=﹣mx,
∵OQ′与y=x2﹣3x交于点P′
∴﹣mx=x2﹣3x
解得x1=0(舍),x2=3﹣m
∴P′(3﹣m,m2﹣3m)
∵QQ′与y=x2﹣3x交于点P′
∴﹣mx=x2﹣3x
解得x1=0(舍去),x2=3﹣m
∴P′(3﹣m,m2﹣3m)
∵QQ′与y=x2﹣3x交于点M、N
∴x2﹣3x=2m2﹣6m
解得x1=,x2=
∵M在N左侧
∴M(,2m2﹣6m)
N(,2m2﹣6m)
∵△Q′P′M∽△QB′N
∴
∵,
化简得m2﹣12m+27=0
解得:m1=3(舍),m2=9
∴N(12,108),Q(18,108)
∴QN=6.
故答案为:6.
18.如图1,图形ABCD是由两个二次函数y1=kx2+m(k<0)与y2=ax2+b(a>0)的部分图象围成的封闭图形.已知A(1,0)、B(0,1)、D(0,﹣3).
(1)直接写出这两个二次函数的表达式;
(2)判断图形ABCD是否存在内接正方形(正方形的四个顶点在图形ABCD上),并说明理由;
(3)如图2,连接BC,CD,AD,在坐标平面内,求使得△BDC与△ADE相似(其中点C与点E是对应顶点)的点E的坐标.
解:(1)∵点A(1,0),B(0,1)在二次函数y1=kx2+m(k<0)的图象上,
∴,
∴,
∴二次函数解析式为y1=﹣x2+1,
∵点A(1,0),D(0,﹣3)在二次函数y2=ax2+b(a>0)的图象上,
∴,
∴,
∴二次函数y2=3x2﹣3;
(2)设M(m,﹣m2+1)为第一象限内的图形ABCD上一点,M'(m,3m2﹣3)为第四象限的图形上一点,
∴MM'=(1﹣m2)﹣(3m2﹣3)=4﹣4m2,
由抛物线的对称性知,若有内接正方形,
∴2m=4﹣4m2,
∴m=或m=(舍),
∵0<<1,
∴MM'=
∴存在内接正方形,此时其边长为;
(3)在Rt△AOD中,OA=1,OD=3,
∴AD==,
同理:CD=,
在Rt△BOC中,OB=OC=1,
∴BC==,
①如图1,当△DBC∽△DAE时,
∵∠CDB=∠ADO,
∴在y轴上存在E,由,
∴,
∴DE=,
∵D(0,﹣3),
∴E(0,﹣),
由对称性知,在直线DA右侧还存在一点E'使得△DBC∽△DAE',
连接EE'交DA于F点,作E'M⊥OD于M,连接E'D,
∵E,E'关于DA对称,
∴DF垂直平分EE',
∴△DEF∽△DAO,
∴,
∴,
∴DF=,EF=,
∵S△DEE'=DE•E'M=EF×DF=,
∴E'M=,
∵DE'=DE=,
在Rt△DE'M中,DM==2,
∴OM=1,
∴E'(,﹣1),
②如图2,
当△DBC∽△ADE时,有∠BDC=∠DAE,,
∴,
∴AE=,
当E在直线AD左侧时,设AE交y轴于P,作EQ⊥AC于Q,
∵∠BDC=∠DAE=∠ODA,
∴PD=PA,
设PD=n,
∴PO=3﹣n,PA=n,
在Rt△AOP中,PA2=OA2+OP2,
∴n2=(3﹣n)2+1,
∴n=,
∴PA=,PO=,
∵AE=,
∴PE=,
在AEQ中,OP∥EQ,
∴,
∴OQ=,
∵,
∴QE=2,
∴E(﹣,﹣2),
当E'在直线DA右侧时,
根据勾股定理得,AE==,
∴AE'=
∵∠DAE'=∠BDC,∠BDC=∠BDA,
∴∠BDA=∠DAE',
∴AE'∥OD,
∴E'(1,﹣),
综上,使得△BDC与△ADE相似(其中点C与E是对应顶点)的点E的坐标有4个,
即:(0,﹣)或(,﹣1)或(1,﹣)或(﹣,﹣2).
19.如图,直线y=x+2与x轴交于点A,与y轴交于点B,抛物线y=x2+bx+c经过点A,B.
(I)求抛物线的解析式;
(Ⅱ)M(m,0)为x轴上一个动点,过点M作直线MN垂直于x轴,与直线AB和抛物线分别交于点P、N.
①点M在线段OA上运动,若以B,P,N为顶点的三角形与△APM相似,求点M的坐标;
②点M在x轴上自由运动,若三个点M,P,N中恰有一点是其它两点所连线段的中点(三点重合除外),则称M,P,N三点为“共谐点”,请直接写出使得M,P,N三点成为“共谐点”的m的值.
解:
(1)∵y=x+2与x轴交于点A,与y轴交于点B,
∴当y=0时,x=3,即A(3,0).
∴当x=0时,y=2,即B(0,2).
∵抛物线y=x2+bx+c经过点A,B,
∴,
解得,
∴抛物线解析式为y=﹣x2+x+2;
(2)①由(1)可知直线解析式为y=﹣x+2,
∵M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N,
∴P(m,﹣m+2),N(m,﹣m2+m+2),
∴PM=﹣m+2,AM=3﹣m,PN=﹣m2+m+2﹣(﹣m+2)=﹣m2+4m,
∵△BPN和△APM相似,且∠BPN=∠APM,
∴∠BNP=∠AMP=90°或∠NBP=∠AMP=90°,
当∠BNP=90°时,则有BN⊥MN,
∴N点的纵坐标为2,
∴﹣m2+m+2=2,解得m=0(舍去)或m=,
∴M(,0);
当∠NBP=90°时,过点N作NC⊥y轴于点C,
则∠NBC+∠BNC=90°,NC=m,BC=﹣m2+m+2﹣2=﹣m2+m,
∵∠NBP=90°,
∴∠NBC+∠ABO=90°,
∴∠ABO=∠BNC,
∴Rt△NCB∽Rt△BOA,
∴=,
∴=,解得m=0(舍去)或m=,
∴M(,0);
综上可知当以B,P,N为顶点的三角形与△APM相似时,点M的坐标为(,0)或(,0);
②由①可知M(m,0),P(m,﹣m+2),N(m,﹣m2+m+2),
∵M,P,N三点为“共谐点”,
∴有P为线段MN的中点、M为线段PN的中点或N为线段PM的中点,
当P为线段MN的中点时,则有2(﹣m+2)=﹣m2+m+2,解得m=3(舍去)或m=0.5;
当M为线段PN的中点时,则有﹣m+2+(﹣m2+m+2)=0,解得m=3(舍去)或m=﹣1;
当N为线段PM的中点时,则有﹣m+2=2(﹣m2+m+2),解得m=3(舍去)或m=﹣;
综上可知当M,P,N三点成为“共谐点”时m的值为或﹣1或﹣.
20.如图,抛物线y=ax2+bx+c与x轴交于点A(﹣4,0)、B(1,0),与y轴交于点C(0,2).
(1)求抛物线的表达式;
(2)将△ABC绕AB中点E旋转180°,得到△BAD.
①求点D的坐标;
②判断四边形ADBC的形状,并说明理由;
(3)在该抛物线对称轴上是否存在点F,使△AEF与△BAD相似?若存在,求所有满足条件的F点的坐标;若不存在,请说明理由.
解:(1)将A(﹣4,0)、B(1,0)、C(0,2)代入y=ax2+bx+c,得:
,解得:,
∴抛物线的表达式为y=﹣x2﹣x+2.
(2)①过点D作DH⊥x轴于点H,如图1所示.
∵将△ABC绕AB中点E旋转180°,得到△BAD,
∴△ADH≌△BOC,
∴DH=OC=2,AH=BO=1,
∴OH=4﹣1=3,
∴点D的坐标为(﹣3,﹣2).
②四边形ADBC是矩形,理由如下:
∵将△ABC绕AB中点E旋转180°,得到△BAD,
∴AC=BD,AD=BC,
∴四边形ADBC是平行四边形.
∵A(﹣4,0),B(1,0),C(0,2),
∴AC=2,BC=,AB=5,
∴AC2+BC2=AB2,
∴△ACB是直角三角形,
∴∠ACB=90°,
∴四边形ADBC是矩形.
(3)∵A(﹣4,0)、B(1,0),
∴对称轴为直线x=﹣.
由题意可得:BD=2,AD=,
∴=.
当△AEF∽△ADB时,==,
∴=,
∴EF=5,
∴点F的坐标为(﹣,5)或(﹣,﹣5);
当△FEA∽△ADB时,==,
∴=,
∴EF=,
∴点F的坐标为(﹣,)或(﹣,﹣).
综上所述:点F的坐标为(﹣,5)或(﹣,﹣5)或(﹣,)或(﹣,﹣).
21.已知抛物线y=﹣x2+3x+4交y轴于点A,交x轴于点B,C(点B在点C的右侧).过点A作垂直于y轴的直线l.在位于直线l下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线l于点Q.连接AP.
(1)写出A,B,C三点的坐标;
(2)若点P位于抛物线的对称轴的右侧:
①如果以A,P,Q三点构成的三角形与△AOC相似,求出点P的坐标;
②若将△APQ沿AP对折,点Q的对应点为点M.是否存在点P,使得点M落在x轴上?若存在,求出点P的坐标;若不存在,请说明理由;
③设AP的中点是R,其坐标是(m,n),请直接写出m和n的关系式,并写出m的取值范围.
解:(1)∵令x=0,则y=4,
∴A(0,4);
∵令y=0,则﹣x2+3x+4=0,解得x1=4,x2=﹣1,
∴B(4,0),C(﹣1,0);
(2)①∵以A,P,Q三点构成的三角形与△AOC相似,
∴△AQP∽△AOC与△AQP∽△COA,
∴或,
即或,解得x=或x=7,均在对称轴的右侧,
∴P(,)或(7,﹣24);
②如图所示,过点M作y轴的平行线交直线AQ于点E,过点P作PF⊥直线ME于点F,
设Q(x,4),则P(x,﹣x2+3x+4),PQ=x2﹣3x=PM,
∵∠EAM+∠EMA=90°,∠EMA+∠FMP=90°,
∴∠FMP=∠EAM.
∵∠MFP=∠AEM=90°,
∴△AEM∽△MFP,
∴.
∵MP=x2﹣3x,
∴,
∴PF=4x﹣12,
∴OM=(4x﹣12)﹣x=3x﹣12,
在Rt△AOM中,
∵OM2+OA2=AM2,即(3x﹣12)2+42=x2,解得x1=4,x2=5均在抛物线对称轴的右侧,
∴P(4,0)或(5,﹣6).
③∵抛物线y=﹣x2+3x+4和A(0,4),
∴抛物线和直线l的交点坐标为A(0,4),(3,4),
设P(a,﹣a2+3a+4);∵A(0,4),
∴把y=4代入y=﹣x2+3x+4中,得,x=0或x=3,
∴a>3
∵AP的中点是R,A(0,4),
∴=m,=n,
∴n=﹣2m2+3m+4,
∵a>3,
∴2m>3,
∴m>.
22.如图,抛物线y=ax2+bx+2与x轴交于A、B两点,且OA=2OB,与y轴交于点C,连接BC,抛物线对称轴为直线x=,D为第一象限内抛物线上一动点,过点D作DE⊥OA于点E,与AC交于点F,设点D的横坐标为m.
(1)求点A的坐标与抛物线的表达式;
(2)连接CD,AD,设四边形OADC的面积为S.
①求S与m的关系式;
②当S最大时,求D点的坐标.
(3)若点P是对称轴上一点,当△DPF∽△BOC时,求m的值.
解:(1)∵OA=2OB,
∴设OB=t,OA=2t,则B(﹣t,0)、A(2t,0),
∵抛物线对称轴为直线x=,
∴=(﹣t+2t),
解得:t=1,
∴A(2,0)、B(﹣1,0),
把A(2,0)、B(﹣1,0)代入y=ax2+bx+2得:,
解得,
∴抛物线的表达式为y=﹣x2+x+2;
(2)当x=0时,y=2,
∴C(0,2),
∵D为第一象限内抛物线上一动点,点D的横坐标为m,
∴D(m,﹣m2+m+2),
①S=S△OCD+S△OAD
=×2×m+×2×(﹣m2+m+2)
=﹣m2+2m+2,
∴S与m的关系式为S=﹣m2+2m+2;
②∵S=﹣m2+2m+2=﹣(m﹣1)2+3,
∴当m=1时,S最大,此时D(1,2);
(3)设直线AC的解析式为y=kx+b,
把A(2,0),C(0,2)代入得:,
解得,
∴直线AC的解析式为y=﹣x+2,
设F(m,﹣m+2),P(,n),DF=﹣m2+2m,
∵△DPF∽△BOC,
∴∠DPF=∠BOC=90°,
∴,
由②得:n=m+1,
代入①得:(﹣m2+1)(2m﹣1)﹣(2m﹣1)2=0,
解得:m=或m=(舍去)或m=(舍去),
综上所述,m=.
专题58 二次函数中的面积问题(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用): 这是一份专题58 二次函数中的面积问题(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用),文件包含专题58二次函数中的面积问题原卷版docx、专题58二次函数中的面积问题解析版docx等2份试卷配套教学资源,其中试卷共63页, 欢迎下载使用。
专题57 二次函数中的线段最值问题(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用): 这是一份专题57 二次函数中的线段最值问题(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用),文件包含专题57二次函数中的线段最值问题原卷版docx、专题57二次函数中的线段最值问题解析版docx等2份试卷配套教学资源,其中试卷共57页, 欢迎下载使用。
专题55 一次函数背景下的图形存在性问题(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用): 这是一份专题55 一次函数背景下的图形存在性问题(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用),文件包含专题55一次函数背景下的图形存在性问题原卷版docx、专题55一次函数背景下的图形存在性问题解析版docx等2份试卷配套教学资源,其中试卷共119页, 欢迎下载使用。












