



- 专题11.1 一元一次不等式的应用(压轴题专项讲练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版) 试卷 1 次下载
- 专题11.2 不等式(组)与方程(组)的综合(压轴题专项讲练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版) 试卷 1 次下载
- 专题11.4 一元一次不等式(压轴题综合测试卷)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版) 试卷 1 次下载
- 专题13.2 期末复习选择压轴题专项训练(压轴题专项训练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版) 试卷 1 次下载
- 专题13.3 期末复习填空压轴题专项训练(压轴题专项训练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版) 试卷 1 次下载
专题13.1 期末复习解答压轴题专项训练(压轴题专项训练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版)
展开(1)如图 1,若DE∥OB,∠EDF=∠EFD,求x的值;
(2)如图 2,若DE⊥OA,是否存在这样的 x 的值,使得∠EFD=4∠EDF?若存在,求出 x的值;若不存在,说明理由.
(3)在(2)的条件下,若射线DA绕点D顺时针旋转至DO后立即回转,射线EO绕点E顺时针旋转至ED停止,射线DA转动的速度是4°/秒,射线EO转动的速度是1°/秒.若射线DA先旋转4秒,射线EO才开始绕点E顺时针旋转,在射线EO到达ED之前,射线EO旋转到第几秒时,射线DA与射线EO互相平行,直接写出答案.
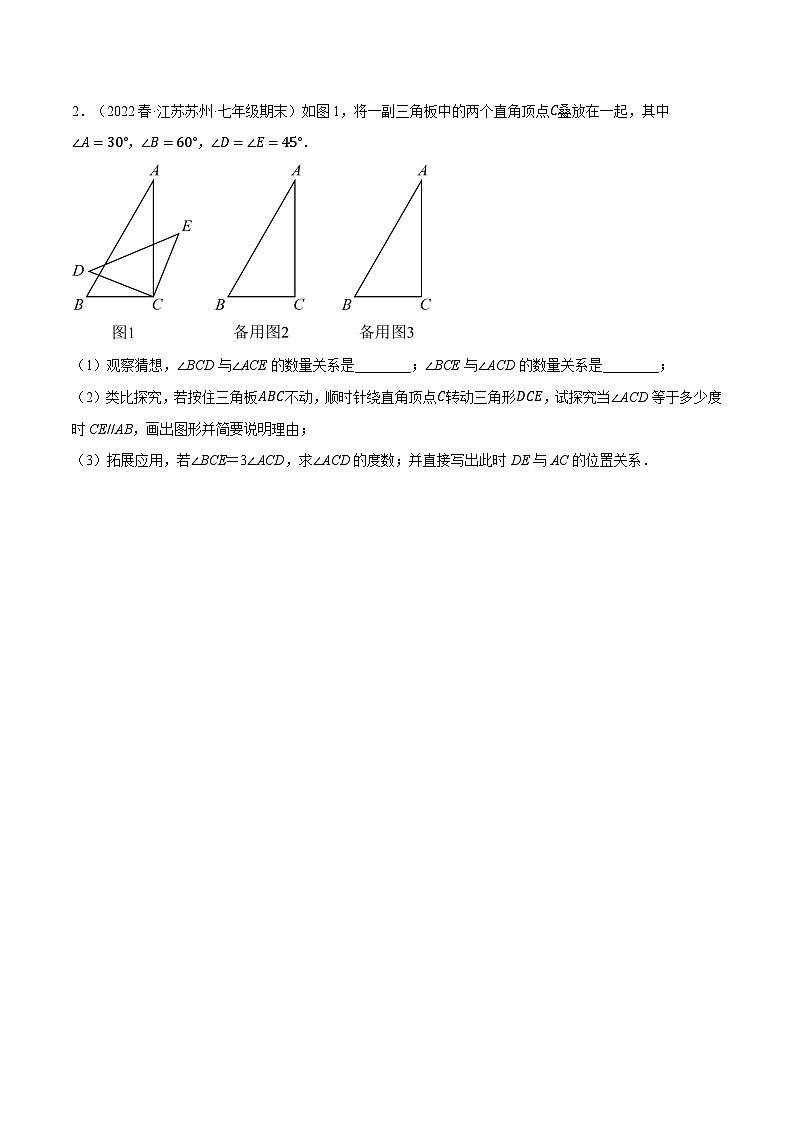
2.(2022春·江苏苏州·七年级期末)如图1,将一副三角板中的两个直角顶点C叠放在一起,其中∠A=30°,∠B=60°,∠D=∠E=45°.
(1)观察猜想,∠BCD与∠ACE的数量关系是________;∠BCE与∠ACD的数量关系是________;
(2)类比探究,若按住三角板ABC不动,顺时针绕直角顶点C转动三角形DCE,试探究当∠ACD等于多少度时CE//AB,画出图形并简要说明理由;
(3)拓展应用,若∠BCE=3∠ACD,求∠ACD的度数;并直接写出此时DE与AC的位置关系.
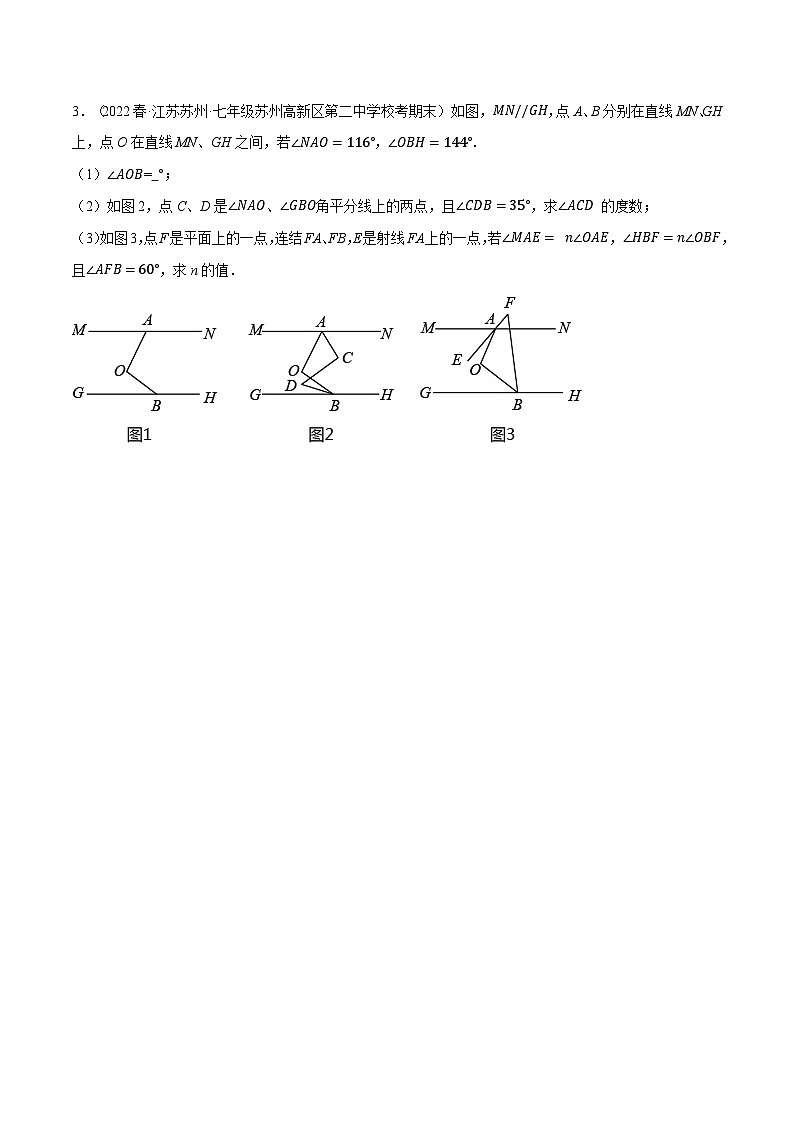
3.(2022春·江苏苏州·七年级苏州高新区第二中学校考期末)如图,MN//GH,点A、B分别在直线MN、GH上,点O在直线MN、GH之间,若∠NAO=116°,∠OBH=144°.
(1)∠AOB= °;
(2)如图2,点C、D是∠NAO、∠GBO角平分线上的两点,且∠CDB=35°,求∠ACD 的度数;
(3)如图3,点F是平面上的一点,连结FA、FB,E是射线FA上的一点,若∠MAE= n∠OAE,∠HBF=n∠OBF,且∠AFB=60°,求n的值.
4.(2022春·江苏淮安·七年级统考期末)【概念认识】如图①所示,在∠ABC中,若∠ABD=∠DBE=∠EBC,则BD,BE叫做∠ABC的“三分线”,其中,BD是“邻AB三分线”,BE是“邻BC三分线”.
【问题解决】
(1)如图②所示.在△ABC中.∠A=80°,∠ABC=45°.若∠ABC的三分线BD交AC于点D.求∠BDC的度数.
(2)如图③所示,在△ABC中.BP,CP分别是∠ABC的邻BC三分线和∠ACB的邻BC三分线,且∠BPC=140°.求∠A的度数.
【延伸推广】
(3)在△ABC中,∠ACD是△ABC的外角,∠ABC的三分线所在的直线与∠ACD的三分线所在的直线交于点P,若∠A=m°m>54,∠ABC=54°.求出∠BPC的度数.(用含m的式子表示)
5.(2022春·江苏扬州·七年级校联考期末)“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了A,D两座可旋转探照灯.假定主道路是平行的,即PQ∥CN,A,B为PQ上两点,AD平分∠CAB交CN于点D,E为AD上一点,连接BE,AF平分∠BAD交BE于点F.
(1)若∠C=40°,求∠EAP的大小;
(2)作AG交CD于点G,且满足∠1=13∠ADC,当∠2+65∠GAF=180°时,试说明:AC∥BE;
(3)在(1)问的条件下,探照灯A、D照出的光线在铁路所在平面旋转,探照灯射出的光线AC以每秒4度的速度逆时针转动,探照灯D射出的光线DN以每秒12度的速度逆时针转动,光线DN转至射线DC后立即以相同速度顺时针回转,若它们同时开始转动,设转动时间为t秒,当光线DN回到出发时的位置时同时停止转动,则在转动过程中,t为何值时光线AC与光线DN互相平行或垂直,请直接写出t的值.
6.(2022春·江苏宿迁·七年级统考期末)如图,在△ABC中,点D在AB上,过点D作DE∥BC,交AC于点E,DP平分∠ADE,交∠ACB的平分线于点P,CP与DE相交于点G,∠ACF的平分线CQ与DP相交于点Q.
(1)若∠A=50°,∠B=60°,则∠DPC=____________°,∠Q=____________°;
(2)若∠A=50°,当∠B的度数发生变化时,∠DPC、∠Q的度数是否发生变化?并说明理由;
(3)若∠A=x°,则∠DPC=____________°,∠Q=____________°;(用含x的代数式表示);
(4)若△PCQ中存在一个内角等于另一个内角的三倍,请直接写出所有符合条件的∠A的度数.
7.(2022春·江苏扬州·七年级统考期末)如图1,已知直线MN//PQ,直线GH分别与MN、PQ交于点H、G,∠1=140°,一块直角三角板ABC,其中∠CAB=30°,∠C=90°,它的斜边AB落在直线GH上,且点A与点G重合.
(1)求∠CAQ的度数;
(2)将三角板沿着射线GH方向平移,平移后的三角形A′B′C′.
①如图2,当点C′落在∠1的角平分线上时,求∠A′C′H的度数;
②如图3,当边A′C′与直线MN相交于点D,分别作∠MDA′与∠DA′G的角平分线DE、A′E相交于点E,求∠E的度数;
③请你直接写出当△A′C′H为直角三角形时,求∠NHC′的度数.
8.(2022春·江苏南京·七年级统考期末)如图,已知MN//GH,点A在MN上,点B、C在GH上.在△ABC中,∠ACB=90°,∠BAC=45°.点D、E在直线AB上,在△DEF中,∠DFE=90°,∠EDF=30°.
(1)图中∠BAN的度数是______°;
(2)将△DEF沿直线AB平移,如图2所示,当点F在MN上时,求∠AFE的度数;
(3)将△DEF沿直线AB平移,当以A、D、F为顶点的三角形中,有两个角相等时,请直接写出∠FAN的度数.
9.(2022春·江苏南京·七年级统考期末)【概念认识】
如图①,在∠ABC中,若∠ABD=∠DBE=∠EBC,则BD,BE叫做∠ABC的“三分线”.其中,BD是“邻AB三分线”,BE是“邻BC三分线”.
(1)【问题解决】
如图②,在△ABC中,∠A=70°,∠B=45°,若∠B的三分线BD交AC于点D,则∠BDC=____________°;
(2)如图③,在△ABC中,BP、CP分别是∠ABC邻AB三分线和∠ACB邻AC三分线,且BP⊥CP,求∠A的度数;
(3)【延伸推广】
如图,直线AC、BD交于点O,∠ADB的三分线所在的直线与∠ACB的三分线所在的直线交于点P.若∠A=66°,∠B=45°,∠ADB=m°,直接写出∠DPC的度数.
10.(2022春·江苏镇江·七年级统考期末)【问题情境】在△ABC中,∠ABC=n°(0
(1)∠EDF+∠FGB=_______°;
(2)∠FGB−∠AFD=_______°;
【类比研究】如图,当点F在线段AE上,点G在线段BC上时:
(3)∠EDF与∠FGB之间满足的数量关系为_______;
(4)∠FGB−∠AFD=_______°(用含n的代数式表示);
【深入探究】当点F在线段AE上,点G在线段CB的延长线上时,在下图中画出满足条件的示意图,并解决下列问题:
(5)∠EDF与∠FGB之间满足的数量关系为________;
(6)∠FGB与∠AFD之间满足的数量关系为________(用含n的代数式表示).
11.(2022春·江苏连云港·七年级校考期末)如图1,△ABC的外角平分线交于点F.
(1)若∠A=40°,则∠F的度数为 ;
(2)如图2,过点F作直线MN∥BC,交AB,AC延长线于点M,N,若设∠MFB=α,∠NFC=β,则∠A与α+β的数量关系是 ;
(3)在(2)的条件下,将直线MN绕点F转动.
①如图3,当直线MN与线段BC没有交点时,试探索∠A与α,β之间的数量关系,并说明理由;
②当直线MN与线段BC有交点时,试问①中∠A与α,β之间的数量关系是否仍然成立?若成立,请说明理由;若不成立,请给出三者之间的数量关系.
12.(2022春·江苏扬州·七年级统考期末)如图,已知点E在四边形ABCD的边BC的延长线上,BM、CN分别是∠ABC、∠DCE的角平分线,设∠BAD=α,∠ADC=β.
(1)如图1,若α+β=180°,判断BM、CN的位置关系,并说明理由:
(2)如图2,若α+β>180°,BM、CN相交于点O.
①当α=70°,β=150°时,则∠BOC=_______;
②∠BOC与α、β有怎样的数量关系?说明理由.
(3)如图3,若α+β<180°,BM、CN的反向延长线相交于点O,则∠BOC=______.(用含α、β的代数式表示).
13.(2022春·江苏盐城·七年级统考期末)如图1,△ABC中,∠ACB=90°,∠B=30°,AD是角平分线,点E、F分别在边AC、BC上,∠CEF=45°,CF
(2)在旋转一周过程中,试探究:当CE旋转多少度时,△AMN中有两个角相等.
14.(2022春·江苏南京·七年级统考期末)【概念认识】
在四边形ABCD中,∠A=∠B,如果在四边形ABCD内部或边AB上存在一点P,满足∠DPC=∠A,那么称点P是四边形ABCD的“映角点”.
【初步思考】
(1)如图①,在四边形ABCD中,∠A=∠B,点P在边AB上且是四边形ABCD的“映角点”.若DA//CP,DP//CB,则∠DPC的度数为________°.
(2)如图②,在四边形ABCD中,∠A=∠B,点P在四边形ABCD内部且是四边形ABCD的“映角点”,延长CP交边AB于点E.求证:∠ADP=∠CEB.
【综合运用】
(3)在四边形ABCD中,∠A=∠B=α,点P是四边形ABCD的“映角点”,DE、CF分别平分∠ADP、∠BCP,当DE和CF所在直线相交于点Q时,请直接写出∠CQD与α满足的关系及对应α的取值范围.
15.(2022春·江苏扬州·七年级统考期末)阅读感悟:有些关于方程组的问题,欲求的结果不是每一个未知数的值,而是关于未知数的一个代数式的值.如以下问题:已知实数x、y满足3x−y=5,2x+3y=7,求x−4y和7x+5y的值.本题常规思路是将3x−y=5①,2x+3y=7②联立组成方程组,解得x、y的值再代入欲求值的代数式得到答案.常规思路计算量比较大,其实本题还可以仔细观察两个方程未知数系数之间的关系,通过适当变形整体求得代数式的值,如由①-②可得x−4y=−2,由①+②×2可得7x+5y=19.这样的解题思想就是通常所说的“整体思想”.
解决问题:
(1)已知二元一次方程组2x+y=4x+2y=5,则x−y=______,x+y=______;
(2)试说明在关于x、y的方程组x+3y=4−ax−5y=3a中,不论a取什么实数,x+y的值始终不变;
(3)某班级组织活动购买小奖品,买3支铅笔、5块橡皮、1本笔记本共需21元,买4支铅笔、7块橡皮、1本笔记本共需28元,则购买10支铅笔、10块橡皮、10本笔记本共需多少元?
16.(2022春·江苏连云港·七年级统考期末)如图1,直线m与直线n相交于点O,A、B两点同时从点O出发,点A以每秒x个单位长度沿直线n向左运动,点B以每秒y个单位长度沿直线m向上运动.
(1)若运动1s时,点B比点A多运动1个单位;运动2s时,点B与点A运动的路程和为6个单位,则x=_________,y=_________.
(2)如图2,当直线m与直线n垂直时,设∠BAO和∠ABO的角平分线相交于点P.在点A、B在运动的过程中,∠APB的大小是否会发生变化?若不发生变化,请求出其值(写出主要过程);若发生变化,请说明理由.
(3)如图3,将(2)中的直线n不动,直线m绕点O按顺时针方向旋转α0<α<90,其他条件不变.
(i)用含有α的式子表示∠APB的度数_________.
(ii)如果再分别作△ABO的两个外角∠BAC,∠ABD的角平分线相交于点Q,并延长BP、QA交于点M.则下列结论正确的是_________(填序号).
①∠APB与∠Q互补;②∠M−∠Q为定值;③∠APB−∠M为定值;④∠Q与∠M互余.
17.(2022秋·江苏·七年级统考期末)点A对应数a,点B对应数b,点C对应数c,a6x﹣5y与﹣2x+15y的和是﹣6x5y.
(1)那么a= ,b= ,c= ;
(2)点P为数轴上一点,且满足PA=3PB+1,请求出点P所表示的数;
(3)点M为数轴上点A右侧一点,甲、乙两点分别从A、M出发,相向而行,2分钟后在途中相遇,相遇后,两点的速度都提高了1单位长度/分,当甲到达M点后立刻按原路向A返行,当乙到达A点后也立刻按原路向M点返行.甲、乙两点在第一次相遇后3分36秒又再次相遇,则A、M两点的距离是 单位长度;
(4)当甲以4单位长度/分的速度从A出发,向右运动,乙同时从点C出发,以6单位长度/分的速度向左运动,当甲到A、B、C的距离之和为40个单位长度时,假如甲立即掉头返行,请问甲、乙还能碰面吗?若能,求出碰面的地点对应的数;若不能,请说明理由.
18.(2022春·江苏盐城·七年级统考期末)【阅读感悟】
不等式x−ax−b>0可等价转化为不等式线x−a>0x−b>0或x−a<0x−b<0,不等式x−ax−b>0也可等价转化为不等式组x−a>0x−b>0或x−a<0x−b<0,我们把不等式x−ax−b>0与x−ax−b>0称为同解不等式.
【概念理解】
(1)下列属于同解不等式的是______;
①x+1x−2<0与x+1x−2≤0;②x−1x+2<0与x+1x−2<0;③x−2x+1≥0与x−2x+1≥0;④x−1x+2<0与x−1x+2<0.
【问题解决】
(2)解不等式:x−3x+2≤0;
【拓展延伸】
(3)不等式xx+1x−1<0的解是______.
19.(2022春·江苏镇江·七年级统考期末)【阅读理解】我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小,解决问题的策略一般都是进行一定的转化,其中“作差法”就是常用的方法之一.作差法:就是通过作差、变形,利用差的符号确定它们的大小.即要比较代数式A、B的大小,只要算A−B的值,若A−B>0,则A>B;若A−B=0,则A=B;若A−B<0,则A
①x+1_____x−3;
②当x>y时,3x+5y______2x+6y;
③若a
(3)【类比运用】图(1)是边长为4的正方形,将正方形一边保持不变,另一组对边增加2aa>0得到如图(2)所示的新长方形,此长方形的面积为S1;将正方形的边长增加a,得到如图(3)所示的新正方形,此正方形的面积为S2;则S1与S2大小的大小关系为:S1____S2;
(4)已知A=20016×20019,B=20017×20018,试运用上述方法比较A、B的大小,并说明理由.
20.(2022春·江苏镇江·七年级统考期末)小明的数学研学作业单上有这样一道题:已知−x+y=2,且x<3,y≥0,设w=x+y−2,那么w的取值范围是什么?
【回顾】
小明回顾做过的一道简单的类似题目:已知:−1
小明想:可以将研学单上的复杂问题转化为上面回顾的类似题目.
由−x+y=2得y=2+x,则w=x+y−2=x+2+x−2=2x,
由x<3,y≥0,得关于x的一元一次不等式组 ,
解该不等式组得到x的取值范围为 ,
则w的取值范围是 .
【应用】
(1)已知a﹣b=4,且a>1,b<2,设t=a+b,求t的取值范围;
(2)已知a﹣b=n(n是大于0的常数),且a>1,b≤1,2a+b的最大值为 (用含n的代数式表示);
【拓展】
若3x=6y+12=2z,且x>0,y≥−4,z≤9,设m=2x−2y−z,且m为整数,那么m所有可能的值的和为 .
专题13.3 期末复习填空压轴题专项训练(压轴题专项训练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版): 这是一份专题13.3 期末复习填空压轴题专项训练(压轴题专项训练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版),文件包含专题133期末复习填空压轴题专项训练压轴题专项训练苏科版原卷版docx、专题133期末复习填空压轴题专项训练压轴题专项训练苏科版解析版docx等2份试卷配套教学资源,其中试卷共42页, 欢迎下载使用。
专题13.2 期末复习选择压轴题专项训练(压轴题专项训练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版): 这是一份专题13.2 期末复习选择压轴题专项训练(压轴题专项训练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版),文件包含专题132期末复习选择压轴题专项训练压轴题专项训练苏科版原卷版docx、专题132期末复习选择压轴题专项训练压轴题专项训练苏科版解析版docx等2份试卷配套教学资源,其中试卷共58页, 欢迎下载使用。
专题10.3 方案选择问题(压轴题专项讲练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版): 这是一份专题10.3 方案选择问题(压轴题专项讲练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版),文件包含专题103方案选择问题压轴题专项讲练苏科版原卷版docx、专题103方案选择问题压轴题专项讲练苏科版解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。












