



- 专题11.3 一元一次不等式组的应用(压轴题专项讲练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版) 试卷 1 次下载
- 专题7.2 平行线中的常见模型(压轴题专项讲练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版) 试卷 1 次下载
- 专题7.3 平移中的几何综合(压轴题专项讲练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版) 试卷 1 次下载
- 专题7.4 与三角形有关线段的几何综合(压轴题专项讲练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版) 试卷 1 次下载
- 专题7.5 与三角形有关角的几何综合(压轴题专项讲练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版) 试卷 1 次下载
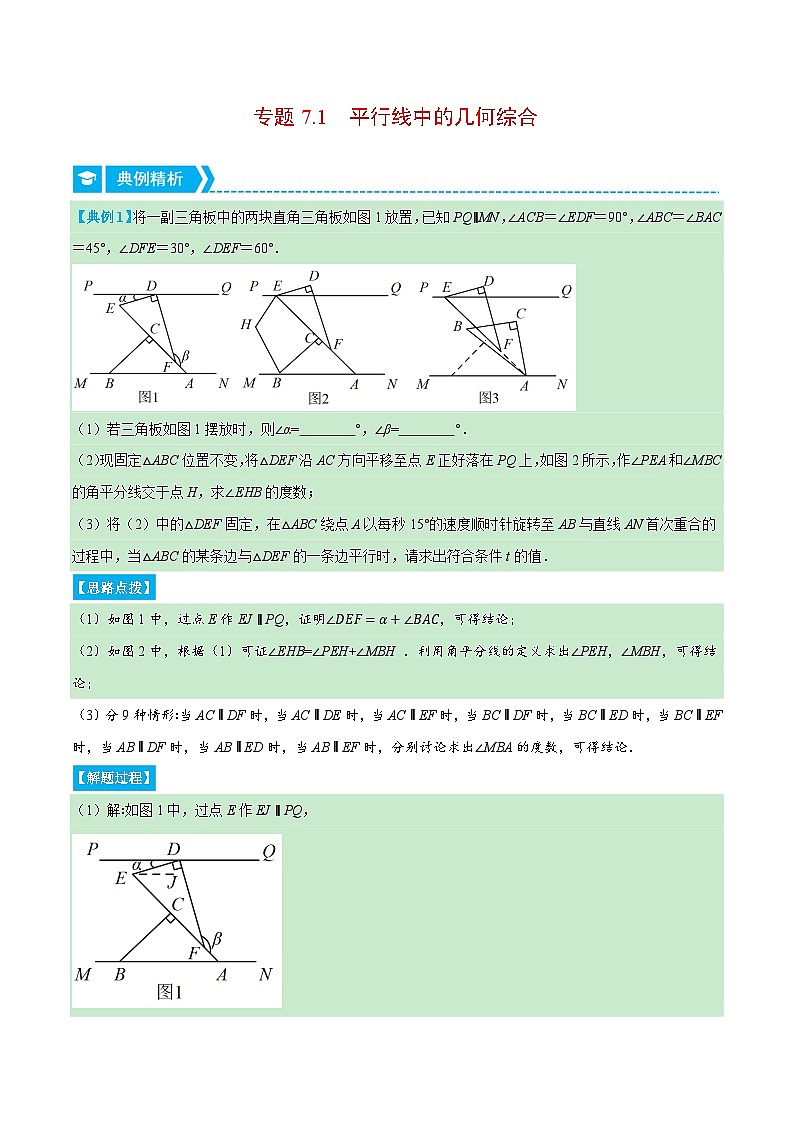
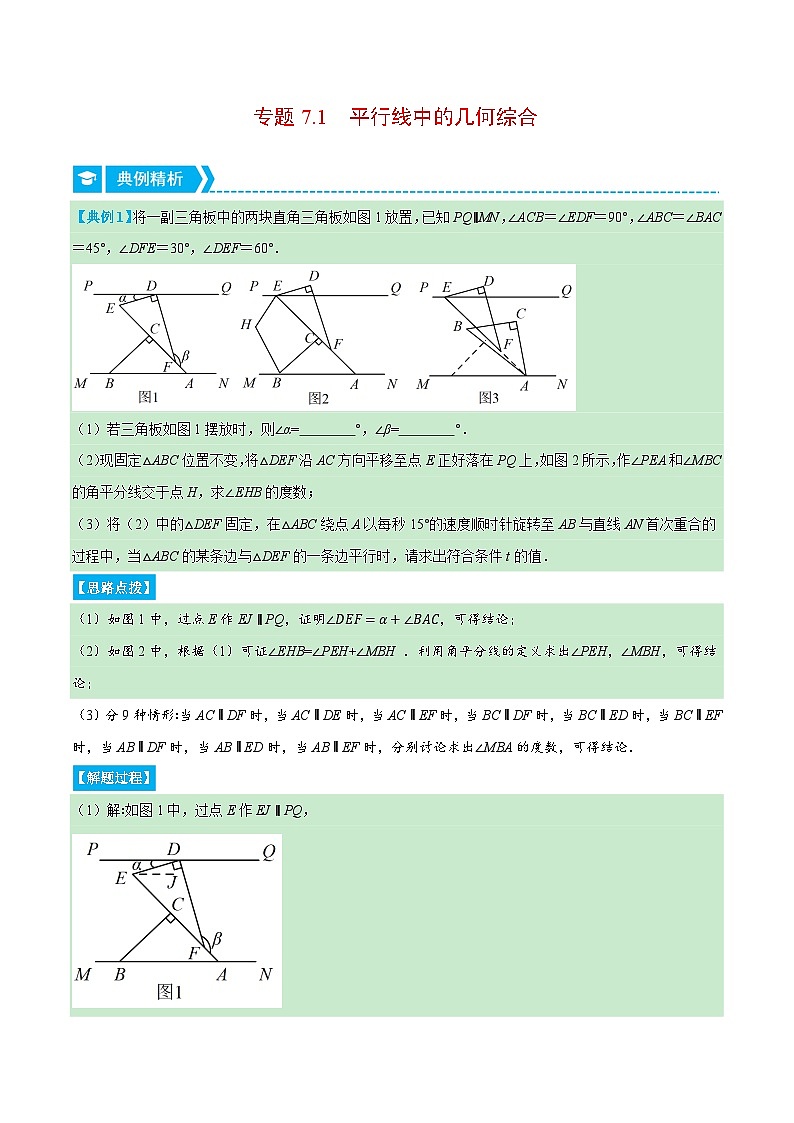
专题7.1 平行线中的几何综合(压轴题专项讲练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版)
展开【典例1】将一副三角板中的两块直角三角板如图1放置,已知PQ∥MN,∠ACB=∠EDF=90°,∠ABC=∠BAC=45°,∠DFE=30°,∠DEF=60°.
(1)若三角板如图1摆放时,则∠α= °,∠β= °.
(2)现固定△ABC位置不变,将△DEF沿AC方向平移至点E正好落在PQ上,如图2所示,作∠PEA和∠MBC的角平分线交于点H,求∠EHB的度数;
(3)将(2)中的△DEF固定,在△ABC绕点A以每秒15°的速度顺时针旋转至AB与直线AN首次重合的过程中,当△ABC的某条边与△DEF的一条边平行时,请求出符合条件t的值.
【思路点拨】
(1)如图1中,过点E作EJ∥PQ,证明∠DEF=α+∠BAC,可得结论;
(2)如图2中,根据(1)可证∠EHB=∠PEH+∠MBH .利用角平分线的定义求出∠PEH,∠MBH,可得结论;
(3)分9种情形∶当AC∥DF时,当AC∥DE时,当AC∥EF时,当BC∥DF时,当BC∥ED时,当BC∥EF时,当AB∥DF时,当AB∥ED时,当AB∥EF时,分别讨论求出∠MBA的度数,可得结论.
【解题过程】
(1)解∶如图1中,过点E作EJ∥PQ,
∵PQ∥MN, PQ∥EJ,
∴EJ∥MN,
∴∠α=∠DEJ,∠JEA=∠BAC=45°,
∴∠DEF=α+∠BAC,
∵∠DEF=60°,
∴α=60°−45°=15°,
∵∠DFE=30°,β+∠DFE=180°,
∴β=180°−30°=150°,
故答案为∶ 45, 150 ;
(2)解:如图2中,
利用(1)可证∠EHB=∠PEH+∠MBH .
∵PQ∥MN,
∴∠QEA=∠BAC=45° ,
∴∠AEP=180°-45°=135°,
∵∠CBA=45°,
∴∠CBM=180°-45°= 135*,
∵HE, HB分别平分∠AEP,∠CBM,
∴∠PEH=12∠PEA=67.5°,∠MBH=12∠FBM=67.5°,
∴∠EHB=∠PEH+∠MBH=135°;
(3)解:①当AC∥DF时,如图1,
易得此时BC∥ED ,
∵AC∥DF,易知E,F,A三点共线,∠DFE= ∠FAC=30°,
∴∠FAB=∠BAC-∠FAC=45-30°= 15°,∠BAM=∠FAM-∠FAB=45°-15°=30°,即15t=30,解得t=2;
②当AC∥DE时,如图2,
易得此时BC∥DF.过点A作AH∥BC,则AH∥ BC∥DF,
∴∠EAB=∠EAH+∠BAH=∠EFD+∠ABC=30°+45°=75°,
∴∠MAB=∠MAE+∠EAB=45°+75°=120°.
∴15t=120,
∴t=8,
③当AC∥EF时,情况不存在;④当BC∥DF时,同②;⑤当BC∥ED时,同①;
⑥当BC∥EF时,如图3,
此∠MAB=90°,即15t= 90,解得t=6;
⑦当AB∥DF时,如图4,
∵AB∥DF
∴∠BAF=∠DFE=30°,
∴∠MAB=∠MAF+∠BAF= 45°+30°=75°,即15t=75,解得t=5;
⑧当AB∥ED时,
∵AB∥ED,
∴∠FAB=180°-∠DEF=180°-60°=120°,
∴∠MAB=∠MAF+∠FAB=120°+45°=165°,
∴15t=165,
解得t=11;
⑨当AB∥EF时,此情况不存在.
综上所述,t的值为2或5或6或8或11.
1.(2022春·湖北武汉·七年级统考期末)直线AB∥CE,BE—EC是一条折线段,BP平分∠ABE.
(1)如图1,若BP∥CE,求证:∠BEC+∠DCE=180°;
(2)CQ平分∠DCE,直线BP,CQ交于点F.
①如图2,写出∠BEC和∠BFC的数量关系,并证明;
②当点E在直线AB,CD之间时,若∠BEC=40°,直接写出∠BFC的大小.
2.(2022春·河南安阳·七年级统考期末)猜想说理:
(1)如图,AB∥CD∥EF,分别就图1、图2、图3写出∠A,∠C,∠AFC的关系,并任选其中一个图形说明理由:
拓展应用:
(2)如图4,若AB∥CD,则∠A+∠C+∠AFC= 度;
(3)在图5中,若A1B∥AnD,请你用含n的代数式表示∠1+∠2+∠3+∠4+⋯+∠n的度数.
3.(2022春·四川广元·七年级统考期末)已知直线l1∥l2,直线l3和l1,l2分别交于C,D两点,点A,B分别在直线l1,l2上,且位于直线l3的右侧,动点P在直线l3上,且不和点C,D重合.
(1)如图1,当动点P在线段CD上运动时,求证:∠APB=∠CAP+∠DBP.
(2)如图2,当动点P在点C上方运动时(P,A,B不在同一直线上),请写出∠APB,∠CAP,∠DBP之间的数量关系,并说明理由.
(3)如图3,当动点P在点D下方运动时(P,A,B不在同一直线上),直接写出∠APB,∠CAP,∠DBP之间的数量关系.
4.(2022春·全国·七年级期末)已知:如图,AB∥CD,BG、FG 分别是∠AEF和∠CFE的角平分线,BG、FG交于点G.
(1)求证:∠BGF=90°;
(2)点M是直线AB上的动点,连接MG,过点G作GN⊥MG,交直线CD于点N,画出图形直线,写出∠MGE和∠NGF的数量关系 ;
(3)在(2)的条件下,当∠MGE=20°,∠AEG=40°时,求∠CNG的度数.
5.(2022春·重庆永川·七年级统考期末)已知:如图,AB∥CD.
(1)如图1,猜想并写出∠B、∠D、∠E之间的数量关系.以下图2、图3、图4是三种不同角度思考采用的不同添加辅助线的方式,请你选择其中的两种方式说明理由.
(2)在图4中,如果BE、DE分别平分∠ABD,∠CDB,则∠E的度数是多少?(直接写出答案)
(3)根据以上推理,直接写出图5、图6、图7中的∠B、∠D、∠E之间的数量关系.
6.(2022春·江苏扬州·七年级校联考阶段练习)如图,直线AB∥CD,直线EF与AB、CD分别交于点G、H,∠EHD=α(0°<α<90°).一个含30°角的直角三角板PMN中∠MPN=90°,∠PMN=60°.
(1)小安将直角三角板PMN按如图①放置,使点N、M分别在直线AB、CD上,且在点G、H的右侧,证明:∠PNB+∠PMD=∠MPN;
(2)若∠MNG的平分线NO交直线CD于点O,点N、M分别在直线AB、CD上,如图②.
①当NO∥EF,PM∥EF时,求α的度数;
②小安将三角板PMN保持PM∥EF并向左平移,请直接写出在平移的过程中∠MON的度数:∠MON=______(用含α的式子表示).
7.(2022春·上海宝山·七年级校考阶段练习)已知AB∥CD,点M为平面内的一点,∠AMD=90°.
(1)当点M在如图1的位置时,求∠MAB与∠D的数量关系(写出说理过程);
(2)当点M在如图2的位置时,则∠MAB与∠D的数量关系是 (直接写出答案);
(3)在(2)条件下,如图3,过点M作ME⊥AB,垂足为E,∠EMA与∠EMD的角平分线分别交射线EB于点F、G,回答下列问题(直接写出答案):图中与∠MAB相等的角是 ,∠FMG= 度.
8.(2022春·河北石家庄·七年级统考期中)【问题情景】(1)如图1,AB∥CD,∠PAB=140°,∠PCD=135°,求∠APC的度数;
【问题迁移】(2)如图2,已知∠MON,AD∥BC,点P在射线OM上运动,当点P在A,B两点之间运动时,连接PD,PC,∠ADP=∠α,∠BCP=∠β,求∠CPD与∠α,∠β之间的数量关系,并说明理由;
【知识拓展】(3)在(2)的条件下,若将“点P在A,B两点之间运动”改为“点P在A,B两点外侧运动(点P与点A,B,O三点不重合)”其他条件不变,请直接写出∠CPD与∠α,∠β之间的数量关系.
9.(2022春·辽宁大连·七年级校联考期中)已知直线AB∥CD,点E在直线AB、CD之间,点M、N分别在直线AB、CD上.
(1)如图1,直线GH过点E,分别与直线AB、CD交于点G、H,∠AME=∠GND,求证:∠NGH+∠MEH=180°;
(2)如图2,点F在直线CD上,ME、NE分别平分∠AMF、∠MNF,若∠FMN=2∠MEN,求∠MEN的度数;
(3)如图3,MQ平分∠AME,MH平分∠BME,GN平分∠ENC.直线GN与MH交于点H,NK平分∠END,NF∥MQ.求证:∠MHG=∠KNF.
10.(2022春·北京·七年级校考期中)“一带一路”让中国和世界联系更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视若灯A转动的速度是每秒2°,灯B转动的速度是每秒1°.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.
(1)填空:∠BAN=______°;
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)若两灯同时开始转动,两灯射出的光束交于点C,且∠ACB=120°,则在灯B射线到达BQ之前,转动的时间为______秒.
11.(2022春·浙江金华·七年级校联考阶段练习)如图1,已知MN∥PQ,,B在MN上,C在PQ上,A在B的左侧,D在C的右侧,DE平分∠ADC,BE平分∠ABC,直线DE,BE交于点E,∠CBN=120°.
(1)若∠ADQ=100°,求∠BED的度数;
(2)在图1中过点D作∠ADQ的角平分线与直线BE相交于点F,如图2,试探究∠DEB与∠DFE的关系;
(3)若改变线段AD的位置,使得点D在点C的左侧,其他条件不变,若∠ADQ=n°,过点D作∠PDA的角平分线与直线BE相交于点G,求∠BED+∠DGE的和是多少度?(用含n的代数式表示)
12.(2022春·北京海淀·七年级校考阶段练习)已知直线AB∥CD,点E,F分别在直线AB,CD上,∠EFD=α.点P是直线AB上的动点(不与E重合),连接PF,∠PEF和∠PFC的平分线所在直线交于点H.
(1)如图1,若EF⊥CD,点P在射线EB上.则当∠EPF=40°时,
∠EHF= °;
(2)如图2,若α=120°,点P在射线EA上.
①补全图形;
②探究∠EPF与∠EHF的数量关系,并证明你的结论.
(3)如图3,若0°<α<90°,直接写出∠EPF与∠EHF的数量关系(用含α的式子表示).
13.(2022秋·黑龙江哈尔滨·七年级校考阶段练习)如图1,AB∥CD,直线AB外有一点M,连接AM,CM.
(1)证明:∠M+∠A=∠C;
(2)如图2,延长MA至点E,连接CE,CM平分∠ECD,AF平分∠EAB,且AF与CM交于点F,求∠E与∠AFC的数量关系;
(3)如图3,在2的条件下,∠E=100°,FA⊥AN,连接CN,且∠M=2∠N,∠MCN=30°,求∠M的度数.
14.(2022秋·吉林长春·七年级长春市第四十五中学校考期末)已知AM∥CN,点B在直线AM、CN之间,∠ABC=88°.
(1)如图1,请直接写出∠A和∠C之间的数量关系:__________.
(2)如图2,∠A和∠C满足怎样的数量关系?请说明理由.
(3)如图3,AE平分∠MAB,CH平分∠NCB,AE与CH交于点G,则∠AGH的度数为__________.
15.(2022春·江西宜春·七年级江西省万载中学校考期中)在数学综合实践活动课上,老师让同学们以“两条平行直线AB,CD和一块含45°的直角三角板EFG(∠EFG=90°)”为背景,开展数学探究活动.如图,将三角板的顶点G放置在直线AB上.
(1)如图①,在GE边上任取一点P(不同于点G,E),过点P作CD//AB,且∠2=4∠1,求∠1的度数;
(2)如图②,过点E作CD//AB,请探索并说明∠AGF与∠CEF之间的数量关系;
(3)将三角板绕顶点G旋转,过点E作CD//AB,并保持点E在直线AB的上方.在旋转过程中,探索∠AGF与∠CEF之间的数量关系,并说明理由.
16.(2022秋·重庆渝中·七年级重庆巴蜀中学校考期末)已知,AB∥CD,直线FE交AB于点E,交CD于点F,点M在线段EF上,过M作射线MR、MP分别交射线AB、CD于点N、Q.
(1)如图1,当MR⊥MP时,求∠MNB+∠MQD的度数.
(2)如图2,若∠DQP和∠MNB的角平分线交于点G,求∠NMQ和∠NGQ的数量关系.
(3)如图3,当MR⊥MP,且∠EFD=60°,∠EMR=20°时,作∠MNB的角平分线NG.把一三角板OKI的直角顶点O置于点M处,两直角边分别与MR和MP重合,将其绕点O点顺时针旋转,速度为5°每秒,当OI落在MF上时,三角板改为以相同速度逆时针旋转.三角板开始运动的同时∠BNG绕点N以3°每秒的速度顺时针旋转,记旋转中的∠BNG为∠B′NG′,当NG′和NA重合时,整个运动停止.设运动时间为t秒,当∠B′NG′的一边和三角板的一直角边互相平行时,请直接写出t的值.
17.(2022秋·重庆·七年级重庆南开中学校考期末)已知,AE∥BD,∠A=∠D.
(1)如图1,判断AB与CD的位置关系,并说明理由;
(2)作∠BAE的平分线交CD于点F,点G为线段AB上一点,连接FG,∠CFG的平分线FM交线段AG于点H.如图2,若∠ECF=120°,∠AFH=20°,∠CFG=110°,求∠E的度数;
(3)如图3,连接AC,在(2)的条件下,将射线FG绕点F以5°每秒的速度逆时针旋转,旋转时间为t秒(0
(1)直接写出∠BPE与∠DQE的数量关系为____________________;
(2)如图2,∠APE的平分线PG和∠CQE的平分线QH的反向延长线相交于点G,求∠G的度数;
(3)如图3,M为线段PE上一点,连接QM,∠BPE和∠MQD的平分线相交于点N,直接写出∠PNQ和∠MQE的数量关系为____________________.
19.(2022春·四川成都·七年级校考期中)“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了A,D两座可旋转探照灯.假定主道路是平行的,即PQ//CN,A,B为PQ上两点,AD平分∠CAB交CN于点D,E为AD上一点,连接BE,AF平分∠BAD交BE于点F.
(1)若∠C=20°,则∠EAP=_______;
(2)作AG交CD于点G,且满足∠1=13∠ADC,当∠2+65∠GAF=180∘时,试说明:AC//BE;
(3)在(1)问的条件下,探照灯A、D照出的光线在铁路所在平面旋转,探照灯射出的光线AC以每秒5度的速度逆时针转动,探照灯D射出的光线DN以每秒15度的速度逆时针转动,DN转至射线DC后立即以相同速度回转,若它们同时开始转动,设转动时间为t秒,当DN回到出发时的位置时同时停止转动,则在转动过程中,当AC与DN互相平行或垂直时,请直接写出此时t的值.
20.(2022·全国·七年级假期作业)如图,直线PQ//MN,一副直角三角板△ABC,△DEF中,∠EDF=90°,∠ABC=∠BAC=45°,∠DFE=30°,∠DEF=60°.
(1)若△DEF如图1摆放,当ED平分∠PEF时,证明:FD平分∠EFM.
(2)若△ABC,△DEF如图2摆放时,则∠PDE=
(3)若图2中△ABC固定,将△DEF沿着AC方向平移,边DF与直线PQ相交于点G,作∠FGQ和∠GFA的角平分线GH、FH相交于点H(如图3),求∠GHF的度数.
(4)若图2中△DEF固定,(如图4)将△ABC绕点A顺时针旋转,2分钟转半圈,旋转至AC与直线AN首次重合的过程中,当线段BC与△DEF的一条边平行时,请求出旋转的时间.
专题11.2 不等式(组)与方程(组)的综合(压轴题专项讲练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版): 这是一份专题11.2 不等式(组)与方程(组)的综合(压轴题专项讲练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版),文件包含专题112不等式组与方程组的综合压轴题专项讲练苏科版原卷版docx、专题112不等式组与方程组的综合压轴题专项讲练苏科版解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。
专题10.3 方案选择问题(压轴题专项讲练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版): 这是一份专题10.3 方案选择问题(压轴题专项讲练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版),文件包含专题103方案选择问题压轴题专项讲练苏科版原卷版docx、专题103方案选择问题压轴题专项讲练苏科版解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。
专题9.1 整式的乘法(压轴题专项讲练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版): 这是一份专题9.1 整式的乘法(压轴题专项讲练)-2023-2024学年七年级数学下册压轴题专项高分突破(苏科版),文件包含专题91整式的乘法压轴题专项讲练苏科版原卷版docx、专题91整式的乘法压轴题专项讲练苏科版解析版docx等2份试卷配套教学资源,其中试卷共40页, 欢迎下载使用。












