2023-2024学年湖南省娄底市七年级（上）期末数学试卷（含解析）

这是一份2023-2024学年湖南省娄底市七年级（上）期末数学试卷（含解析），共15页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

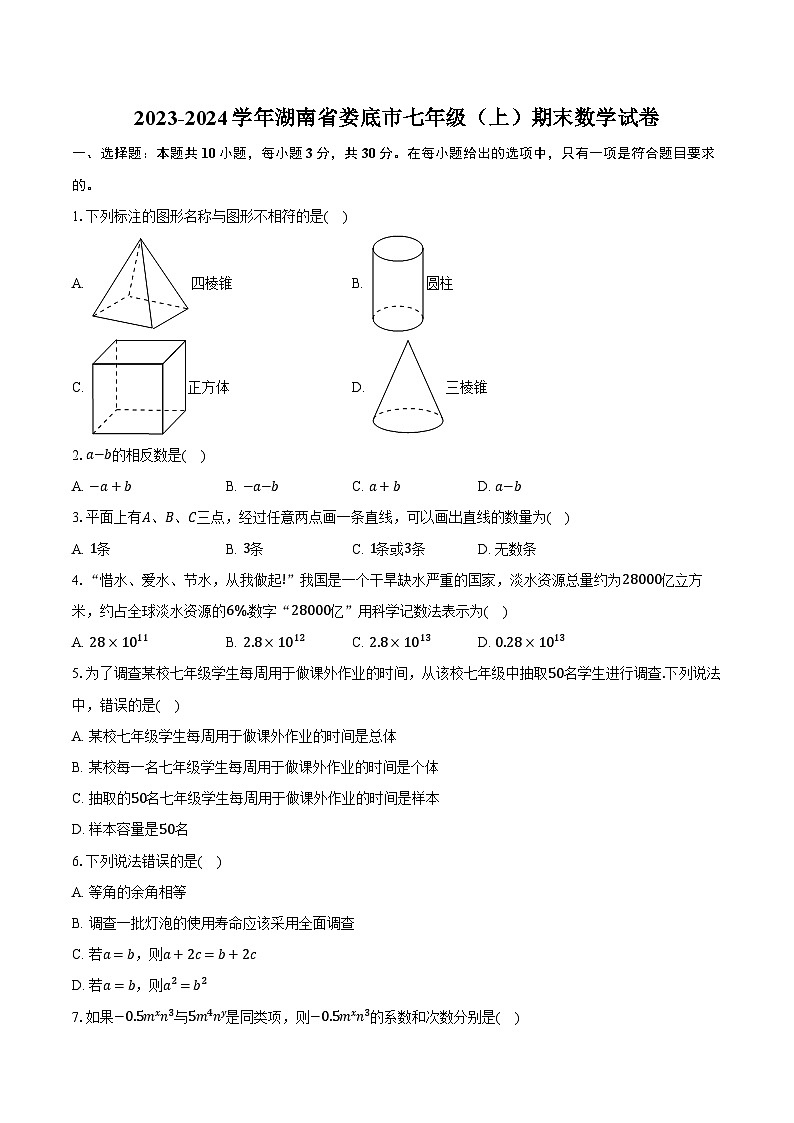
1.下列标注的图形名称与图形不相符的是( )
A. 四棱锥B. 圆柱
C. 正方体D. 三棱锥
2.a−b的相反数是( )
A. −a+bB. −a−bC. a+bD. a−b
3.平面上有A、B、C三点，经过任意两点画一条直线，可以画出直线的数量为( )
A. 1条B. 3条C. 1条或3条D. 无数条
4.“惜水、爱水、节水，从我做起!”我国是一个干旱缺水严重的国家，淡水资源总量约为28000亿立方米，约占全球淡水资源的6%.数字“28000亿”用科学记数法表示为( )
A. 28×1011B. 2.8×1012C. 2.8×1013D. 0.28×1013
5.为了调查某校七年级学生每周用于做课外作业的时间，从该校七年级中抽取50名学生进行调查.下列说法中，错误的是( )
A. 某校七年级学生每周用于做课外作业的时间是总体
B. 某校每一名七年级学生每周用于做课外作业的时间是个体
C. 抽取的50名七年级学生每周用于做课外作业的时间是样本
D. 样本容量是50名
6.下列说法错误的是( )
A. 等角的余角相等
B. 调查一批灯泡的使用寿命应该采用全面调查
C. 若a=b，则a+2c=b+2c
D. 若a=b，则a2=b2
7.如果−0.5mxn3与5m4ny是同类项，则−0.5mxn3的系数和次数分别是( )
A. −0.5，7B. −0.5，4C. 0.5，7D. 0.5，4
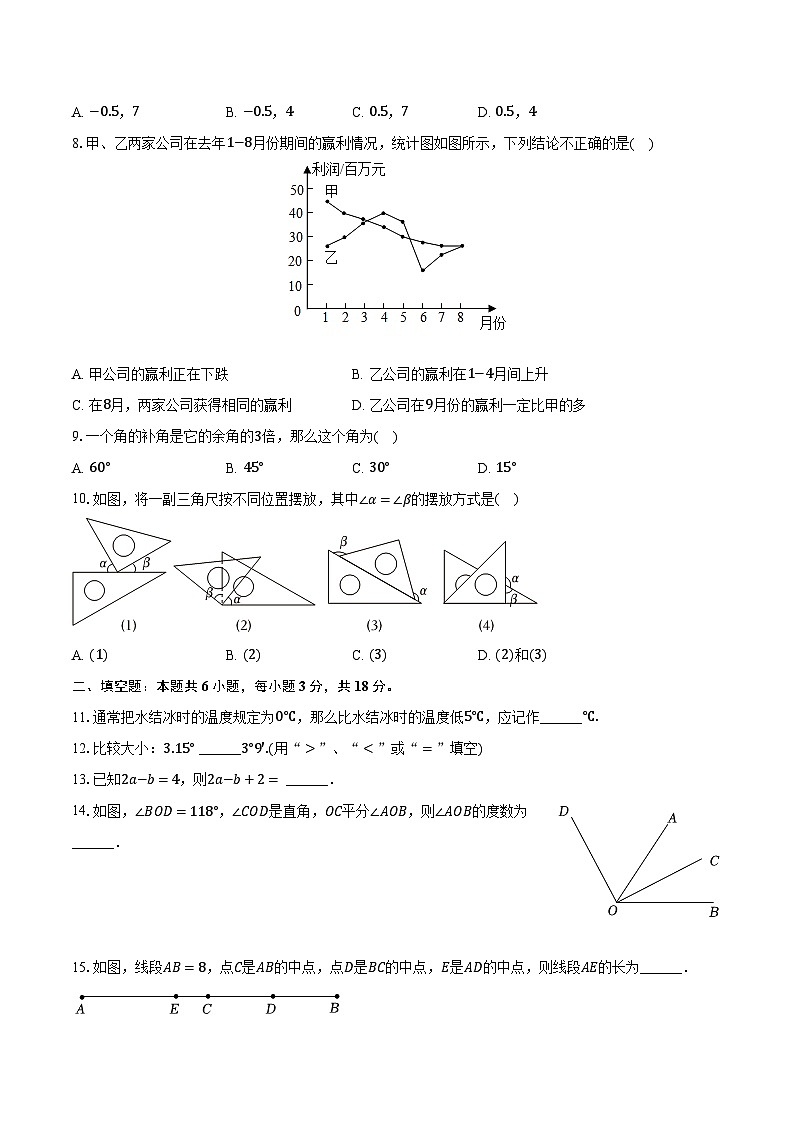
8.甲、乙两家公司在去年1−8月份期间的赢利情况，统计图如图所示，下列结论不正确的是( )
A. 甲公司的赢利正在下跌B. 乙公司的赢利在1−4月间上升
C. 在8月，两家公司获得相同的赢利D. 乙公司在9月份的赢利一定比甲的多
9.一个角的补角是它的余角的3倍，那么这个角为( )
A. 60°B. 45°C. 30°D. 15°
10.如图，将一副三角尺按不同位置摆放，其中∠α=∠β的摆放方式是( )
A. (1)B. (2)C. (3)D. (2)和(3)
二、填空题：本题共6小题，每小题3分，共18分。
11.通常把水结冰时的温度规定为0℃，那么比水结冰时的温度低5℃，应记作______℃.
12.比较大小：3.15° ______3°9′.(用“>”、“<”或“=”填空)
13.已知2a−b=4，则2a−b+2= ______．
14.如图，∠BOD=118°，∠COD是直角，OC平分∠AOB，则∠AOB的度数为______．
15.如图，线段AB=8，点C是AB的中点，点D是BC的中点，E是AD的中点，则线段AE的长为______．
16.观察下列图案，我们发现：围1个六边形需火柴6根，围2个六边形需火柴11根，围3个六边形需火柴16根，围4个六边形需火柴21根，….那么围n个六边形所需火柴的根数为(用含n的代数式表示)：______．
三、计算题：本大题共1小题，共6分。
17.先化简再求值：(4x2−2xy+y2)−3(x2−xy+5y2)，其中x=−1，y=−12．
四、解答题：本题共8小题，共66分。解答应写出文字说明，证明过程或演算步骤。
18.(本小题6分)
计算：(−3)4÷[2−(−7)]+4×(12−1)．
19.(本小题6分)
计算：2x−16−5x+18=1．
20.(本小题8分)
如图，在平面内有A，B，C三点．
(1)画出直线AB、射线AC和线段BC；
(2)在线段BC上任取一点D(不同于B，C)，连接AD，并延长AD至点E，使DE=2AD；(保留作图痕迹)
(3)数一数，图中有______条线段；
(4)AC+AB>CB，理由是______．
21.(本小题8分)
我省某地区结合本地自然条件，大力发展茶叶、蔗糖、水果、药材等产业，取得良好的经济效益，经过多年发展，茶叶、蔗糖、水果、药材成了该地区四大产业．图1，图2是根据该地区2006年各项产业统计资料绘制的两幅不完整统计图，请你根据统计图提供的信息解答：
(1)该地区2006年各项产业总产值共______万元；
(2)图1中蔗糖所占的百分数是______，2006年该地区蔗糖业的产值有______万元；
(3)将图2中“蔗糖”部分的图形补充完整．
22.(本小题9分)
现有树苗若干棵，计划栽在一段公路的一侧，要求路的两端各栽1棵，并且每2棵树的间隔相等.方案一：如果每隔5米栽1棵，则树苗缺21棵；方案二：如果每隔5.5米栽1棵，则树苗正好用完.设原有树苗x棵，请根据题意，解答下列问题：
(1)完善表格：
(2)求x的值；
(3)求这段路的长度．
23.(本小题9分)
如图，点O在直线AB上，∠COD=60°，∠AOE=2∠DOE．
(1)若∠BOD=60°，求∠COE的度数；
(2)试猜想∠BOD和∠COE的数量关系，并说明理由．
24.(本小题10分)
高斯是德国著名的数学家，上小学一年级时，老师出了一道数学题：1+2+3+…+100=？全班同学都在埋头计算时，小高斯却很快说出了正确答案：5050.小高斯的解答如下：原式=(1+100)+(2+99)+(3+98)+…+(50+51)=101×50=5050.人们把这样的求和公式称为高斯公式，即1+2+3+⋯+n=n(n+1)2，用语言描述为：和(首项+末项)×项数2.请解答下列问题：
(1)高斯的计算运用的运算律是______；
A.加法交换律
B.加法结合律
C.加法交换律和结合律
D.乘法分配律
(2)计算：−50−51−52−…−99−100；
(3)计算：1+3+5+…+2021+2023．
25.(本小题10分)
如图，数轴上点A对应的数为a，点B对应的数是b，且|a+5|+|b−15|=0.解答问题：
(1)a= ______；b= ______；
(2)A、B两点问的距离= ______；
(3)点M、N是数轴上的两个动点，点M以每秒3个单位长度的速度从点A出发，点N以每秒2个单位长度的速度从原点O出发.若M、N两点同时出发，都向数轴正方向运动：
①经过几秒，点M、点N到原点O的距离相等？
②当M、N两点运动到AM=3BN时，请直接写出点M在数轴上对应的数．
答案和解析
1.【答案】D
【解析】解：对于选项A，图形是四棱锥，故选项A中的名称与图形相符；
对于选项B，图形是圆柱，故选项B中的名称与图形相符；
对于选项C，图形是正方体，故选项C中的名称与图形相符；
对于选项D，图形是圆锥，故选项B中的名称与图形不相符．
故选：D．
根据四棱锥，圆柱，正方体，圆锥的定义及图形对各选项逐一进行判断即可得出答案．
此题主要考查了简单几何体的认识，正确识别四棱锥，圆柱，正方体，圆锥是解决问题的关键．
2.【答案】A
【解析】解：a−b的相反数是−(a−b)=−a+b，
故选：A．
符号不同，并且绝对值相等的两个数互为相反数，据此即可求得答案．
本题考查相反数，熟练掌握其定义是解题的关键．
3.【答案】C
【解析】解：①如果三点共线，过其中两点画直线，共可以画1条；
②如果任意三点不共线，过其中两点画直线，共可以画3条．
故选：C．
平面上有任意三点的位置关系有两种：①三点共线；②任意三点不共线，再确定直线的条数．
考查了直线、射线、线段，此类题没有明确平面上三点是否在同一直线上，需要运用分类讨论思想，解答时要分各种情况解答，要考虑到可能出现的所有情形，不要遗漏，否则讨论的结果就不全面．
4.【答案】B
【解析】解：28000亿=2800000000000=2.8×1012，
故选：B．
将一个数表示成a×10n的形式，其中1≤|a|<10，n为整数，这种记数方法叫做科学记数法，据此即可求得答案．
本题考查科学记数法表示较大的数，熟练掌握其定义是解题的关键．
5.【答案】D
【解析】解：A、某校七年级学生每周用于做课外作业的时间是总体，故A不符合题意；
B、某校每一名七年级学生每周用于做课外作业的时间是个体，故B不符合题意；
C、抽取的50名七年级学生每周用于做课外作业的时间是样本，故C不符合题意；
D、样本容量是50，故D符合题意；
故选：D．
根据总体，个体，样本，样本容量的意义，逐一判断即可解答．
本题考查了总体，个体，样本，样本容量，熟练掌握这些数学概念是解题的关键．
6.【答案】B
【解析】解：A、等角的余角相等，故A不符合题意；
B、调查一批灯泡的使用寿命应该采用抽样调查，故B符合题意；
C、若a=b，则a+2c=b+2c，故C不符合题意；
D、若a=b，则a2=b2，故D不符合题意；
故选：B．
根据全面调查与抽样调查，等式的性质，余角和补角，逐一判断即可解答．
本题考查了全面调查与抽样调查，等式的性质，余角和补角，熟练掌握这些数学概念是解题的关键．
7.【答案】A
【解析】解：∵−0.5mxn3与5m4ny是同类项，
∴x=4，y=3，
∴−0.5mxn3的系数是−0.5，次数为x+3=4+3=7，
故选：A．
先根据同类项的定义，求出x，y，然后根据单项式的系数是它的数字因数，次数是所有字母的指数和，进行解答即可．
本题主要考查了同类项和单项式的有关概念，解题关键是熟练掌握同类项、单项式的系数和次数的定义．
8.【答案】D
【解析】解：由折线统计图可以看出：甲1−8分的盈利的曲线呈下降趋势，因此盈利在逐月下跌，A的判定是正确的，
乙公司1−4月份盈利曲线是上升的，因此B的判定是正确的
8月时，甲、乙公司的盈利是一样的，因此C的判定是正确的，
9月的盈利很难取得谁的多、谁的少，不确定因此D的判定是错误的，
故选：D．
根据折线统计图中所反映的数据增减变化情况，这个做出判断即可，
考查从折线统计图中获取数据做出分析的能力，正确识图数据做出判断的前提和关键．
9.【答案】B
【解析】解：根据题意：设这个角为x，
则有180−x=3(90−x)，
解可得x=45°．
故选：B．
根据补角的定义计算．
本题考查补角的定义，和为180°的两角互为补角．
10.【答案】D
【解析】解：由所给图形可知，
图(1)中，α+β=180°−90°=90°，
所以(1)中的α与β互余．
图(2)中，α与β分别加上中间重叠部分的角都等于90°，
所以(2)中的α与β相等．
图(3)中，α+45°=180°=β+45°，
所以(3)中的α与β相等．
图(4)中，α+β=180°，
所以(4)中的α与β互补．
故选：D．
依次求出图中α与β之间的关系即可解决问题．
本题考查余角和补角，熟知余角和补角的定义是解题的关键．
11.【答案】−5
【解析】解：通常把水结冰时的温度规定为0℃，那么比水结冰时的温度低5℃，应记作−5℃，
故答案为：−5．
正数和负数是一组具有相反意义的量，据此即可求得答案．
本题考查正数和负数，理解具有相反意义的量是解题的关键．
12.【答案】=
【解析】解：3.15°=3°+0.15×60′=3°9′，
故答案为：=．
利用度分秒之间的进率将3.15°化为3°9′，进而得出答案．
本题考查度分秒的换算，熟练掌握度分秒之间的进率是解题的关键．
13.【答案】6
【解析】解：∵2a−b=4，
∴2a−b+2=4+2=6，
故答案为：6．
将已知数值代入原式计算即可．
本题考查代数式求值，将已知数值代入原式并进行正确的计算是解题的关键．
14.【答案】56°
【解析】解：∵∠BOD=118°，∠COD是直角，
∴∠BOC=∠BOD−∠COD=118°−90°=28°，
∵OC平分∠AOB，
∴∠AOB=2∠BOC=56°．
故答案为：56°．
由∠BOC=∠BOD−∠COD，即可得到∠BOC的度数，再由角平分线定义即可计算．
本题考查角的计算，关键是掌握角平分线定义．
15.【答案】3
【解析】解：∵AB=8，点C是AB的中点，
∴AC=BC=4，
∵点D是BC的中点，
∴CD=BD=2，
∴AD=AC+CD=6，
∵E是AD的中点，
∴AE=DE=3，
故答案为：3．
已知AB=8，点C是AB的中点，可得AC、BC的长，因为点D是BC的中点，可得CD、BD、AD的长，因为E是AD的中点，可得AE的长．
本题考查了两点间的距离，关键是掌握线段中点的定义．
16.【答案】5n+1
【解析】解：由所给图形可知，
围1个六边形所需的火柴根数为：6=1×5+1；
围2个六边形所需的火柴根数为：11=2×5+1；
围3个六边形所需的火柴根数为：16=3×5+1；
围4个六边形所需的火柴根数为：21=4×5+1；
…，
所以围n个六边形所需的火柴根数为(5n+1)根．
故答案为：5n+1．
依次求出图案中所需火柴的根数，发现规律即可解决问题．
本题考查图形变化的规律，能通过计算发现所需火柴的根数依次增加5是解题的关键．
17.【答案】解：原式=4x2−2xy+y2−3x2+3xy−15y2=x2+xy−14y2，
当x=−1，y=−12时，原式=1+12−72=−2．
【解析】原式去括号合并得到最简结果，把x与y的值代入计算即可求出值．
此题考查了整式的加减−化简求值，熟练掌握运算法则是解本题的关键．
18.【答案】解：(−3)4÷[2−(−7)]+4×(12−1)
=81÷9+4×(−12)
=9+(−2)
=7．
【解析】先算括号里面的，再算乘方，乘除，最后算加减即可．
本题考查的是有理数的混合运算，熟知有理数混合运算的法则是解题的关键．
19.【答案】解：去分母得，4(2x−1)−3(5x+1)=24，
去括号得，8x−4−15x−3=24，
移项得，8x−15x=24+3+4，
合并同类项得，−7x=31，
把x的系数化为1得，x=−317．
【解析】先去分母，再去括号，移项，合并同类项，把x的系数化为1即可．
本题考查的是解一元一次方程，熟知解一元一次方程的基本步骤是解答此题的关键．
20.【答案】8 两点之间，线段最短
【解析】解：(1)如图，直线AB，线段BC，射线AC即为所求；
(2)如图，线段AD和线段DE即为所求；
(3)图中的线段为AB，AC，AD，AE，DE，BD，CD，BC，共有8条线段．
故答案为：8；
(4)AC+AB>CB，理由是两点之间，线段最短，
故答案为：两点之间，线段最短..
(1)依据直线、射线、线段的定义，即可得到直线AB，射线AC，线段BC；
(2)依据在线段BC上任取一点D(不同于B，C)，连接线段AD，并延长AD至点E，使DE=2AD作图即可求解；
(3)根据线段的定义找出图中的线段即可；
(4)依据两点之间的距离分析即可．
本题主要考查了直线、射线、线段的定义，熟练掌握各定义是解题的关键．
21.【答案】5000 21% 1050
【解析】解：(1)该地区2006年各项产业总产值共1200÷24%=5000(万元)；
(2)蔗糖所占的百分数是1−30%−24%−10.6%−14.46%=21%，
2006年该地区蔗糖业的产值有5000×21%=1050(万元)．
(3)图2中“蔗糖”部分的图形补充如图：
(1)利用茶叶的产值及相应的百分比即可求出该地区2006年各项产业总产值；
(2)图1中蔗糖所占的百分数是1−30%−24%−10.6%−14.46%；利用总产值×蔗糖所占的百分比即可求出2006年该地区蔗糖业的产值；
(3)利用(2)中求出的数据即可将图补充完整．
本题考查的是条形统计图和扇形统计图的综合运用．读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图则能直接反映部分占总体的百分比大小．
22.【答案】x+21 5(x+21−1)
【解析】解：(1)完善表格如下：
故答案为：x+21，5(x+21−1)；
(2)5(x+21−1)=5.5(x−1)，
解得：x=211，
答：x的值为211；
(3)5×(211+21−1)=1155(米)，
答：这段路的长度1155米．
(1)根据题意可知，此题属于两端都栽的植树问题，间隔数=植树棵数−1，若相邻两树的间隔长称为一段，那么段数与应植树棵数的关系是：段数=植树棵数−1；已知相邻两树的间隔长，应植树棵数与路长的关系是：路长=(植树棵数−1)×间隔长；用x分别表示出路长，并填写表格即可；
(2)根据路长相等建立方程求出其解即可；
(3)结合(1)(2)列式计算即可．
此题考查了一元一次方程的应用，解答时由路的长度不变建立方程是关键．
23.【答案】解：(1)∵∠BOD=60°，
∴∠AOD=120°，
∵∠AOE=2∠DOE，
∴∠DOE=13∠AOD=40°，
∴∠COE=∠COD−∠DOE=60°−40°=20°；
(2)∠BOD=3∠COE，
设∠COE=x，则∠DOE=60−x，
∵∠AOE=2∠DOE，
∴∠AOD=3∠DOE=3(60−x)=180−3x，
∴∠BOD=180−∠AOD=180−(180−3x)=3x，
∴∠BOD=3∠COE．
【解析】(1)根据补角的定义可得∠AOD=120°，再根据角平分线的定义可得答案；
(2)设∠COE=x，则∠DOE=60−x，再利用AOE=2∠DOE，然后整理可得结论．
此题主要考查了邻补角、角平分线的定义，正确把握定义是解题关键．
24.【答案】C
【解析】解：(1)由高斯的计算过程可知，
他把加数的顺序进行了交换，
所以他运用了加法交换律；
他把所有的加数进行了两两结合相加，
所以他运用了加法结合律；
故选：C．
(2)根据高斯公式可知，
原式=−1−2−3−…−100−(−1−2−3−…−49)
=(−1−100)×1002−(−1−49)×492
=−5050−(−1225)
=−3825．
(3)根据高斯公式可知，
因为(2023+1)÷2=1012，
所以这列数有1012个．
则原式=(1+2023)×10122
=1024144．
(1)根据高斯计算的过程，发现他既用了加法的交换律，又用了加法的结合律．
(2)根据所给高斯公式即可解决问题．
(3)根据所给高斯公式即可解决问题．
本题考查数字变化的规律，理解题中所给的高斯公式是解题的关键．
25.【答案】−5 15 20
【解析】解：(1)∵|a+5|+|b−15|=0，
∴a+5=0，b−15=0，
解得a=−5，b=15；
故答案为：−5，15；
(2)∵|−5−15|=20，
∴A、B两点间的距离为20；
故答案为：20；
(3)设M，N运动时间为t秒，则M表示的数为−5+3t，N表示的数为2t，
①∵点M、点N到原点O的距离相等，
∴|−5+3t|=2t，
即−5+3t=2t或5−3t=2t，
解得t=5或t=1，
∴经过5秒或1秒，点M、点N到原点O的距离相等；
②∵AM=3BN，
∴3t=3|15−2t|，
解得t=5或t=15，
当t=5时，−5+3t=−5+15=10；
当t=15时，−5+3t=−5+45=40；
∴AM=3BN时，点M在数轴上对应的数为10或40．
(1)由|a+5|+|b−15|=0得a+5=0，b−15=0，可解得答案；
(2)由|−5−15|=20，知A、B两点间的距离为20；
(3)设M，N运动时间为t秒，则M表示的数为−5+3t，N表示的数为2t，
①根据点M、点N到原点O的距离相等，可得|−5+3t|=2t，即可解得答案；
②由AM=3BN，得3t=3|15−2t|，求出t值，即可得到答案．
本题考查一元一次方程的应用，解题的关键是用含t的代数式表示M，N所表示的数．方案
间隔长
应植树数
路长
方案一
5
______
______
方案
间隔长
应植树数
路长
方案一
5
x+21
5(x+21−1)