初中数学湘教版九年级下册2.2 圆心角、圆周角示范课ppt课件

这是一份初中数学湘教版九年级下册2.2 圆心角、圆周角示范课ppt课件，共26页。PPT课件主要包含了∠AOB＝∠COD，ABCD，前提在同圆中，前提在等圆中，①∠AOB∠COD，③ABCD，同样也可以得到，②∠AOB∠COD，③∠AOB∠COD，①ABCD等内容，欢迎下载使用。

1. 理解圆心角的概念.2.掌握圆心角，弧和弦的相关结论
在生活中像飞镖靶这样的圆形中，都存在着角，那么这些角有什么共同的特征呢？
顶点在圆心，角的两边与圆相交
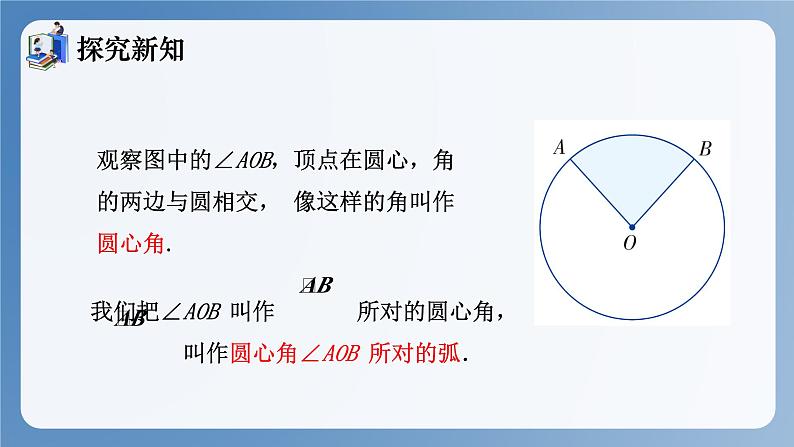
观察图中的∠AOB，顶点在圆心，角的两边与圆相交， 像这样的角叫作圆心角.
我们把∠AOB 叫作 所对的圆心角， 叫作圆心角∠AOB 所对的弧．
在生活中，我们常遇到圆心角，如飞镖靶中有圆心角，还有手表的时针与分针所成的角等也是圆心角．
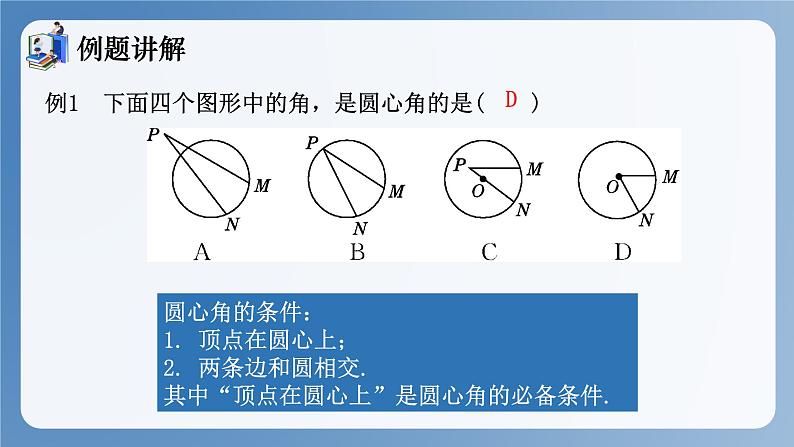
例1 下面四个图形中的角，是圆心角的是(　　)
圆心角的条件：1. 顶点在圆心上；2. 两条边和圆相交.其中“顶点在圆心上”是圆心角的必备条件.
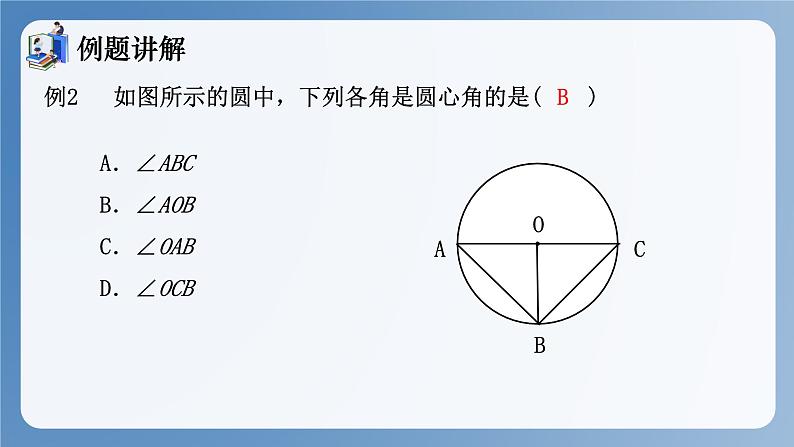
例2 如图所示的圆中，下列各角是圆心角的是(　　)
A．∠ABCB．∠AOBC．∠OABD．∠OCB
在同圆中，如果圆心角相等，那么它们所对的弧相等，所对的弦也相等．
例1 如果两个圆心角相等，那么 ( )A．这两个圆心角所对的弦相等B．这两个圆心角所对的弧相等C．这两个圆心角所对的弦和弧分别均相等D．以上说法都不对
如图，在⊙O中，将扇形AOB绕点O逆时针旋转某个角度到扇形COD的位置，那么，∠AOB与∠COD，AB与CD，弦AB与弦CD有怎样的数量关系？
在旋转过程中，∠AOB= ∠COD，AB=CD ，弦AB=弦CD.
如图，在等圆中，如果扇形AOB等于扇形COD，你发现的等量关系是否依然成立？
.
在同圆或等圆中，如果圆心角相等，那么它们所对的弧相等，所对的弦相等．
弧、弦与圆心角的关系定理
在同圆或等圆中，如果弧相等，那么它们所对的圆心角相等，所对的弦相等．
在同圆或等圆中，如果弦相等，那么它们所对的圆心角相等，所对的弧相等．
想一想：定理“在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等”中，可否把条件“在同圆或等圆中”去掉？为什么？
不可以，如图，如果丢掉了这个前提，即使圆心角相等，所对的弧、弦也不一定相等.
例2 下列说法中，正确的是(　　)A．等弦所对的弧相等B．等弧所对的弦相等C．在同圆中，圆心角相等，所对的弦相等D．弦相等，所对的圆心角相等
例3 如图，等边△ABC 的顶点 A，B，C在 ⊙O 上，求圆心角∠AOB 的度数 .
∴ AB = BC = CA.
∴ ∠AOB ＝ ∠BOC ＝ ∠AOC.
解：∵△ABC 是等边三角形 ,
又∵ ∠AOB+∠BOC+∠AOC = 360°.
1.如图，AB、CD是⊙O的两条弦．(1) 如果AB=CD，那么 ， ． (2)如果 ，那么 ， ．(3) 如果∠AOB=∠COD，那么 ， ．
(4) 如果AB=CD，OE⊥AB于E，OF⊥CD于F，OE与OF相等吗？为什么？
2. 如图，在⊙O中，AB 是直径，∠AOE = 60°，点 C，D 是 的三等分点，求∠COE 的度数.
解 ∵ ∠AOE = 60°， ∴∠BOE = 120°又∵点 C，D 是 的三等分点∴∠BOC = ∠COD = ∠DOE = 40°∴∠COE = 80°
解：CD = 2AB 不成立.理由如下： 取 中点 E ,连接 OE，CE，DE. 那么∠AOB = ∠COE = ∠DOE， 所以弦AB = CE = DE. 在△CDE中，CE+DE ＞CD，即CD＜2AB.
思路点拨：作D关于AB的对称点E，连接CE交AB于点P1,则若P在P1时，DP+CP最小，最小长度为EC.
弦、弧、圆心角的关系定理
1.教材P56第1、2题. 2.完成同步练习册中本课时的练习.