
(决胜高考)2024年高考数学立体几何初步小专题(8+3+3)特训
展开
这是一份(决胜高考)2024年高考数学立体几何初步小专题(8+3+3)特训,共4页。试卷主要包含了选择题,多项选择题,填空题等内容,欢迎下载使用。
一、选择题
1.已知m,n是两条不同的直线,α,β是两个不同的平面,下列说法正确的是( )
A.若m∥n,且n⊂α,则m∥αB.若m⊥n,且n⊂α,则m⊥α
C.若m∥α,且m∥β,则α∥βD.若m⊥α,且m⊥β,则α⊥β
2.一个圆锥的轴截面是边长为4的等边三角形,在该圆锥中有一个内接圆柱(下底面在圆锥底面上,上底面的圆周在圆锥侧面上),则当该圆柱侧面积取最大值时,该圆柱的高为( )
A.1B.2C.3D.3
3.将一个半径为2的球削成一个体积最大的圆锥,则该圆锥的内切球的半径为( )
A.3+13B.2(3+1)3C.2(3−1)3D.4(3−1)3
4.三棱锥A−BCD中,AC⊥平面BCD,BD⊥CD.若AB=3,BD=1,则该三棱锥体积的最大值为( )
A.2B.43C.1D.23
5.正四棱锥P−ABCD的底面边长为42,PA=45则平面PCD截四棱锥P−ABCD外接球所得截面的面积为( ).
A.100π9B.50π3C.200π9D.100π3
6.如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD),若M,O分别为线段A1C,DE的中点,则在△ADE翻转过程中,下列说法错误的是( )
A.与平面A1DE垂直的直线必与直线MB垂直
B.异面直线BM与A1E所成角是定值
C.一定存在某个位置,使DE⊥MO
D.三棱锥A1ADE外接球半径与棱AD的长之比为定值
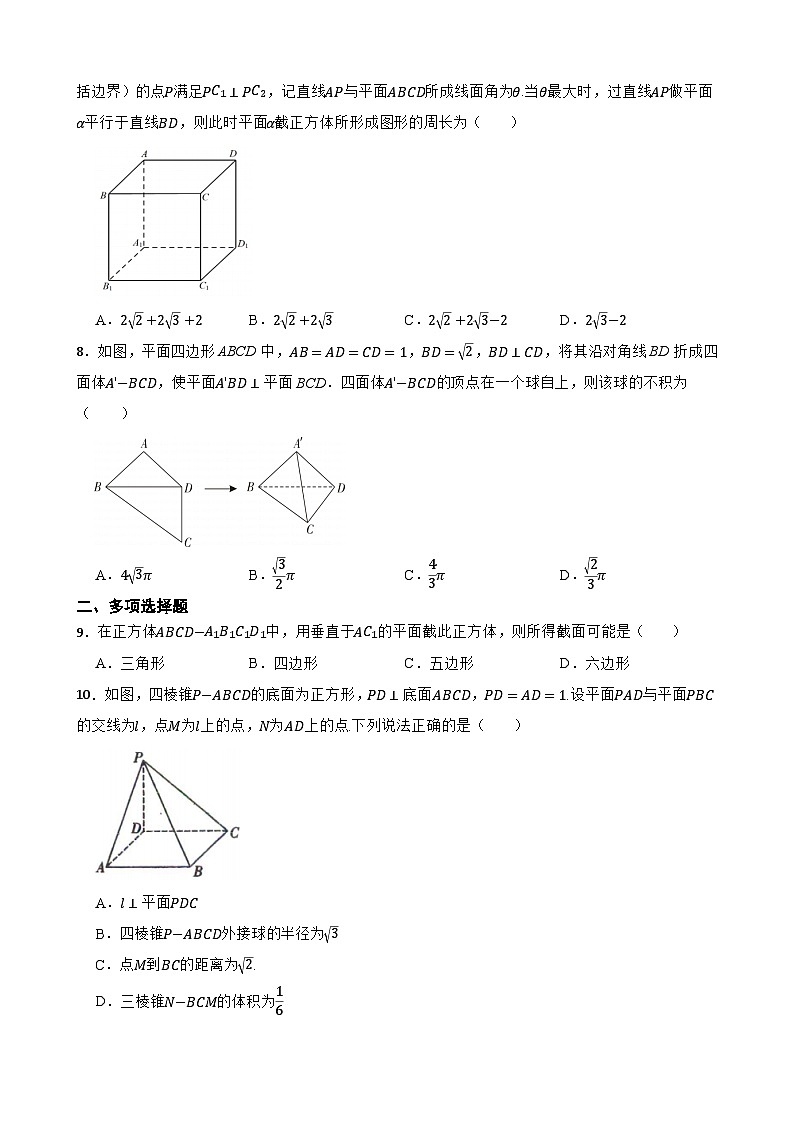
7.已知正方体ABCD−A1B1C1D1的边长为1,点C1关于平面ABCD对称的点为C2,矩形AA1CC1内(包括边界)的点P满足PC1⊥PC2,记直线AP与平面ABCD所成线面角为θ.当θ最大时,过直线AP做平面α平行于直线BD,则此时平面α截正方体所形成图形的周长为( )
A.22+23+2B.22+23C.22+23−2D.23−2
8.如图,平面四边形ABCD中,AB=AD=CD=1,BD=2,BD⊥CD,将其沿对角线BD折成四面体A′−BCD,使平面A′BD⊥平面BCD.四面体A′−BCD的顶点在一个球自上,则该球的不积为( )
A.43πB.32πC.43πD.23π
二、多项选择题
9.在正方体ABCD−A1B1C1D1中,用垂直于AC1的平面截此正方体,则所得截面可能是( )
A.三角形B.四边形C.五边形D.六边形
10.如图,四棱锥P−ABCD的底面为正方形,PD⊥底面ABCD,PD=AD=1.设平面PAD与平面PBC的交线为l,点M为l上的点,N为AD上的点.下列说法正确的是( )
A.l⊥平面PDC
B.四棱锥P−ABCD外接球的半径为3
C.点M到BC的距离为2.
D.三棱锥N−BCM的体积为16
11.数学中有许多形状优美、寓意独特的几何体,“勒洛四面体”就是其中之一.勒洛四面体是以正四面体的四个顶点为球心,以正四面体的棱长为半径的四个球的公共部分.如图,在勒洛四面体中,正四面体ABCD的棱长为4,则下列结论正确的是( )
A.勒洛四面体ABCD最大的截面是正三角形
B.勒洛四面体ABCD的体积大于正四面体ABCD的体积
C.勒洛四面体ABCD被平面ABC截得的截面面积是8(π−3)
D.勒洛四面体ABCD四个曲面所有交线长的和为8π
三、填空题
12. 已知四面体ABCD中,AB=AD=BC=DC=BD=5,AC=8,则四面体ABCD的体积为
13.三棱雉P−ABC的每一个面都是边长为1的正三角形,以它的高PH所在直线为旋转轴,将其旋转60°得到三棱雉P−A′B′C′,则两个三棱雉公共区域的体积为 .
14.如图,在棱长为1的正方体ABCD−A1B1C1D1中,E是棱AA1上的一个动点,给出下列四个结论:
①三棱锥B1−BED1的体积为定值;
②存在点E使得B1D⊥平面BED1;
③D1E+BE的最小值为2+1;
④对每一个点E,在棱DC上总存在一点P,使得AP∥平面BED1;
⑤M是线段BC1上的一个动点,过点A1的截面α垂直于DM,则截面α的面积的最小值为62.
其中正确的命题的序号是 .
答案解析部分
1.【答案】D
2.【答案】D
3.【答案】D
4.【答案】D
5.【答案】C
6.【答案】C
7.【答案】C
8.【答案】B
9.【答案】A,D
10.【答案】A,C,D
11.【答案】B,C
12.【答案】10113
13.【答案】218
14.【答案】①⑤
相关试卷
这是一份(决胜高考)2024年高考数学函数的应用小专题(8+3+3)特训,共4页。试卷主要包含了选择题,多项选择题,填空题等内容,欢迎下载使用。
这是一份冲刺2024年高考数学:数列小专题特训,共8页。试卷主要包含了单选题,多选题,填空题等内容,欢迎下载使用。
这是一份冲刺2024年高考数学:平面向量小专题特训,共11页。试卷主要包含了单选题,多选题,填空题等内容,欢迎下载使用。









