


还剩16页未读,
继续阅读
所属成套资源:沪科版八年级数学下册 【精品教学课件】
成套系列资料,整套一键下载
沪科版八年级数学下册 第19章 四边形 第2课时 矩形的判定(课件)
展开
这是一份沪科版八年级数学下册 第19章 四边形 第2课时 矩形的判定(课件),共24页。
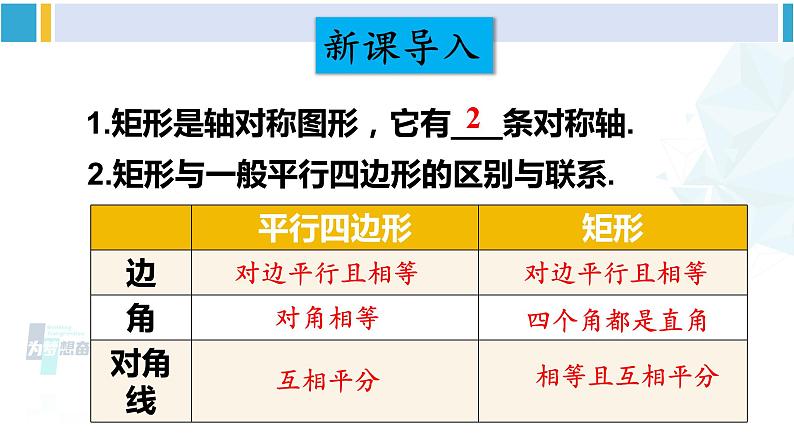
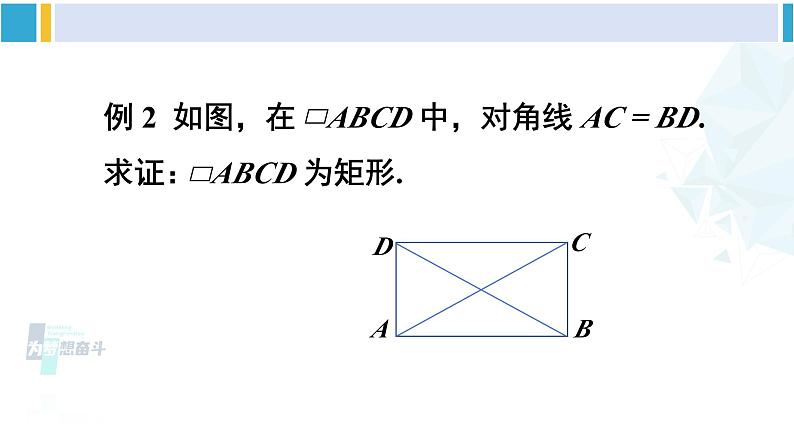
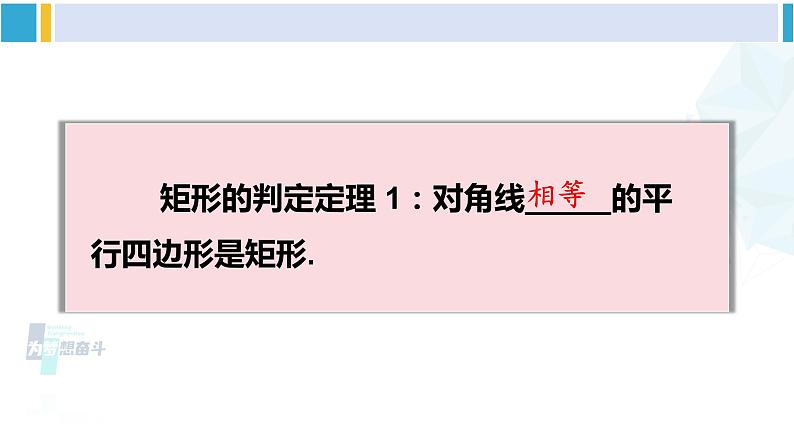
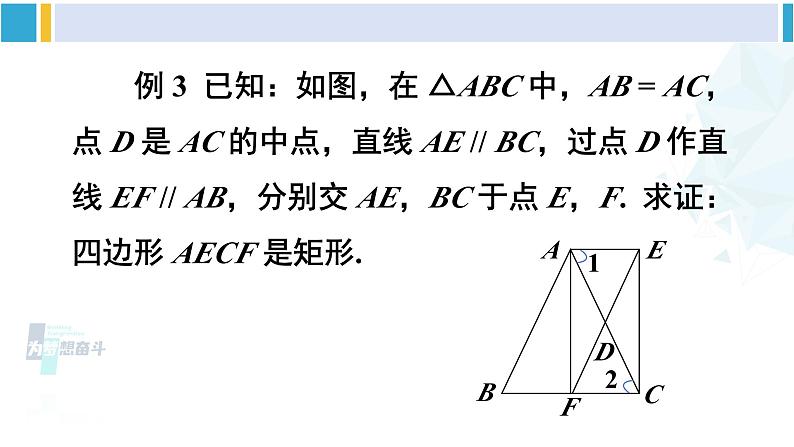
沪科版·八年级数学下册第 2 课时 矩形的判定新课导入1.矩形是轴对称图形,它有___条对称轴.2.矩形与一般平行四边形的区别与联系.2对边平行且相等对边平行且相等对角相等四个角都是直角互相平分相等且互相平分 工人师傅在做门窗或矩形零件时,要确保图形是矩形. 你有什么办法帮工人师傅测一测吗?推进新课 由矩形的定义可知,有一个角是直角的平行四边形是矩形. 除此之外,还有没有其他判定方法呢?例 2 如图,在 ABCD 中,对角线 AC = BD.求证: ABCD 为矩形.DABC证明 因为四边形ABCD是平行四边形,所以 AD = BC.又 ∵ DC = CD,AC = BD, ∴ △ADC ≌ △BCD. ∴ ∠ADC = ∠BCD.又∵ ∠ADC + ∠BCD = 180°, ∴ ∠ADC = ∠BCD = 90°.所以 ABCD为矩形.DABC 矩形的判定定理 1:对角线_____的平行四边形是矩形.相等 例 3 已知:如图,在 △ABC 中,AB = AC,点 D 是 AC 的中点,直线 AE // BC,过点 D 作直线 EF // AB,分别交 AE,BC 于点 E,F. 求证:四边形 AECF 是矩形.证明 ∵ AE // BC,∴ ∠1 = ∠2.在 △ADE 和 △CDF 中,∵ ∠1 =∠2,∠ADE =∠CDF,AD = CD,∴ △ADE ≌ △CDF.所以四边形 AECF 是平行四边形.又因为四边形 ABFE 是平行四边形,所以 EF = AB.∵ AC = AB,∴ EF = AC.所以四边形 AECF 是矩形.至少有几个角是直角的四边形是矩形?思 考 例 4 已知:如图,在四边形 ABCD 中,∠A =∠B = ∠C = 90°.求证:四边形 ABCD 是矩形.DABC证明 ∵ ∠A =∠B = ∠C = 90°,∴ ∠B + ∠C = 180°,∠A +∠B = 180°.∴ AB // CD,AD // BC.∴ 四边形 ABCD 是平行四边形.所以四边形 ABCD 是矩形. 矩形的判定定理 2:三个角是直角的_______是矩形.四边形随堂练习 1. 下列判定矩形的说法是否正确?为什么? (1)有一个角是直角的四边形是矩形. ( ) (2)四个角都相等的四边形是矩形. ( ) (3)对角线相等的四边形是矩形. ( ) (4)对角线互相平分,且有一个角是直角的四边形是矩形. ( )××√√2. 如图:(1)当_________时, ABCD 是矩形;(2)当_____________________________时,四边形 ABCD 是矩形.AC = BD ∠ABC = ∠BCD = ∠CDA = 90° 3. 已知平行四边形 ABCD 的对角线 AC,BD 交于点 O,△AOB 是等边三角形,AB = 4 cm.(1) 这个平行四边形是矩形吗?说明你的理由;(2) 求这个平行四边形的面积. 分析 首先根据△AOB是等边三角形及平行四边形对角线互相平分的性质判定出ABCD是矩形,再利用勾股定理计算边长,从而得到面积值.O解:(1)∵四边形 ABCD 是平行四边形,∵AO = AC,BO= BD.∵AO = BO,∴AC = BD.∴ ABCD 是矩形.(对角线相等的平行四边形是矩形)(2)在 Rt△ABC 中,∵ AB = 4 cm,AC = 2AO = 8 cm,∴ BC =S ABCD = AB·BC = 4× (cm).O (cm2). 4. 如图,将平行四边形 ABCD 的边 DC 延长至点 E,使 CE = DC,连接 AE,交 BC 于点 F.(1)求证:△ABF ≌ △ECF;(2)连接 AC、BE,则当∠AFC 与∠D 满足什么条件时,四边形 ABEC 是矩形?请说明理由.(1)证明:在平行四边形 ABCD 中,AB∥CD,AB = CD,∴∠BAE =∠AEC,又∵ CE = CD, ∴ AB = CE,在△ABF 和△ECF 中,∴ △ABF ≌ △ECF (AAS)(2)解:当∠AFC = 2∠D 时,四边形ABEC是矩形.∵ 四边形 ABCD 是平行四边形,∴ BC∥AD,∠BCE=∠D,由题意易得 AB∥EC,AB = EC,∴四边形 ABEC 是平行四边形.∵∠AFC =∠FEC +∠BCE,∴当∠AFC = 2∠D 时,则有∠FEC =∠FCE,∴FC = FE,∴四边形 ABEC 是矩形.对角线相等的平行四边形是矩形.有一个角是直角的平行四边形是矩形.有三个角是直角的四边形是矩形.矩形的判定方法:课后作业1.从教材习题中选取.2.完成练习册本课时的习题.
沪科版·八年级数学下册第 2 课时 矩形的判定新课导入1.矩形是轴对称图形,它有___条对称轴.2.矩形与一般平行四边形的区别与联系.2对边平行且相等对边平行且相等对角相等四个角都是直角互相平分相等且互相平分 工人师傅在做门窗或矩形零件时,要确保图形是矩形. 你有什么办法帮工人师傅测一测吗?推进新课 由矩形的定义可知,有一个角是直角的平行四边形是矩形. 除此之外,还有没有其他判定方法呢?例 2 如图,在 ABCD 中,对角线 AC = BD.求证: ABCD 为矩形.DABC证明 因为四边形ABCD是平行四边形,所以 AD = BC.又 ∵ DC = CD,AC = BD, ∴ △ADC ≌ △BCD. ∴ ∠ADC = ∠BCD.又∵ ∠ADC + ∠BCD = 180°, ∴ ∠ADC = ∠BCD = 90°.所以 ABCD为矩形.DABC 矩形的判定定理 1:对角线_____的平行四边形是矩形.相等 例 3 已知:如图,在 △ABC 中,AB = AC,点 D 是 AC 的中点,直线 AE // BC,过点 D 作直线 EF // AB,分别交 AE,BC 于点 E,F. 求证:四边形 AECF 是矩形.证明 ∵ AE // BC,∴ ∠1 = ∠2.在 △ADE 和 △CDF 中,∵ ∠1 =∠2,∠ADE =∠CDF,AD = CD,∴ △ADE ≌ △CDF.所以四边形 AECF 是平行四边形.又因为四边形 ABFE 是平行四边形,所以 EF = AB.∵ AC = AB,∴ EF = AC.所以四边形 AECF 是矩形.至少有几个角是直角的四边形是矩形?思 考 例 4 已知:如图,在四边形 ABCD 中,∠A =∠B = ∠C = 90°.求证:四边形 ABCD 是矩形.DABC证明 ∵ ∠A =∠B = ∠C = 90°,∴ ∠B + ∠C = 180°,∠A +∠B = 180°.∴ AB // CD,AD // BC.∴ 四边形 ABCD 是平行四边形.所以四边形 ABCD 是矩形. 矩形的判定定理 2:三个角是直角的_______是矩形.四边形随堂练习 1. 下列判定矩形的说法是否正确?为什么? (1)有一个角是直角的四边形是矩形. ( ) (2)四个角都相等的四边形是矩形. ( ) (3)对角线相等的四边形是矩形. ( ) (4)对角线互相平分,且有一个角是直角的四边形是矩形. ( )××√√2. 如图:(1)当_________时, ABCD 是矩形;(2)当_____________________________时,四边形 ABCD 是矩形.AC = BD ∠ABC = ∠BCD = ∠CDA = 90° 3. 已知平行四边形 ABCD 的对角线 AC,BD 交于点 O,△AOB 是等边三角形,AB = 4 cm.(1) 这个平行四边形是矩形吗?说明你的理由;(2) 求这个平行四边形的面积. 分析 首先根据△AOB是等边三角形及平行四边形对角线互相平分的性质判定出ABCD是矩形,再利用勾股定理计算边长,从而得到面积值.O解:(1)∵四边形 ABCD 是平行四边形,∵AO = AC,BO= BD.∵AO = BO,∴AC = BD.∴ ABCD 是矩形.(对角线相等的平行四边形是矩形)(2)在 Rt△ABC 中,∵ AB = 4 cm,AC = 2AO = 8 cm,∴ BC =S ABCD = AB·BC = 4× (cm).O (cm2). 4. 如图,将平行四边形 ABCD 的边 DC 延长至点 E,使 CE = DC,连接 AE,交 BC 于点 F.(1)求证:△ABF ≌ △ECF;(2)连接 AC、BE,则当∠AFC 与∠D 满足什么条件时,四边形 ABEC 是矩形?请说明理由.(1)证明:在平行四边形 ABCD 中,AB∥CD,AB = CD,∴∠BAE =∠AEC,又∵ CE = CD, ∴ AB = CE,在△ABF 和△ECF 中,∴ △ABF ≌ △ECF (AAS)(2)解:当∠AFC = 2∠D 时,四边形ABEC是矩形.∵ 四边形 ABCD 是平行四边形,∴ BC∥AD,∠BCE=∠D,由题意易得 AB∥EC,AB = EC,∴四边形 ABEC 是平行四边形.∵∠AFC =∠FEC +∠BCE,∴当∠AFC = 2∠D 时,则有∠FEC =∠FCE,∴FC = FE,∴四边形 ABEC 是矩形.对角线相等的平行四边形是矩形.有一个角是直角的平行四边形是矩形.有三个角是直角的四边形是矩形.矩形的判定方法:课后作业1.从教材习题中选取.2.完成练习册本课时的习题.
相关资料
更多










