





沪科版八年级下册第19章 四边形综合与测试教学课件ppt
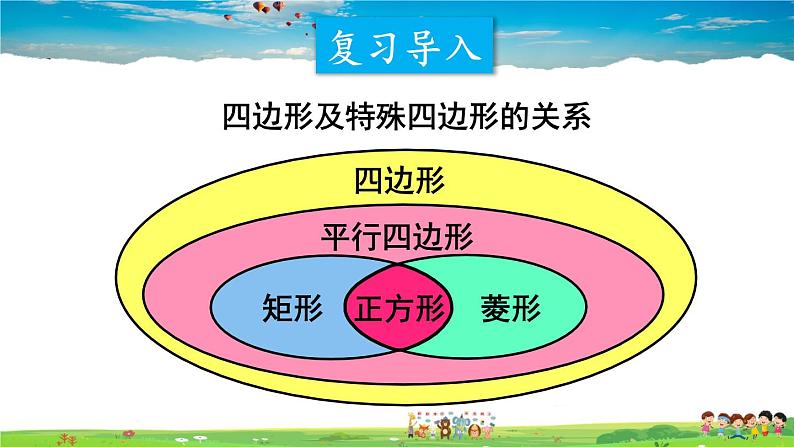
展开四边形及特殊四边形的关系
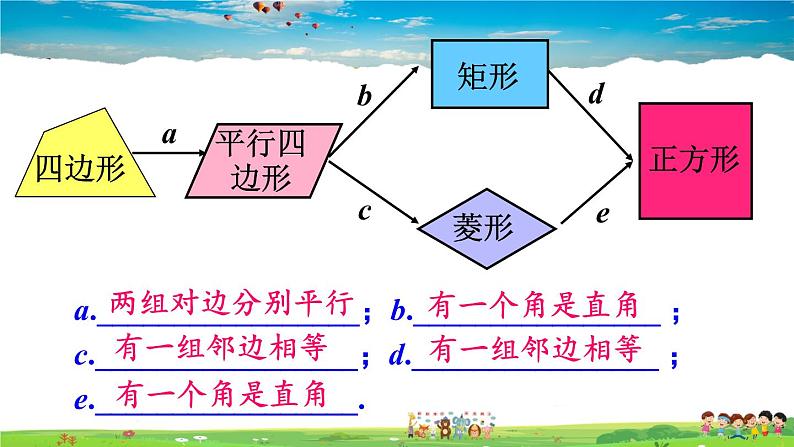
a._________________;b.________________ ;c._________________;d.________________ ;e._________________.
定义:________________的四边形是平行四边形.
性质1 平行四边形的对边_____.
性质2 平行四边形的对角_____.
性质3 平行四边形的对角线__________.
定理1 一组对边__________的四边形是平行四边形.
定理2 两组对边________的四边形是平行四边形.
定理3 对角线________的四边形是平行四边形.
(1)连接三角形两边中点的线段叫做三角形的中位线.
(2)定理:三角形两边中点的连线平行于第三边,并且等于第三边的一半.
①三角形有___条中位线.
②三角形的三条中位线把原三角形分成全等的 4 个小三角形.每个小三角形的周长为原三角形周长的____.每个小三角形的面积为原三角形面积的____.
(1)n 边形的内角和为___________ (n≥3).
(2)正多边形的每个内角都相等,都等于 _____________.
(3)多边形的外角和为360°,它与边数的多少无关.
定义:_______________的平行四边形是矩形.
性质1 矩形的四个角都是直角.
性质2 矩形的两条对角线相等.
推论 直角三角形斜边上的中线等于斜边的一半.
定理1 对角线相等的平行四边形是矩形.
定理2 三个角是直角的四边形是矩形.
定义:______________的平行四边形叫做菱形.
性质1 菱形的四条边都_______.
性质2 菱形的对角线_________.
定理1 四条边都相等的四边形是菱形.
定理2 对角线互相垂直的平行四边形是菱形.
定义:有一个角是_____,且有一组邻边____的平行四边形叫做正方形.
性质1 正方形的四条边都相等,四个角都是直角.
性质2 正方形的对角线相等且互相垂直平分.
有一组邻边相等的矩形是正方形.
有一个角为直角的菱形是正方形.
例 1 如图,E、F 是平行四边形 ABCD 对角线BD 上的两点,给出下列三个条件:①BE = DF; ②∠AEB =∠DFC;③AF∥ EC. 请你从中选择一个适当的条件____,使四边形 AECF 是平行四边形,并证明你的结论.
证明:如图,连接 AC 交 BD 于 O.∴AO = CO,OB = OD.又∵BE = DF,∴OB-BE = OD-DF,∴OE = OF. 又∵AO = CO,∴四边形 AECF 为平行四边形.
例 2 如图,点 E、F、G、H 分别为四边形ABCD 的边 AB、BC、CD、DA 的中点,试判断四边形 EFGH 的形状,并证明你的结论.
解:四边形 EFGH 为平行四边形.如图,连接 AC,在 △ACD 中,H、G 分别为AD、CD 的中点,∴HG∥AC,HG = AC,同理:EF∥AC,EF = AC,∴HG∥EF,HG = EF.∴四边形 EFGH 为平行四边形.
例 3 如图,四边形 ABCD 是菱形,对角线 AC = 8 cm,BD = 6 cm,DH⊥AB 于 H,求高 DH 的长.
解:∵四边形 ABCD 为菱形,∴AO = AC = 4 cm,AC⊥BD,∴在 Rt△AOB 中,
例 4 如图,正方形 ABCD 的对角线相交于点O,点 O 是正方形 A′B′C′O 的一个顶点,如果两个正方形的边长相等,那么正方形 A′B′C′O 绕点 O 无论怎样转动,两个正方形重叠部分的面积总等于一个正方形面积的四分之一,你能说明理由吗?
解:∵∠BOF+∠A′OB = 90°,∠A′OB+∠AOE = 90°.∴∠BOF =∠AOE. 又∵OA = OB,∠OAE = ∠OBF.∴△AOE ≌ △BOF.∴S△AOE = S△BOF .∴S四边形EBFO = S△BOF + S△OEB = S△AOE + S △OEB = S正方形ABCD.
例 5 如图,△ABC 中,BD,CE 为高,F 是边 BC 的中点,判断 △DEF 的形状,并说明理由.
解:△DEF 为等腰三角形.在 Rt△BEC 中,∵F 为 BC 的中点,∴EF = BC.同理:FD = BC.∴FD = EF,∴ △DEF 为等腰三角形.
例 6 如图,在 △ABC 中,点 O 是 AC 上的一动点,过点 O 作直线 MN∥ BC,设 MN 交∠BCA 的平分线于点 E,交∠BCA 的外角平分线于点 F.
(1)求证:OC = EF.
证明:∵CE为∠BCA 的平分线,∴∠BCE =∠ECO.又∵MN∥ BC,∠BCE =∠CEO.∴∠CEO =∠ECO,∴EO = OC.同理:OC = OF,∴OC = EF.
(2)当点 O 运动到何处时,四边形 AECF是矩形?并证明你的结论.
解:当点 O 运动到 AC 的中点时,四边形 AECF 是矩形. ∵由(1)可知,O 为 EF 的中点, 又∵O 为 AC 的中点. ∴四边形 AECF 为平行四边形. 又∵CE为∠BCA 的平分线, CF为∠ACD 的平分线,∠ECF = 90°. ∴四边形 AECF 是矩形.
1.下列图形:矩形、菱形、等腰梯形、正方形中对称轴最多的是( ) A. 矩形 B. 菱形 C. 等腰梯形 D. 正方形
2. 如图,平行四边形 ABCD 中,∠A 的平分线 AE 交 CD 于 E,AB = 5,BC = 3,则 EC 的长是( )
A. 1 B. 2C. 1.5 D. 3
3. 如图所示,直线 l 过正方形 ABCD 的顶点 B. A,C 两点到直线 l 的距离分别为 5 和 12,则正方形的边长是____.
4. 如图,在矩形 ABCD 中,AB = 3,AD = 4,点 P 在 AD 上,PE⊥AC 于 E,PF⊥BD 于 F,则 PE + PF =____.
初中华师大版第18章 平行四边形综合与测试优质教学复习课件ppt: 这是一份初中华师大版第18章 平行四边形综合与测试优质教学复习课件ppt,
2021学年第10章 相交线、平行线和平移综合与测试教学ppt课件: 这是一份2021学年第10章 相交线、平行线和平移综合与测试教学ppt课件,共31页。PPT课件主要包含了两条直线的位置关系,对顶角,点到直线的距离,平行线的性质,平行线的判定,平行线,平行公理及其推论,平行线的判定定理,平行线的性质定理,A是对顶角等内容,欢迎下载使用。
初中数学沪科版七年级下册第9章 分式综合与测试教学ppt课件: 这是一份初中数学沪科版七年级下册第9章 分式综合与测试教学ppt课件,共26页。PPT课件主要包含了知识回顾,未知数,最简公分母,分式方程,最简公,最简公分母不等于0,最简公分母等于0,例1解分式方程,或-1,归纳小结等内容,欢迎下载使用。













