湘教版八年级数学下册 第3章 图形与坐标第2课时 简单平移的坐标表示（课件）

这是一份湘教版八年级数学下册 第3章 图形与坐标第2课时 简单平移的坐标表示（课件），共24页。

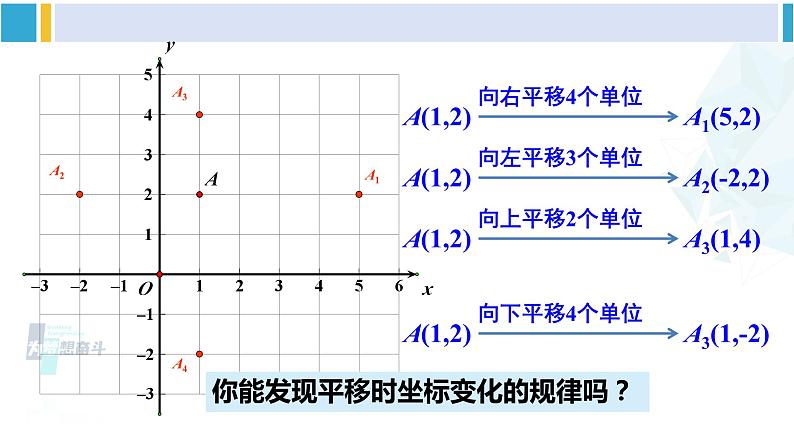
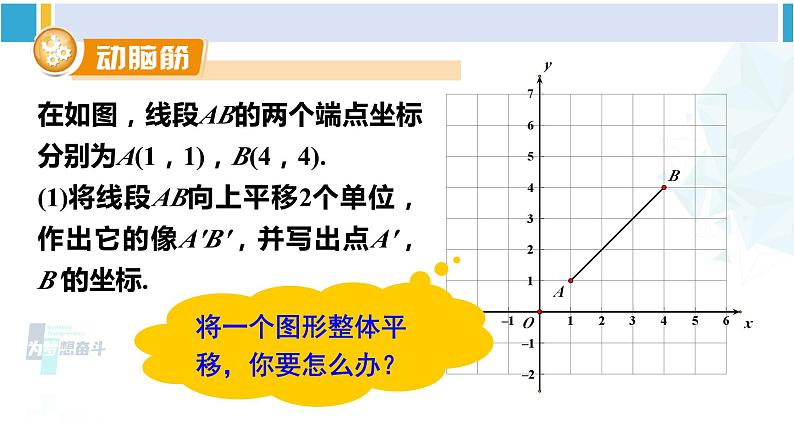
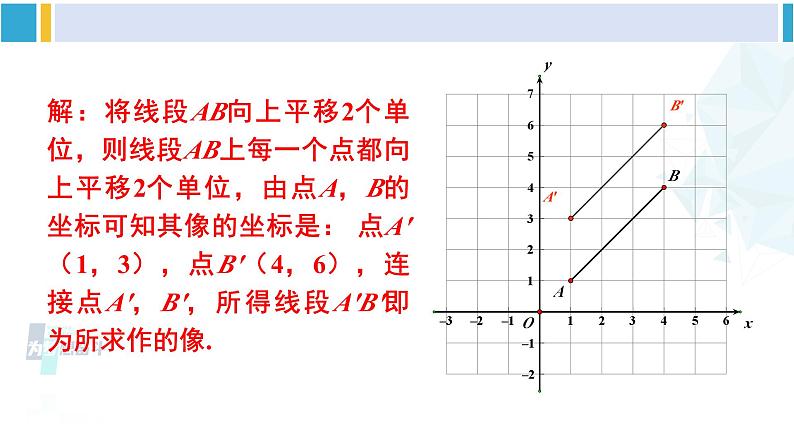
简单平移的坐标表示湘教·八年级下册复习回顾1.在平面直角坐标系中，关于x轴和y轴对称的点的坐标的特点：关于x轴对称的点横坐标相等，纵坐标互为相反数.关于y轴对称的点横坐标互为相反数，纵坐标相等.2.如何在平面直角坐标系中画一个关于x轴或y轴对称的图形. 先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形.探究新知 在平面直角坐标系中，A（1,2）分别沿坐标轴方向作以下变换，试作出A的像，并写出像的坐标.（1）点A向右平移4个单位，像为点A1;（2）点A向左平移3个单位，像为点A2;（3）点A向上平移2个单位，像为点A3;（4）点A向下平移4个单位，像为点A4.A(1,2)向右平移4个单位A1(5,2)A1A(1,2)向左平移3个单位A2(-2,2)A2A(1,2)向上平移2个单位A3(1,4)A3A(1,2)向下平移4个单位A3(1,-2)A4你能发现平移时坐标变化的规律吗？A(1,2)向右平移4个单位A1(5,2)A(1,2)向左平移3个单位A2(-2,2)A(1,2)向上平移2个单位A3(1,4)A(1,2)向下平移4个单位A3(1,-2)一般地，在平面直角坐标系中，将点（a,b）向右（或向左）平移k个单位，其像的坐标为（a+k,b）（或（a-k,b））；将点（a,b）向上（或向下）平移k个单位，其像的坐标为（a,b+k）（或（a,b-k））.总结归纳在如图，线段AB的两个端点坐标分别为A(1，1)，B(4，4).(1)将线段AB向上平移2个单位，作出它的像A′B′，并写出点A′，B′的坐标.将一个图形整体平移，你要怎么办？解：将线段AB向上平移2个单位，则线段AB上每一个点都向上平移2个单位，由点A，B的坐标可知其像的坐标是： 点A′（1，3），点B′（4，6），连接点A′，B′，所得线段A′B′即为所求作的像.A′B′A′B′(2)若点C(x, y)是平面内任一点，在上述平移下，像点C(x′, y′)与点C(x, y)的坐标有什么关系？C解：同理可求出，像点C′与点C之间的坐标关系为： 思考：在坐标系中，将一个点平移，你有什么窍门吗？上加下减“y”加减，右加左减“x”加减. 如图，△ABC的顶点坐标分别为A(3，3)，B(2，1)，C(5，1). （1）将△ABC向下平移5个单位，作出它的像，并写出像的顶点坐标.（2）将△ABC向左平移7个单位，作出它的像，并写出像的顶点坐标.【教材P98页】分析：根据平移的性质，将△ABC向下或向左平移k个单位，△ABC的每一个点都向下或向左平移了k个单位，求出顶点A，B，C的像的坐标，作出这些像点，依次连接它们，即可得到△ABC的像.A1B1C1解（1）将△ABC向下平移5个单位，则横坐标不变，纵坐标减5，由点A，B，C的坐标可知其像的坐标分别是A1（3，-2），B1（2，-4）， C1（5，-4），依次连接点A1，B1，C1，即可得△ABC的像△A1B1C1，如图.A1B1C1解（2）将△ABC向左平移7 个单位，则横坐标减7，纵坐标不变，由点A，B，C的坐标可知其像的坐标分别是A2（-4，3），B2（-5，1）， C2（-2，1），依次连接点A2， B2，C2，即可得△ABC的像△A2B2C2，如图.A2B2C2练习1. 填空.（1）点A(-1，2)向右平移2个单位，它的像是点A′_________；（2）点B(2，-2)向下平移3个单位，它的像是点B′_________.(1，2)(2，-5)【教材P99页】2.如图，线段AB的两个端点坐标分别为A（-2，-2），B（2，2）. 线段AB向下平移3个单位，它的像是线段A′B′.（1）试写出点A′， B′的坐标；A′B′A′(-2，-5)B′(2，-1)【教材P99页】（2）若点C（x，y）是平面内的任一点， 在上述平移下， 像点C′（x′，y′）与点C（x，y）的坐标之间有什么关系？A′B′解：由（1）可知，像点C′与点C之间的坐标关系为：3.如图，正方形ABCD的顶点坐标分别为A（2，2），B（2，-2），C（6，-2），D（6，2），将正方形ABCD向左平移4个单位，作出它的像，并写出像的顶点坐标.A′B′C′D′A′(-2，2)B′(-2，-2)C′(2，-2)D′(2，2)【教材P99页】随堂练习1.将点（2，1）向左平移2个单位长度得到点A′，则点A′的坐标是（ ）A.（2，3） B.（2，-1） C.（4，1） D.（0，1）2.在平面坐标系中，将点（-2，-3）向上平移3个单位，则平移后的点的坐标为_________.D（-2，0）3.将△ABC各顶点的横坐标不变，纵坐标分别加2，连接三个点所成的三角形是由△ABC（ ）A.向左平移2个单位所得B.向右平移2个单位所得C.向上平移2个单位所得D.向下平移2个单位所得C4.如图，三角形ABC三个顶点的坐标分别是：A（4，3），B（3，1），C（1，2）.（1）将三角形ABC三个顶点的横坐标都减去6，纵坐标不变，分别得到点A1，B1，C1，点A1，B1，C1坐标分别是什么？并画出相应的三角形A1B1C1；A1(-2，3)B1(-3，1)C1(-5，2)A1B1C1（2）三角形A1B1C1与三角形ABC的大小、形状和位置上有什么关系，为什么？A1B1C1解：△A1B1C1与△ABC的大小、形状完全相同，△A1B1C1是把△ABC向左平移了6个单位长度所得；A1B1C1（3）若三角形ABC三个顶点的横坐标都加5，纵坐标不变呢？解：若三角形ABC三个顶点的横坐标都加5，纵坐标不变，即△ABC向右平移了5个单位长度，所得三角形与原三角形的大小、形状完全相同. 课堂小结1.点平移的坐标特征.2.图形的平移方法及平移后顶点坐标的对应关系.