初中数学北师大版九年级上册2 矩形的性质与判定集体备课课件ppt

这是一份初中数学北师大版九年级上册2 矩形的性质与判定集体备课课件ppt，共32页。PPT课件主要包含了情景引入，导入新课，讲授新课，归纳总结，活动2，你能证明吗，形象图，证一证，典例精析，轴对称图形等内容，欢迎下载使用。

1.理解矩形的概念，知道矩形与平行四边形的区别与 联系.（重点）2.会证明矩形的性质，会用矩形的性质解决简单的问 题.（重点、难点）3.掌握直角三角形斜边中线的性质，并会简单的运用. （重点）
观察下面图形,长方形在生活中无处不在.
思考 长方形跟我们前面学习的平行四边形有什么关系？
你还能举出其他的例子吗？
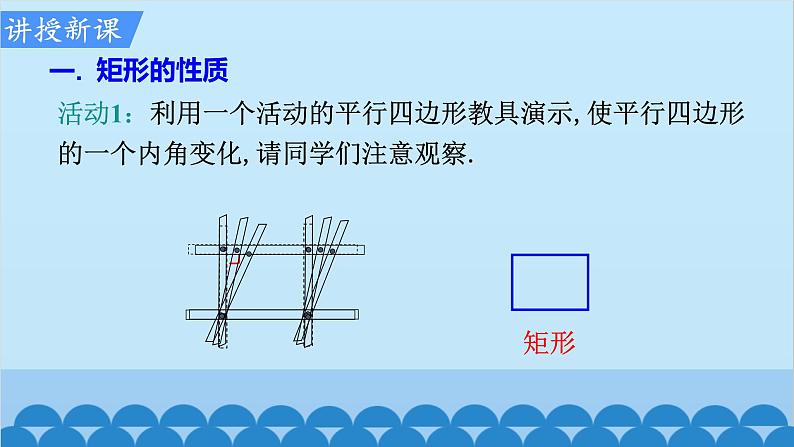
活动1：利用一个活动的平行四边形教具演示,使平行四边形的一个内角变化,请同学们注意观察.
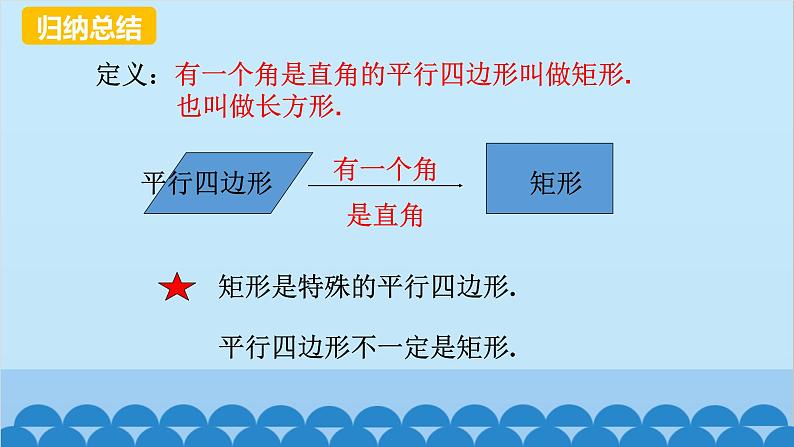
定义：有一个角是直角的平行四边形叫做矩形. 也叫做长方形.
平行四边形不一定是矩形.
思考 因为矩形是平行四边形，所以它具有平行四边形的所有性质，由于它有一个角为直角，它是否具有一般平行四边形不具有的一些特殊性质呢？
可以从边，角，对角线等方面来考虑.
准备素材：直尺、量角器、橡皮擦、课本、铅笔盒等.（1）请同学们以小组为单位,测量身边的矩形（如书本,课桌,铅笔盒等）的四条边长度、四个角度数和对角线的长度及夹角度数,并记录测量结果.
（2）根据测量的结果,你有什么猜想？
猜想1 矩形的四个角都是直角.
猜想2 矩形的对角线相等.
证明：∵四边形ABCD是矩形, ∴∠B=∠D,∠C=∠A, AB∥DC. ∴∠B+∠C=180°. 又∵∠B = 90°, ∴∠C = 90°. ∴∠B=∠C=∠D=∠A =90°.
如图,四边形ABCD是矩形,∠B=90°.求证： ∠B=∠C=∠D=∠A=90°.
证明：∵四边形ABCD是矩形,∴AB=DC,∠ABC=∠DCB=90°,在△ABC和△DCB中,∵AB=DC,∠ABC=∠DCB,BC= CB,∴△ABC≌△DCB.∴AC=DB.
如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相较于点O.求证：AC=DB.
矩形除了具有平行四边形所有性质，还具有的性质有：矩形的四个角都是直角.矩形的对角线相等.
几何语言描述：在矩形ABCD中，对角线AC与DB相交于点O.∠ABC=∠BCD=∠CDA=∠DAB =90°，AC=DB.
例1 如图,在矩形ABCD中,两条对角线AC,BD相交于点O,∠AOB=60°,AB=4 ,求矩形对角线的长.
解：∵四边形ABCD是矩形. ∴AC = BD， OA= OC= AC,OB = OD = BD ,∴OA = OB. 又∵∠AOB=60°, ∴△OAB是等边三角形， ∴OA=AB=4， ∴AC=BD=2OA=8.
矩形的对角线相等且互相平分
例2如图,在矩形ABCD中,E是BC上一点,AE=AD,DF⊥AE ,垂足为F.求证：DF=DC.
证明：连接DE.∵AD =AE,∴∠AED =∠ADE.∵四边形ABCD是矩形,∴AD∥BC,∠C=90°.∴∠ADE=∠DEC, ∴∠DEC=∠AED.又∵DF⊥AE, ∴∠DFE=∠C=90°.
又∵DE= DE,∴△DFE≌△DCE,∴DF=DC.
例3 如图，将矩形ABCD沿着直线BD折叠，使点C落在C′处，BC′交AD于点E，AD＝8，AB＝4，求△BED的面积．
解：∵四边形ABCD是矩形，∴AD∥BC，∠A＝90°，∴∠2＝∠3.又由折叠知∠1＝∠2，∴∠1＝∠3，∴BE＝DE.设BE＝DE＝x，则AE＝8－x.∵在Rt△ABE中，AB2＋AE2＝BE2，∴42＋(8－x)2＝x2，解得x＝5，即DE＝5.∴S△BED＝ DE·AB＝ ×5×4＝10.
矩形的折叠问题常与勾股定理结合考查
请同学们拿出准备好的矩形纸片,折一折,观察并思考.  （1）矩形是不是中心对称图形? 如果是,那么对称中心是什么？（2）矩形是不是轴对称图形?如果是,那么对称轴有几条?
矩形的性质（除中心对称外）对称性： .对称轴：.
1.如图，在矩形ABCD中，对角线AC，BD交于点O， 下列说法错误的是 （　　）A．AB∥DC B．AC=BD C．AC⊥BD D．OA=OB
2.如图，EF过矩形ABCD对角线的交点O，且分别交AB、CD于E、F，那么阴影部分的面积是矩形ABCD面积的_________.
　　　　　　　　　　　　　
3.如图，在矩形ABCD中，AE⊥BD于E，∠DAE：∠BAE＝3：1，求∠BAE和∠EAO的度数．
解：∵四边形ABCD是矩形，∴∠DAB＝90°，AO＝ AC，BO＝ BD，AC＝BD，∴∠BAE＋∠DAE＝90°，AO＝BO.又∵∠DAE：∠BAE＝3：1，∴∠BAE＝22.5°，∠DAE＝67.5°.∵AE⊥BD，∴∠ABE＝90°－∠BAE＝90°－22.5°＝67.5°，∴∠OAB＝∠ABE＝67.5°∴∠EAO＝67.5°－22.5°＝45°.
活动：如图，一张矩形纸片，画出两条对角线，沿着对角线AC剪去一半.
问题 Rt△ABC中，BO是一条怎样的线段？它的长度与斜边AC有什么关系？
猜想：直角三角形斜边上的中线等于斜边的一半.
证明: 延长BO至D, 使OD=BO, 连接AD、DC.
∵AO=OC, BO=OD，∴四边形ABCD是平行四边形.
∵∠ABC=90°,
∴平行四边形ABCD是矩形，
1. 直角三角形斜边上的中线等于斜边的一半.
例4 如图，在△ABC中，AD是高，E、F分别是AB、AC的中点．(1)若AB＝10，AC＝8，求四边形AEDF的周长；
解：∵AD是△ABC的高，E、F分别是AB、AC的中点，∴DE＝AE＝ AB＝ ×10＝5， DF＝AF＝ AC＝ ×8＝4，∴四边形AEDF的周长＝AE＋DE＋DF＋AF＝5＋5＋4＋4＝18；
(2)求证：EF垂直平分AD.
证明：∵DE＝AE，DF＝AF，∴E、F在线段AD的垂直平分线上， ∴EF垂直平分AD.
当已知条件含有线段的中点、直角三角形的条件时，可联想直角三角形斜边上的中线的性质进行求解．
例5 如图，已知BD，CE是△ABC不同边上的高，点G，F分别是BC，DE的中点，试说明GF⊥DE.
解：连接EG，DG. ∵BD，CE是△ABC的高， ∴∠BDC＝∠BEC＝90°. ∵点G是BC的中点，∴EG＝ BC，DG＝ BC. ∴EG＝DG. 又∵点F是DE的中点.∴GF⊥DE.
在直角三角形中，遇到斜边中点常作斜边中线，进而可将问题转化为等腰三角形的问题，然后利用等腰三角形“三线合一”的性质解题．
直角三角形斜边上的中线上的性质常见类型
如图，在△ABC中,∠ABC = 90°,BD是斜边AC上的中线.(1)若BD=3cm,则AC =_____cm;(2)若∠C = 30° ,AB = 5cm,则AC =_____cm, BD = _____cm.
1.矩形具有而一般平行四边形不具有的性质是 ( ) A.对角线相等 B.对边相等 C.对角相等 D.对角线互相平分 2.若直角三角形的两条直角边分别5和12,则斜边上的中线长为 ( ) A.13 B.6 C.6.5 D.不能确定 3.若矩形的一条对角线与一边的夹角为40°,则两条对角线相交的锐角是 ( ) A.20 ° B.40° C.80 ° D.10°
4.如图，在矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是AO、AD的中点，若AB=6cm，BC=8cm，则EF=____cm．
5.如图，△ABC中，E在AC上，且BE⊥AC．D为AB中点，若DE=5，AE=8，则BE的长为______．
6.如图,四边形ABCD是矩形,对角线AC,BD相交于点O,BE∥AC交DC的延长线于点E.（1）求证：BD=BE,（2）若∠DBC=30° , BO=4 ,求四边形ABED的面积.
(1)证明：∵四边形ABCD是矩形,∴AC= BD,AB∥CD.又∵BE∥AC,∴四边形ABEC是平行四边形,∴AC=BE,∴BD=BE.
(2)解：∵在矩形ABCD中,BO=4,∴BD = 2BO =2×4=8.∵∠DBC=30°,∴CD= BD= ×8=4,∴AB=CD=4,DE=CD+CE=CD+AB=8.在Rt△BCD中,BC=∴四边形ABED的面积= ×(4+8)× = .
7.如图，在矩形ABCD中，AB=6，AD=8，P是AD上的动点，PE⊥AC，PF⊥BD于F，求PE+PF的值.
解：连接OP.∵四边形ABCD是矩形，∴∠DAB=90°，OA=OD=OC=OB，∴S△AOD=S△DOC=S△AOB=S△BOC = S矩形ABCD= ×6×8=12.在Rt△BAD中，由勾股定理得BD=10，∴AO=OD=5，∵S△APO+S△DPO=S△AOD，∴ AO·PE+ DO·PF=12，即5PE+5PF=24，∴PE+PF= .