08，广东省深圳市南实集团麒麟中学2023-2024学年八年级下学期开学考试数学试题

这是一份08，广东省深圳市南实集团麒麟中学2023-2024学年八年级下学期开学考试数学试题，共26页。试卷主要包含了全卷共4页等内容，欢迎下载使用。

注意事项：
1．全卷共4页．
2．考试时间为90分钟，满分100分．
3．答题时，考生务必将姓名、班级、考号、考试科目、试卷类型用 铅笔填涂在答题卡上，并用黑色签字笔填写相应信息．请考生按要求在答题卷规定的位置上作答，在草稿纸、本试卷上答题一律无效．
第Ⅰ卷（选择题共30分）
一、选择题（10小题，每小题3分，共30分）
1. 下列二次根式是最简二次根式的是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】根据最简二次根式的概念判断．
【详解】解：A、，被开方数含分母，不是最简二次根式；
B、，被开方数含分母，不是最简二次根式；
C、，被开方数中含能开得尽方的因数，不是最简二次根式；
D、是最简二次根式；
故选：D．
【点睛】本题考查的是最简二次根式的概念，掌握被开方数不含分母、被开方数中不含能开得尽方的因数或因式的二次根式是最简二次根式是解题的关键．
2. 若，则下列不等式中，错误的是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】不等式的基本性质：（1）不等式两边加（或减）同一个数（或式子），不等号的方向不变；（2）您看到的资料都源自我们平台，家威杏 MXSJ663 免费下载不等式两边乘（或除以）同一个正数，不等号的方向不变；（3）不等式两边乘（或除以）同一个负数，不等号的方向改变．根据不等式的性质进行一一判断即可．
【详解】解：A、在不等式的两边同时乘以3，不等式仍成立，即，故本选项正确，不符合题意；
B、在不等式的两边同时除以，不等号方向改变，即，故本选项正确，不符合题意；
C、在不等式的两边同时先乘以4、再减去3，不等式仍成立，即，故本选项正确，不符合题意；
D、当时，该不等式不成立，故本选项错误，符合题意．
故选：D．
【点睛】主要考查了不等式基本性质，熟练掌握不等式的基本性质是解答此题的关键．
3. 不等式组 的解集在数轴上表示正确的是（ ）
A. B.
C. D.
【答案】C
【解析】
【详解】解①得 ；
解②得 ；
所以解集为： .
故选C.
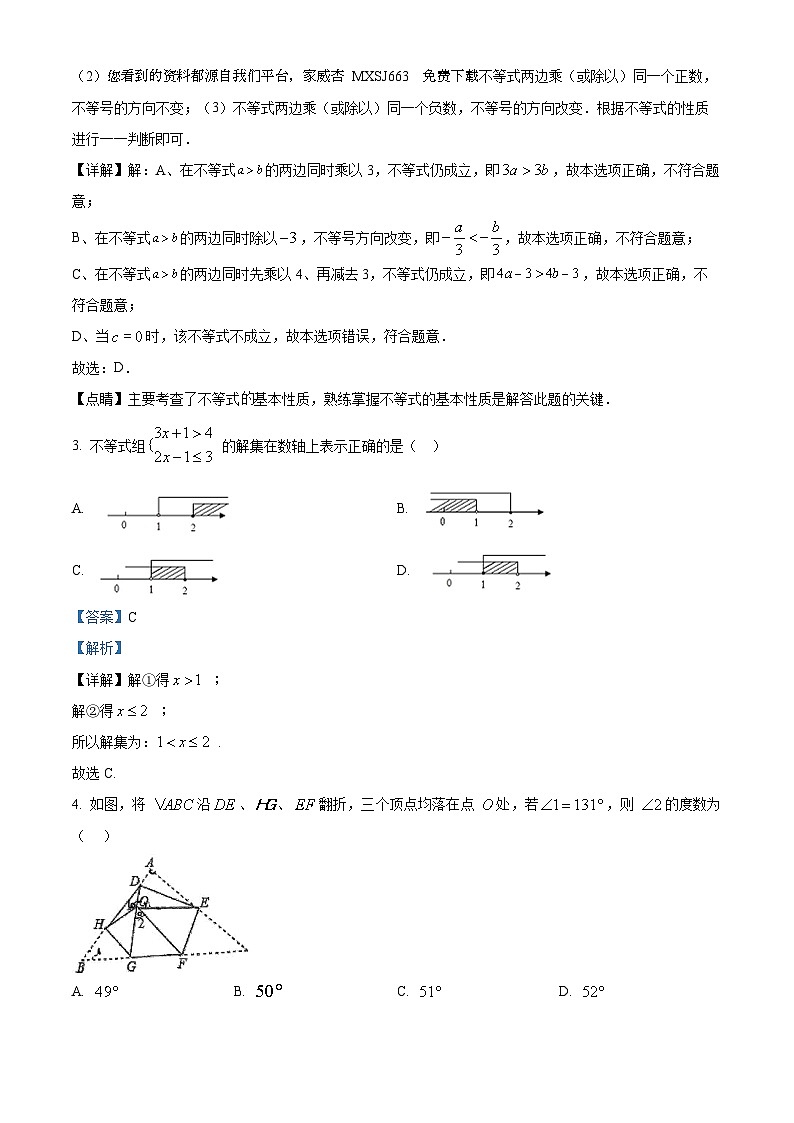
4. 如图，将 沿、、翻折，三个顶点均落在点 处，若，则 的度数为（ ）
A. B. C. D.
【答案】A
【解析】
【分析】本题考查轴对称的性质，以及三角形内角和，根据折叠的性质可得，，，又由题知，再利用三角形内角和进行等量代换，得到，最后结合，即可解题．
【详解】解：由折叠的性质可知，，，，
，
又，
即，
，即，
，
．
故选：A．
5. 给出下列命题：
①在直角三角形中，已知两边长为3和4，则第三边长为5；
②三角形的三边 满足，则；
③中，若，则 是直角三角形．
④中，若，则这个三角形是直角三角形． 其中，假命题的个数为（ ）
A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
【分析】本题考查对命题真假的判断，以及对勾股定理和勾股定理逆定理的辨析，根据勾股定理对①中边长进行分类讨论，即可判断①，利用勾股定理逆定理，即可判断②④，利用三角形内角和分别求出各角的度数，即可判断③．
【详解】解：①在直角三角形中，已知两边长为3和4，
若3和4均为直角边，则第三边长为5，
若3为直角边，4为斜边，则第三边长为，所以①错误，即①为假命题；
②三角形的三边 满足，则，所以②错误，即②为假命题；
③中，若，则，即是直角三角形，所以③正确，即③为真命题；
④中，若，设，，，
有，且，
则这个三角形不是直角三角形．所以④错误，即④为假命题；
综上所述，假命题的个数为3个，
故选：C．
6. 如图，是由7块颜色不同的正方形组成的长方形，已知中间小正方形的边长为1，这个长方形的面积为（ ）
A. 45B. 48C. 63D. 64
【答案】C
【解析】
【分析】由中央小正方形的边长为1厘米，设这7个正方形中最大的一个边长为x厘米，其余几个边长分别是x-1、x-2、x-3，根据长方形中几个正方形的排列情况，列方程求出最大正方形的边长，从而求得长方形长和宽，进而求出长方形的面积．
【详解】因为小正方形边长为1厘米，
设这7个正方形中最大的一个边长为x厘米，
因为图中最小正方形边长是1厘米，
所以其余的正方形边长分别为x−1，x−2，x−3，
3(x-3)-1=x
解得：x=5；
所以长方形的长为x+x−1=5+5-1=9，宽为x-1+x−2=5-1+5-2=7
长方形的面积为9×7=63(平方厘米)；
故选：C
【点睛】本题考查了对拼组图形面积的计算能力，利用了正方向的性质和长方形面积的计算公式．
7. 若直线和相交于点，则方程组的解为（ ）
A. B. C. D.
【答案】D
【解析】
【分析】求得直线和直线关于原点对称的直线，由题意得出点P的对应点，根据方程组的解和直线交点的关系即可求得．
【详解】解：直线和关于原点对称的直线为y=mx+3和，
∵直线和相交于点P（2，3），
∴直线y=mx+3和y=2xn相交于点（2，3），
∴方程组的解为；
故选：D．
【点睛】本题考查了对一次函数与二元一次方程组的关系的理解和运用，题目比较典型，求得直线关于原点的对称直线是解题的关键．
8. 如图，已知在中，，从直角三角形两个锐角顶点所引的中线的长，，则斜边的长为（ ）
A. B. C. D.
【答案】A
【解析】
【分析】本题考查勾股定理，以及三角形中线的性质，设，，在与中，利用勾股定理建立方程，联立方程得出，即可求得斜边的长．
【详解】解：设，，
由题知，，
，，，
，即①，
且有，即②，
根据①②整理得，，即，
则斜边的长为．
故选：A．
9. 如图，一大楼的外墙面与地面垂直，点P在墙面上，若米，点P到的距离是8米，有一只蚂蚁要从点P爬到点B，它的最短行程是（ ）米．
A. B. C. D.
【答案】D
【解析】
【分析】可将教室的墙面与地面展开，连接，根据两点之间线段最短，利用勾股定理求解即可．
【详解】解：如图，过P作于G，连接，
（米），（米），
（米），
（米），
（米）
这只蚂蚁的最短行程应该是米，
故选：D．
【点睛】本题主要考查了平面展开-最短路径问题，解题关键是立体图形中最短距离，通常要转换为平面图形的两点间的线段长来进行解决．
10. 如图，中，交 于 ，平分 交 于 ，为 的延长线上一点，交 的延长线于 ，的延长线交 于 ，连接，下列结论：①，②，③，④其中正确的结论有（ ）个．
A. 1B. 2C. 3D. 4
【答案】D
【解析】
【分析】本题考查了三角形的内角和定理，三角形外角的性质，以及角平分线的性质，根据三角形内角和即可判断①，根据角平分线性质得到，由三角形内角和可得，再对其进行变形，即可判断②，根据角平分线性质和三角形面积公式，即可判断③，根据三角形的内角和定理，以及三角形外角的性质，即可判断④．
【详解】解：记于点，如图所示：
，，
，
，
，即①正确；
平分 交 于 ，
，
，
即②正确；
平分 交 于 ，
点到，的距离相等，
，
即③正确；
，，
，
，
，
，
即④正确；
综上所述，正确的有①②③④共4个，
故选：D．
第Ⅱ卷（非选择题共70分）
二、填空题（5小题，每小题3分，共15分）
11. 因式分解： _____．
【答案】
【解析】
【分析】先提公因式，再运用完全平方公式分解因式．
【详解】解：原式
，
故答案为：．
【点睛】本题考查因式分解．熟记乘法公式，熟练掌握因式分解的方法，是解题的关键．
12. 如图，把一个矩形纸片 放入平面直角坐标系中，使、分别落在 轴、轴上，连接 ，将纸片 沿 折叠，使点 落在的位置上． 若，，则点的坐标为_________________．
【答案】
【解析】
【分析】本题过点作于点，交于点，由矩形的性质和折叠的性质，证明，得到，设，则，在中应用勾股定理构建方程，即可求出和，使用等面积法求出，点的纵坐标就求出来了，最后再解，求出，即点的横坐标．即可解题．
【详解】解：过点作于点，交于点，如图所示：
四边形为矩形，，，
，，，
由题易知，四边形为矩形，
有，
由折叠的性质可知，，，，
，
，
，
设，则，
有， 即，解得，
，
，解得，
，，
，
点的坐标为，
故答案为：．
【点睛】本题考查矩形的性质，全等三角形的性质和判定，折叠的性质，勾股定理，熟练掌握相关性质并灵活运用，即可解题．
13. 一组数据的方差计算公式为，则这组数据的方差是_____________．
【答案】
【解析】
【分析】本题主要考查方差．根据题意可得平均数，再根据方差的定义可得答案．
【详解】解：平均数为：，
故方差是：．
故答案为：．
14. 如图，在中，，，点D在的边上，连接，若为等腰三角形，则该等腰三角形的顶角的度数为______．
【答案】或或
【解析】
【分析】由，，可得，再分两种情况讨论：①当在上时，②当在上时，从而可得答案．
【详解】解：∵，，
∴，
∵为等腰三角形，
①当在上时，
当时，
∴，
∴顶角，
当时，
此时顶角，
当时，
∴，
此时顶角．
②当在上时，
∴，
此时顶角，
综上：顶角为或或．
【点睛】本题考查的是三角形的内角和定理的应用，等腰三角形的性质，清晰的分类讨论是解本题的关键．
15. 如图，在平面直角坐标系中，点M(6，0)，N(0，6)，一点P从点O出发，以每秒1个单位长度的速度沿折线O-N-M运动. 设点P运动时间为t，当时，直线上有一个动点C和y轴上有一个动点D，则PD＋DC＋OC的最小值是_____.
【答案】
【解析】
【分析】先根据当时，ON+NP=，NP=5，PM=，求得点P的坐标为（5，1），再作点P关于y轴对称的点P'，作点O关于直线x=的对称点O'，则P'（-5，1），O'（1，0），连接O'P'，交y轴于点D，交直线x=于点C，则此时PD+DC+OC值最小，等于线段O'P'的长，然后运用勾股定理求解即可.
【详解】∵ON=6，
∴当t=6+5时，ON+NP=6+5，NP=5，PM=，
作PH⊥x轴与点H，则△MPH是等腰直角三角形,
∵PM=，
∴PH=HM=1,
∴OH=5,
∴P(5,1),
作点P关于y轴对称的点P'，作点O关于直线x=的对称点O'，则P'（-5，1），O'（1，0），
连接O'P'，交y轴于点D，交直线x=于点C，则此时PD+DC+OC值最小，等于线段O'P'的长.
∵P'（-5，1），O'（1，0），
∴PD+DC+OC=O'P'=，
∴PD+DC+OC最小值为.
故答案为.
【点睛】本题属于几何变换综合题，主要考查了轴对称最短，等腰直角三角形的判定与性质，及勾股定理的综合应用，正确作出辅助线是解答本题的关键．
三、解答题（本大题有7题，其中16题12分，17题6分，18题6分，19题6分，20题8分，21题9分，22题8分，共55分）
16. 计算．
（1）
（2）；
（3）；
（4）．
【答案】（1）；
（2）；
（3）；
（4）．
【解析】
【分析】（1）本题考查实数的混合运算，掌握实数的混合运算法则，即可解题．
（2）本题考查实数的混合运算，掌握实数的混合运算法则，即可解题．
（3）本题考查解二元一次方程组，掌握加减消元法或代入消元法，即可解题．
（4）本题考查解二元一次方程组，掌握加减消元法或代入消元法，即可解题．
【小问1详解】
解：
；
【小问2详解】
解：
；
【小问3详解】
解： ，
由得：，
由得：，解得，
将代入①中，有，解得，
方程组的解为；
【小问4详解】
解：
由①得：，即③，
由②得：④，
由③④得：，解得，
将代入②中得：，解得，
方程组的解为．
17. 解不等式组：，并写出该不等式组的整数解．
【答案】不等式的解集为，整数解为，，，0
【解析】
【分析】先求出两个一元一次不等式的解集，然后求出不等式组的解集，最后找出其中的整数即可
【详解】解：
解不等式①：，解得，
解不等式②：，得，解得
∴不等式的解集为，
∴不等式组的整数解为，，，0．
【点睛】本题考查了一元一次不等式组的解法，熟练掌握一元一次不等式组的解法是解答本题的关键．先分别解两个不等式，求出它们的解集，再求两个不等式解集的公共部分．不等式组解集的确定方法是：同大取大，同小取小，大小小大取中间，大大小小无解．
18. 某中学对本校学生每天完成作业所用时间的情况进行了抽样调查．随机调查了九年级部分学生每天完成作业所用的时间，并根据统计结果制成了条形统计图（时间取整数，图中从左至右依次为第1、2、3、4、5组）和扇形统计图，请结合图中信息回答下列问题：
（1）本次调查的学生人数为 ；
（2）补全条形统计图；
（3）根据图中提供的信息，可知下列结论正确的是 （只填所有正确的代号）；
A.由图（1）知，学生完成作业所用时间的中位数在第三组内
B.由图（1）知学生完成作业所用时间的众数在第二组内
C.图中，90～120时间段对应的扇形圆心角为108°
（4）学生每天完成作业时间不超过120分钟，视为课业负担适中，根据以上调查，估计该校九年级560名学生中，课业负担适中的学生有多少人？
【答案】（1）60；（2）见解析；（3）A、C；（4）336人
【解析】
【分析】（1）根据第1组的人数和所占的百分比即可得出总人数；
（2）用总人数减去其它时间段的人数，求出第二组的人数，从而补全统计图；
（3）根据中位数、众数以及圆心角的求法分别对每一项进行分析，即可得出答案；
（4）用总人数乘以时间不超过120分钟的人数所占的百分比即可．
【详解】解：（1）本次调查的学生人数为：6÷10%＝60（人），
故答案为：60；
（2）60～90时间段的人数有：60×20%＝12（人），补全统计图如下：
（3）A、∵共有60人，处于中间位置的是第30、31个数的平均数，
∴学生完成作业所用时间的中位数在第三组内；
B、∵第三组的人数最多，有18人，
∴学生完成作业所用时间的众数在第三组内；
C、90～120时间段对应的扇形圆心角为360°×＝108°；
正确的是A、C；
故答案为：A、C；
（4）根据题意得：
560×＝336（人），
答：课业负担适中的学生有336人．
【点睛】此题主要考查统计调查的应用，解题的关键是根据题意找到数量关系列式求解．
19. 在平面直角坐标系 中，对于、两点给出如下定义：若点 到 、轴的距离中的最大值等于点 到、轴的距离中的最大值，则称、两点为“等距点”，如图1中的、两点即为“等距点”．
（1）已知点的坐标为 ．
①在点 ，，中，点的“等距点”是 ；
②若与点不重合的点在直线 上，且 、两点为“等距点”，则点 的坐标为 ；
（2）直线与 轴交于点 ，与 轴交于点 ． 若 ，是直线 上的两点，且 、为“等距点”，求 的值．
【答案】（1）①，；②；
（2）的值为或．
【解析】
【分析】本题考查了平面直角坐标系中点到、轴的距离，一元一次方程的应用，以及对题干“等距点”定义的理解．
（1）①根据“等距点”定义即可解题．
②设点的坐标为，，根据“等距点”定义，建立等式、，，分别讨论所得的值是否符合题意，即可解题．
（2）由题意得到，，根据“等距点”定义，建立等式，再分别讨论所得的值是否符合题意，即可解题．
【小问1详解】
解：①点的坐标为
点到 、轴的距离中的最大值为，
到 、轴的距离中的最大值为，
到 、轴的距离中的最大值为，
到 、轴的距离中的最大值为，
点的“等距点”是，，
故答案为：，．
②与点不重合的点在直线 上，
设点的坐标为，，
、两点为“等距点”，
，解得，
，解得（不合题意，舍去），
，则（不合题意，舍去），
综上所述，点的坐标为，
故答案为：．
【小问2详解】
解：，是直线 上的两点，
，，
、为“等距点”，
①，解得（不合题意，舍去），
，解得，
②，解得（不合题意，舍去），
，解得，
综上所述，的值为或．
20. 张氏包装厂承接了一批纸盒加工任务，用如图①所示的长方形和正方形纸板作侧面和底面，做成如图②所示的竖式与横式两种上面无盖的长方体纸盒（加工时接缝材料不计）．
（1）做1个竖式纸盒和2个横式纸盒，需正方形纸板___________张（直接填空），需长方形纸板___________张（直接填空）．
（2）若该厂购进正方形纸板162张，长方形纸板338张，问竖式纸盒、横式纸盒各加工多少个，恰好能将购进的纸板全部用完？（要求列二元一次方程组解决此问题）
【答案】（1）5；10
（2）制作竖式纸盒38个、横式纸盒62个，恰好能将购进的纸板全部用完
【解析】
【分析】（1）根据1个竖式纸盒需要长方形纸板4张，正方形纸板1张，1个横式纸盒需要长方形纸板3张，正方形纸板2张，求出做1个竖式纸盒和2个横式纸盒需要的正方形纸板和长方形纸片的张数即可；
（2）设制作竖式纸盒x个、横式纸盒y个，根据制作竖式纸盒和横式纸盒需要的正方形和长方形纸板数列出方程组，解方程即可．
【小问1详解】
解：需正方形纸板：（张），
长方形纸板：（张），
故答案为：5；10．
【小问2详解】
解：设制作竖式纸盒x个、横式纸盒y个，根据题意得：
，
解得：，
答：制作竖式纸盒38个、横式纸盒62个，恰好能将购进的纸板全部用完．
【点睛】本题主要考查了二元一次方程组的应用，解题的关键是根据正方形和长方形张数列出方程组．
21. 点在射线上，点、为射线上两个动点，满足，，平分．
（1）如图，当点在右侧时，求证：；
（2）如图，当点在左侧时，求证：；
（3）如图，在（2）的条件下，为延长线上一点，平分，交于点，平分，交于点，连接，若，，则的度数是多少．
【答案】（1）见解析 （2）见解析
（3）60度
【解析】
【分析】本题主要考查了平行线的判定与性质，角平分线的定义；
（1）通过证明，利用同位角相等，两直线平行即可得出结论；
（2）过点作，交于点，利用（1）的结论和平行线的性质即可得出结论；
（3）设，则，，；利用已知条件用含的式子表示，，，，再利用，得到关于的方程，解方程求得的值，则，结论可求．
【小问1详解】
平分，
，
又，
，
∴，
，
，
，
∴；
【小问2详解】
过点作，交于点，如图，
由（1）同理可证：，
，
，，
，
；
【小问3详解】
设，
则，，
，
平分，
，
，
，
，
，
，
，
，
，
，
解得：，
．
22. 如图1，直线与x轴交于点A，与y轴交于点C，经过点C的直线（m，n为常数）与x轴交于点B，且．
（1）点A坐标为______；直线的函数表达式为______；
（2）点P是直线上一动点，
①如图1，当点P在第二象限时，过点P作轴于点D，交直线与点E，当时，点P坐标为______；
②当时，点P的坐标为______；
（3）如图2，在平面内有一点，连接CM交x轴于点N，连接AM，在平面内存在点Q，使得，且，请直接写出点Q的坐标为______．
【答案】（1）；
（2）①；②或
（3）或
【解析】
【分析】（1）把代入求出点A的坐标即可；求出点C，点B坐标，代入解析式可求解；
（2）①设点P的横坐标为t，则，，，根据，列出关于t的方程，解方程即可得出结果；
②先求出的面积，由三角形的面积公式可求解即可；
（3）先求出，由“”可证，可得，，即可求解．
【小问1详解】
解：把代入得：，
解得：，
∴点A的坐标为，
把代入得：，
∴点C的坐标为：，
∴，，
∵，
∴，
∴点，
∴，
解得：，
∴直线的函数表达式为；
故答案为：；．
【小问2详解】
解：①设点P的横坐标为t，则，，，
∴，，
∵，
∴，
解得：，
∴点P的坐标为；
故答案为：；
②∵点，点，点，
∴，，
∴，
∴，
∵点P是直线上一动点，
∴设点，
∴，
∴，
∴点或；
故答案为：或．
【小问3详解】
解：如图，延长交y轴于H，
设直线的解析式为，
把点，点代入得：，
解得：，
∴直线的解析式为，
当时，，
∴点，
∴，
又∵，，
∴，
∴，
∵
∴设直线的解析式为
把点代入得，
解得：，
∴直线的解析式为，
当时，，
∴点，
∴，
∴，
∴，
如图，当点Q在的上方时，连接，
∵，
∴，
∴，
∴，
∴，
又∵，，
∴，
∴，，
∴点，
当点在的下方时，
∵，
∴点A是的中点，
∴；
综上所述：点Q坐标或．
故答案为：或．
【点睛】本题是一次函数综合题，考查了待定系数法求解析式，一次函数的性质，三角形的面积公式，全等三角形的判定和性质等，等腰三角形的性质，中点坐标公式，求出是解题的关键．