青岛数学七年级下册 13.4 综合与实践 PPT课件

这是一份青岛数学七年级下册 13.4 综合与实践 PPT课件，共38页。
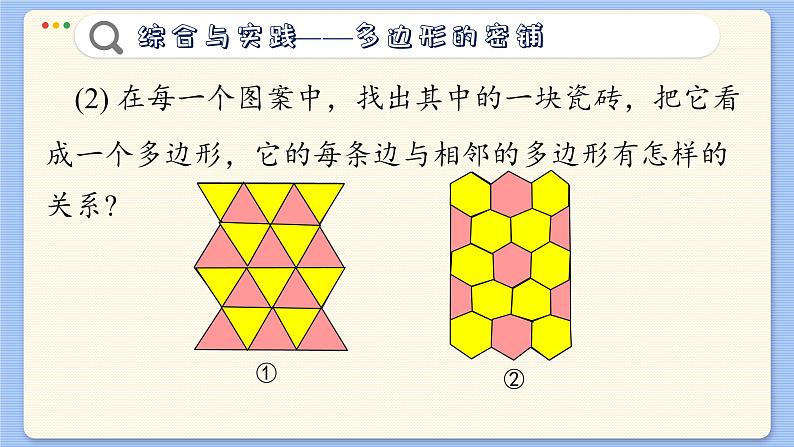
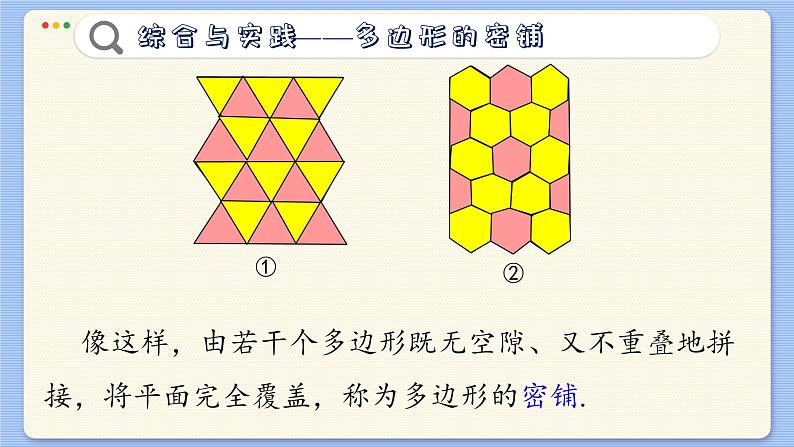
第13章 平面图形的认识青岛版 七年级下册综合与实践—多边形的密铺 图1是用瓷砖拼铺的房屋外墙面或地面的图样.你见过类似的图案吗? 观察图1中的两个图案，思考下面的问题：(1) 这些图案分别是用什么形状的瓷砖拼成的? (2) 在每一个图案中，找出其中的一块瓷砖，把它看成一个多边形，它的每条边与相邻的多边形有怎样的关系? 像这样，由若干个多边形既无空隙、又不重叠地拼接，将平面完全覆盖，称为多边形的密铺. (3) 在每一个图案中，分别找出一个多边形的顶点，它还是周围哪几个多边形的顶点?两人一组，完成下面的活动： (1) 用硬纸板分别剪出边长都是3 厘米的正三角形、正方形、正五边形正六边形纸板各若干个. (2) 仿照图1给出的图样，用你剪出的正三角形和正六边形纸板分别进行密铺. (3) 能只用正方形纸板进行密铺吗? (4) 分别观察你拼成的密铺图案，你发现以一个多边形的顶点为公共顶点的各个角的和是多少度? 密铺时，多边形的每条边都是该多边形与相邻多边形的公共边，每个顶点处各内角之和是360°. (5) 只用正五边形纸板密铺吗?试一试. (6) 用同样大小的正多边形拼接时，为什么单独用正三角形、正方形或正六边形都可以进行密铺，而单独用正五边形却不能密铺? 用多边形拼接图案，只有当以任何一个公共顶点为顶点的各个角恰好能拼成一个周角时，才有可能做到既无空隙又不重叠. 用同一种正多边形拼接图案时，由于正三角形、正方形、正六边形的每个角依次是 60°，90°和120°，所以在这些多边形的任何一个顶点处，分别用6个正三角形、4个正方形或3个正六边形的角都可以拼成一个周角. 正五边形的每个角是108°，而108不能整除360. 如果用3个正五边形拼接，必有两个正五边形之间留有空隙；如果用4个正五边形拼接，必有两个角的一部分相互重叠.因此单独用正五边形不能密铺. (7) 除了上述三种正多边形外，还有没有其他的正多边形，只用同样大小的这种正多边形就可以进行密铺? 当n＞6时，正n边形的每个角大于120°，小于180°，其度数不能整除360所以只用一种这样的正多边形不能密铺. 只用一种形状和大小都相同的任意四边形能进行密铺吗? (1) 我们知道，用大小相同的正方形可以密铺，用形状和大小都相同的长方形可以密铺吗?用形状和大小都相同的平行四边形呢?画一画，试一试. (2) 如图是只用一种形状和大小都相同的四边形密铺而成的图案. 只用一种形状和大小都相同的任意四边形都能密铺吗?用硬纸片任意裁出形状和大小都相同的四边形若干个，试一试. 这时，除考虑在公共顶点处要拼成一个周角外，还应当注意些什么?由此你能得出什么结论? 因为四边形的内角和等于360°，并且在拼接时，可以将两个四边形相等的两条边作为公共边，所以任意四边形都可以密铺. (3) 如图是一个画在方格纸上的四边形，你会只用这种四边形进行密铺吗?试试看. 用硬纸片剪一个图形所示的四边形作为模板，在方格纸上画出你的设计，并与同学交流. (4) 用硬纸片剪出若干个形状和大小都相同的任意三角形，用这样的纸片能进行密铺吗?为什么? 先用两个三角形中任意两条相等的边作为公共边，拼成一个四边形. 因为用形状和大小都相同的四边形能密铺，所以用形状和大小都相同的三角形也能密铺. (1) 观察图6和图1，这两种密铺方式有什么不同和相同? 每个图案是由哪几种正多边形密铺而成的? 在图6的每个图案中，各个正多边形的边长有什么关系? 图6①②③都是用正三角形和正方形这两种多边形密铺的，你能说出这三种密铺方式有什么不同吗?你能用这两种正多边形设计出其他的密铺图案吗?试一试. (2) 我们知道，只用正八边形不能密铺.如果用边长相等的正八边形和正方形，能密铺吗? (3) 观察图7和图8. 它们是同一种密铺图案吗?为什么? (4) 观察图9中的几个图案，它们分别是由哪几种正多边形密铺而成的?①②③④ 请你用同样的正三角形和与正三角形边长相等的正六边形设计密铺图案，与同学交流. (5) 再设计几个用不同的正多边形密铺的图案，并在全班展示. (6) 你能围绕正多边形的密铺问题，作进一步的探索吗?就你的研究过程和结果写成一篇小论文，并在班内交流. 课外活动时间，学校足球场热火朝天. 七年级的同学们聚在一起，热烈地谈论着刚才的足球比赛.小莹忽然想起：“这黑白相间的足球真吸引人，它的黑块和白块各有多少呢?” 大家围着一个足球仔细地观察，发现黑块是球面正五边形，白块是球面正六边形.大家好不容易查清了黑块共 12 块(图10)，白块的个数就不容易数清了. 一会儿，小亮先想出了一个办法: 在白块上分别贴上带有1，2，3，···的标签，就容易查清了! 很快地，小莹也想出了另一个解决的方法：设有n个白块图10 足 球正六边形，因为每个白块正六边形都有3 条边是它与黑块正五边形的公共边，足球上所有这样的公共边共有3n条.而12个黑块正五边形共有60条边，于是3n＝60，解得n＝20，所以白块正六边形共有 20个. 小莹的结论对吗?习题 12.4 1. 只用一种正多边形密铺时，如果每个顶点处有3 个这种正多边形相拼接，那么这种正多边形是正几边形?∵这种正多边形的内角是360°÷3＝120°∴这种正多边形是正六边形 2. 请分别用如图所示的三种梯形纸片进行密铺，与同学交流.(密铺方法不确定)给出两种密铺图形 3. 我们知道，只用同样大小的正五边形不能密铺.那么，正五边形与其他正多边形组合有密铺的可能吗?用同样大小的正五边形与同样大小的顶角为36°的等腰三角形组合能进行密铺吗?如果你认为可能密铺，请画出图形；如果你认为不可能密铺，请说明原因.略本课结束！