高中物理第六章 圆周运动4 生活中的圆周运动导学案

这是一份高中物理第六章 圆周运动4 生活中的圆周运动导学案，共12页。

1.会分析火车转弯、汽车过拱形桥等实际运动问题中向心力的来源(重点)。
2.能解决生活中的圆周运动问题(重难点)。
3.了解航天器中的失重现象及其原因。
4.了解离心运动及物体做离心运动的条件，知道离心运动的应用及危害。
一、火车转弯
图甲为摩托车在水平道路上转弯，图乙为火车转弯，图丙为火车轮缘与铁轨，摩托车和火车转弯向心力来源相同吗？铁路弯道处铁轨内外高度相同吗？为什么要这样设计？
________________________________________________________________________
________________________________________________________________________
1.铁路弯道的特点
铁路弯道处，外轨高于内轨，若火车按规定的速度v0行驶，转弯所需的向心力完全由重力和支持力的合力提供，即mgtan θ＝meq \f(v02,R)，如图所示，则v0＝________，其中R为弯道半径，θ为轨道平面与水平面间的夹角(θ很小的情况下，tan θ≈sin θ)。
2．汽车转弯特点
(1)水平弯道：由____________提供向心力，汽车速度最大时，μmg＝eq \f(mvm2,R)，可得vm＝________。
(2)增大汽车安全转弯速度的有效方法
①________转弯半径。
②把转弯处设计成____________(填“外高内低”或“外低内高”)路面(类似火车转弯)。
若v0为火车不受轨道侧压力的临界速度，当火车不按规定速度行驶时，对铁轨有什么影响？
________________________________________________________________________
例1 如图所示，在修筑铁路时，弯道处的外轨会略高于内轨。当火车以规定的行驶速度转弯时，内、外轨均不会受到轮缘的挤压，设此时火车的速度大小为v，重力加速度为g，两轨所在平面的倾角为θ，则下列说法不正确的是( )
A．该弯道的半径r＝eq \f(v2,gtan θ)
B．当火车质量改变时，规定的行驶速度大小不变
C．当火车速率大于v时，内轨将受到轮缘的挤压
D．当火车以规定的行驶速度转弯时，向心加速度大小为an＝gtan θ
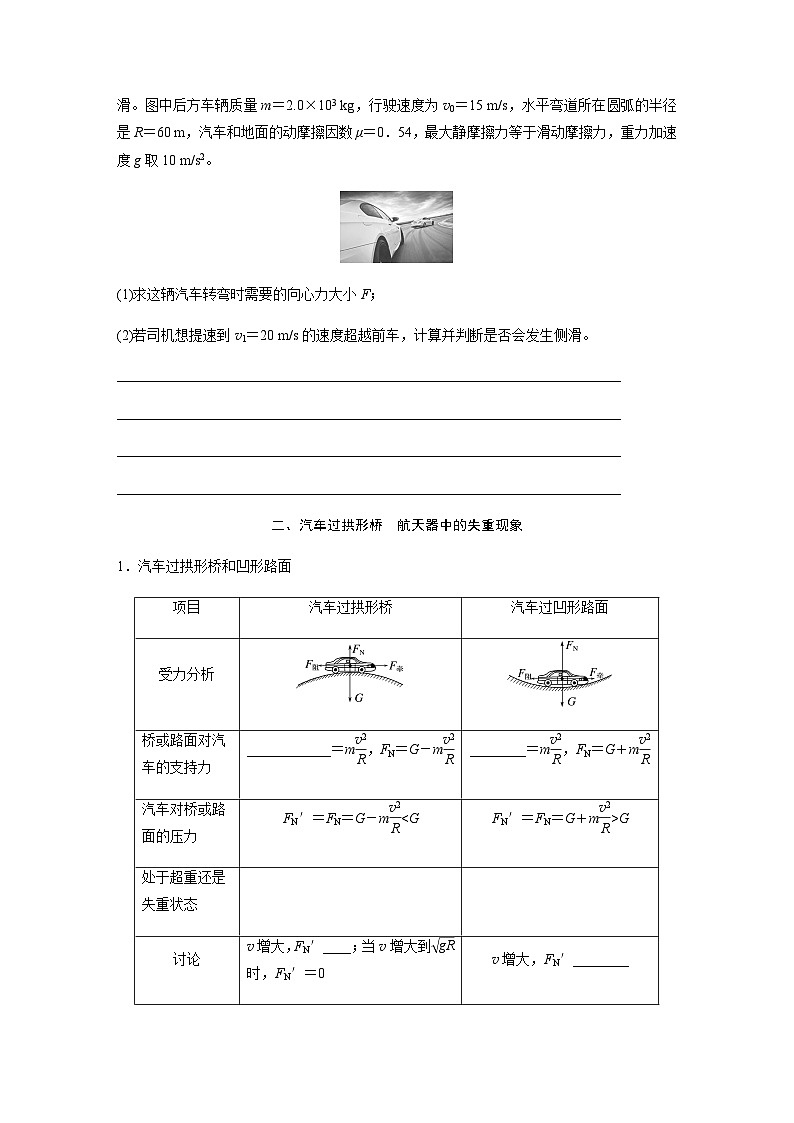
例2 经验丰富的司机一般不会在弯道上超车，因为汽车转弯时如果速度过大，容易发生侧滑。图中后方车辆质量m＝2.0×103 kg，行驶速度为v0＝15 m/s，水平弯道所在圆弧的半径是R＝60 m，汽车和地面的动摩擦因数μ＝0．54，最大静摩擦力等于滑动摩擦力，重力加速度g取10 m/s2。
(1)求这辆汽车转弯时需要的向心力大小F；
(2)若司机想提速到v1＝20 m/s的速度超越前车，计算并判断是否会发生侧滑。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
二、汽车过拱形桥 航天器中的失重现象
1．汽车过拱形桥和凹形路面
2.航天器中的失重现象
(1)在近地圆形轨道上，航天器(包括卫星、飞船、空间站)的重力提供向心力，满足关系：mg＝meq \f(v2,R)，则v＝eq \r(gR)。
(2)质量为m′的航天员，受到的座舱的支持力为FN，则m′g－FN＝eq \f(m′v2,R)。
当v＝eq \r(gR)时，FN＝________，即航天员处于完全失重状态。航天器内的任何物体都处于完全失重状态。
汽车在桥面最高点即将飞离桥面时所受支持力恰好为0，此时只有重力提供向心力，即mg＝eq \f(mv2,R)，得v＝eq \r(gR)，若超过这个速度，汽车做什么运动？
________________________________________________________________________
例3 在“天宫二号”中工作的航天员可以自由悬浮在空中，处于失重状态，下列分析正确的是( )
A．失重就是航天员不受力的作用
B．失重的原因是航天器离地球太近，从而摆脱了地球引力的束缚
C．失重是航天器独有的现象，在地球上不可能存在失重现象
D．正是由于引力的存在，才使航天员有可能做环绕地球的圆周运动
例4 质量为3×103 kg的汽车，以36 km/h的速度通过圆弧半径为50 m的凸形桥，则：
(1)汽车到达桥最高点时，求桥所受的压力大小，此时汽车处于超重还是失重？
(2)如果设计为凹桥，半径仍为50 m，汽车仍以36 km/h的速度通过，求在最低点时汽车对桥的压力大小，此时汽车处于超重还是失重？(g＝10 m/s2)
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
三、离心运动
1．定义：做圆周运动的物体沿________方向飞出或做________圆心的运动。
2．物体做离心运动的原因
提供向心力的合力突然________，或者合力________提供所需的向心力。
3．离心运动、近心运动的判断
物体做圆周运动时出现离心运动还是近心运动，由实际提供的合力F合和所需向心力(meq \f(v2,r)或mω2r)的大小关系决定。(如图所示)
(1)当F合＝0时，物体沿________方向做________________；
(2)当0(3)当F合＝mω2r时，“提供”等于“需要”，物体做________________；
(4)当F合>mω2r时，“提供”超过“需要”，物体做____________。
4．离心运动的应用和防止
(1)应用：离心干燥器；洗衣机的________；离心制管技术；分离血浆和红细胞的离心机。
(2)防止：转动的砂轮、飞轮的转速不能过高；在公路弯道，车辆不允许超过__________。
例5 在水平公路上行驶的汽车，当汽车以一定速度运动时，车轮与路面间的最大静摩擦力恰好等于汽车转弯所需要的向心力，汽车沿如图所示的圆形路径(虚线)运动，当汽车行驶速度突然增大，则汽车的运动路径可能是( )
A．Ⅰ B．Ⅱ C．Ⅲ D．Ⅳ
4 生活中的圆周运动
[学习目标]
1.会分析火车转弯、汽车过拱形桥等实际运动问题中向心力的来源(重点)。
2.能解决生活中的圆周运动问题(重难点)。
3.了解航天器中的失重现象及其原因。
4.了解离心运动及物体做离心运动的条件，知道离心运动的应用及危害。
一、火车转弯
图甲为摩托车在水平道路上转弯，图乙为火车转弯，图丙为火车轮缘与铁轨，摩托车和火车转弯向心力来源相同吗？铁路弯道处铁轨内外高度相同吗？为什么要这样设计？
答案 来源不同。摩托车转弯时由摩擦力提供向心力。外轨较高一些，若内外轨高度相同，外轨对轮缘的弹力提供火车转弯的向心力，火车质量太大，轮缘与外轨间的相互作用力太大，铁轨和车轮极易受损，需要设计外轨高于内轨，使火车受到的重力、支持力的合力提供向心力。
1.铁路弯道的特点
铁路弯道处，外轨高于内轨，若火车按规定的速度v0行驶，转弯所需的向心力完全由重力和支持力的合力提供，即mgtan θ＝meq \f(v02,R)，如图所示，则v0＝eq \r(gRtan θ)，其中R为弯道半径，θ为轨道平面与水平面间的夹角(θ很小的情况下，tan θ≈sin θ)。
2．汽车转弯特点
(1)水平弯道：由静摩擦力提供向心力，汽车速度最大时，μmg＝eq \f(mvm2,R)，可得vm＝eq \r(μgR)。
(2)增大汽车安全转弯速度的有效方法
①增大转弯半径。
②把转弯处设计成外高内低(填“外高内低”或“外低内高”)路面(类似火车转弯)。
若v0为火车不受轨道侧压力的临界速度，当火车不按规定速度行驶时，对铁轨有什么影响？
答案 若v>v0，轮缘受到外轨向内的挤压力，外轨易损坏。
若v例1 如图所示，在修筑铁路时，弯道处的外轨会略高于内轨。当火车以规定的行驶速度转弯时，内、外轨均不会受到轮缘的挤压，设此时火车的速度大小为v，重力加速度为g，两轨所在平面的倾角为θ，则下列说法不正确的是( )
A．该弯道的半径r＝eq \f(v2,gtan θ)
B．当火车质量改变时，规定的行驶速度大小不变
C．当火车速率大于v时，内轨将受到轮缘的挤压
D．当火车以规定的行驶速度转弯时，向心加速度大小为an＝gtan θ
答案 C
解析 依题意，当内、外轨均不会受到轮缘的挤压时，由重力和支持力的合力提供向心力，
有mgtan θ＝man＝meq \f(v2,r)
解得火车的向心加速度大小及该弯道的半径为
an＝gtan θ，r＝eq \f(v2,gtan θ)
即v＝eq \r(grtan θ)
显然规定的行驶速度与火车质量无关，故A、B、D正确；当火车速率大于v时，重力与支持力的合力不足以提供火车所需向心力，则外轨将受到轮缘的挤压，故C错误。
例2 经验丰富的司机一般不会在弯道上超车，因为汽车转弯时如果速度过大，容易发生侧滑。图中后方车辆质量m＝2.0×103 kg，行驶速度为v0＝15 m/s，水平弯道所在圆弧的半径是R＝60 m，汽车和地面的动摩擦因数μ＝0.54，最大静摩擦力等于滑动摩擦力，重力加速度g取10 m/s2。
(1)求这辆汽车转弯时需要的向心力大小F；
(2)若司机想提速到v1＝20 m/s的速度超越前车，计算并判断是否会发生侧滑。
答案 (1)7 500 N (2)会侧滑
解析 (1)汽车转弯时需要的向心力为
F＝meq \f(v02,R)＝7 500 N
(2)汽车转弯时，静摩擦力提供向心力，汽车受到的最大静摩擦力为Ffm＝μmg＝10 800 N
若司机想提速到v1＝20 m/s的速度超越前车，则需要的向心力为Fn′＝eq \f(mv12,R)≈13 333 N
Fn′>Ffm
汽车会发生侧滑。
二、汽车过拱形桥 航天器中的失重现象
1．汽车过拱形桥和凹形路面
2.航天器中的失重现象
(1)在近地圆形轨道上，航天器(包括卫星、飞船、空间站)的重力提供向心力，满足关系：mg＝meq \f(v2,R)，则v＝eq \r(gR)。
(2)质量为m′的航天员，受到的座舱的支持力为FN，则m′g－FN＝eq \f(m′v2,R)。
当v＝eq \r(gR)时，FN＝0，即航天员处于完全失重状态。航天器内的任何物体都处于完全失重状态。
汽车在桥面最高点即将飞离桥面时所受支持力恰好为0，此时只有重力提供向心力，即mg＝eq \f(mv2,R)，得v＝eq \r(gR)，若超过这个速度，汽车做什么运动？
答案 平抛运动。
例3 在“天宫二号”中工作的航天员可以自由悬浮在空中，处于失重状态，下列分析正确的是( )
A．失重就是航天员不受力的作用
B．失重的原因是航天器离地球太近，从而摆脱了地球引力的束缚
C．失重是航天器独有的现象，在地球上不可能存在失重现象
D．正是由于引力的存在，才使航天员有可能做环绕地球的圆周运动
答案 D
解析 航天器和航天员在太空中受到的引力提供向心力，使航天器和航天员做环绕地球的圆周运动，故A错误，D正确；失重时航天员仍然受到地球引力作用，故B错误；失重是普遍现象，任何物体只要有方向向下的加速度，均处于失重状态，故C错误。
例4 质量为3×103 kg的汽车，以36 km/h的速度通过圆弧半径为50 m的凸形桥，则：
(1)汽车到达桥最高点时，求桥所受的压力大小，此时汽车处于超重还是失重？
(2)如果设计为凹桥，半径仍为50 m，汽车仍以36 km/h的速度通过，求在最低点时汽车对桥的压力大小，此时汽车处于超重还是失重？(g＝10 m/s2)
答案 (1)2.4×104 N 失重 (2)3.6×104 N
超重
解析 (1)汽车到达桥最高点时，速度v＝36 km/h＝10 m/s，竖直方向受重力和支持力，
二力的合力提供向心力有mg－FN＝eq \f(mv2,R)
则支持力为FN＝mg－eq \f(mv2,R)
可得FN＝2.4×104 N
汽车受到的支持力与对桥的压力是相互作用力，所以桥所受的压力大小为2.4×104 N，小于汽车的重力，所以汽车处于失重状态；
(2)最低点时对汽车有FN－mg＝eq \f(mv2,R)
可得FN＝eq \f(mv2,R)＋mg＝3.6×104 N
汽车受到的支持力与对桥的压力是相互作用力，所以桥所受的压力大小为3.6×104 N，大于重力，所以汽车处于超重状态。
三、离心运动
1．定义：做圆周运动的物体沿切线方向飞出或做逐渐远离圆心的运动。
2．物体做离心运动的原因
提供向心力的合力突然消失，或者合力不足以提供所需的向心力。
3．离心运动、近心运动的判断
物体做圆周运动时出现离心运动还是近心运动，由实际提供的合力F合和所需向心力(meq \f(v2,r)或mω2r)的大小关系决定。(如图所示)
(1)当F合＝0时，物体沿切线方向做匀速直线运动；
(2)当0(3)当F合＝mω2r时，“提供”等于“需要”，物体做匀速圆周运动；
(4)当F合>mω2r时，“提供”超过“需要”，物体做近心运动。
4．离心运动的应用和防止
(1)应用：离心干燥器；洗衣机的脱水筒；离心制管技术；分离血浆和红细胞的离心机。
(2)防止：转动的砂轮、飞轮的转速不能过高；在公路弯道，车辆不允许超过规定的速度。
例5 在水平公路上行驶的汽车，当汽车以一定速度运动时，车轮与路面间的最大静摩擦力恰好等于汽车转弯所需要的向心力，汽车沿如图所示的圆形路径(虚线)运动，当汽车行驶速度突然增大，则汽车的运动路径可能是( )
A．Ⅰ B．Ⅱ C．Ⅲ D．Ⅳ
答案 B
解析 当汽车行驶速度突然增大时，最大静摩擦力不足以提供其需要的向心力，则汽车会发生离心运动，即汽车的运动路径可能沿着轨迹Ⅱ，故选B。
项目
汽车过拱形桥
汽车过凹形路面
受力分析
桥或路面对汽车的支持力
____________＝meq \f(v2,R)，FN＝G－meq \f(v2,R)
________＝meq \f(v2,R)，FN＝G＋meq \f(v2,R)
汽车对桥或路面的压力
FN′＝FN＝G－meq \f(v2,R)FN′＝FN＝G＋meq \f(v2,R)>G
处于超重还是失重状态
讨论
v增大，FN′____；当v增大到eq \r(gR)时，FN′＝0
v增大，FN′________
项目
汽车过拱形桥
汽车过凹形路面
受力分析
桥或路面对汽车的支持力
G－FN＝meq \f(v2,R)，FN＝G－meq \f(v2,R)
FN－G＝meq \f(v2,R)，FN＝G＋meq \f(v2,R)
汽车对桥或路面的压力
FN′＝FN＝G－meq \f(v2,R)FN′＝FN＝G＋meq \f(v2,R)>G
处于超重还是失重状态
失重
超重
讨论
v增大，FN′减小；当v增大到eq \r(gR)时，FN′＝0
v增大，FN′增大