初中数学沪科版七年级下册7.2 一元一次不等式图文课件ppt

这是一份初中数学沪科版七年级下册7.2 一元一次不等式图文课件ppt，共20页。PPT课件主要包含了学习目标，新课导入，观察与思考，概念剖析，一元一次不等式的概念，典型例题，当堂检测，解集一定包括了某个解，首先将括号去掉，课堂总结等内容，欢迎下载使用。

1.知道一元一次不等式、不等式的解、不等式的解集、解不等式等概念；2.会解含括号的不等式,并在数轴上表示不等式的解集.(重点)
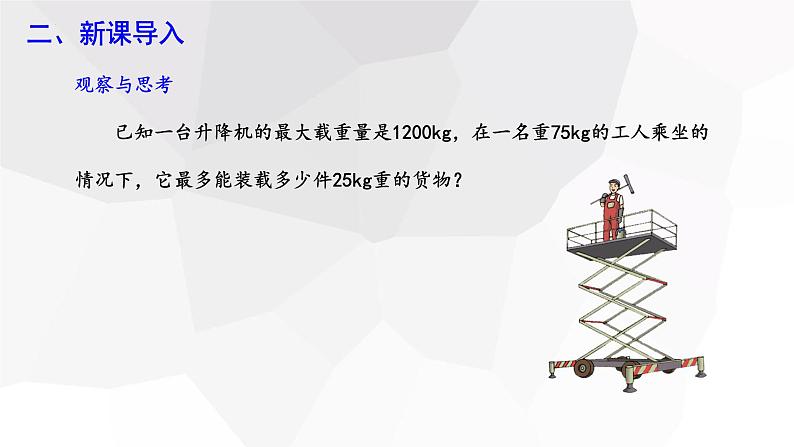
已知一台升降机的最大载重量是1200kg，在一名重75kg的工人乘坐的情况下，它最多能装载多少件25kg重的货物？
前面问题中涉及的数量关系是：
设能载x件25kg重的货物，因为升降机最大载重量是1200kg，所以有 75＋25x≤1200.
工人重 + 货物重 ≤ 最大载重量.
像75 + 25x ≤1200 这样，
它与一元一次方程的定义有什么共同点吗？
含有一个未知数，含未知数的项的次数是1、且不等号两边都是整式的不等式叫作一元一次不等式.
思考：下面给出的数中，能使不等式75 + 25x ≤1200成立吗？你还能找出其他的数吗？
20， 40， 50, 100.
当x=20，75 + 25×20=575<1200, 成立；当x=40，75 + 25×40=1075<1200, 成立；当x=50，75 + 25×50=1325>1200, 不成立；当x=100，75 + 25×100=2575>1200, 不成立.
所有这些解的全体称为这个不等式的解集.
求一个不等式的解集的过程称为解不等式.
一般地，能够使不等式成立的未知数的值，叫做这个不等式的解，
由上可知，小于45的任何一个实数(如20,40等)都是不等式75 + 25x ≤1200的解，而所有这些解的全体(x≤45)称为这个不等式的解集.
注意：不等式的解集必须满足两个条件:1.解集中的任何一个数值都使不等式成立;2.解集外的任何一个数值都不能使不等式成立.
不等式的解与不等式的解集的区别与联系
满足一个不等式的未知数的某个值
满足一个不等式的未知数的所有值
如:x=3是2x-3<7的一个解
如:x<5是2x-3<7的解集
某个解定是解集中的一员
例2.下列说法：①x＝0是2x－1＜0的一个解；②x＝－3不是3x－2＞0的解；③－2x＋1＜0的解集是x＞2.其中正确的是 .
解析：①x＝0时，2x－1＜0成立，所以x＝0是2x－1＜0的一个解；
②x＝－3时，3x－2＞0不成立，所以x＝－3不是3x－2＞0的解；
归纳总结：判断一个数是不是不等式的解，只要把这个数代入不等式，看是否成立．判断一个不等式的解集是否正确，可把这个不等式化为“x＞a”或“x＜a”的形式，再进行比较即可．
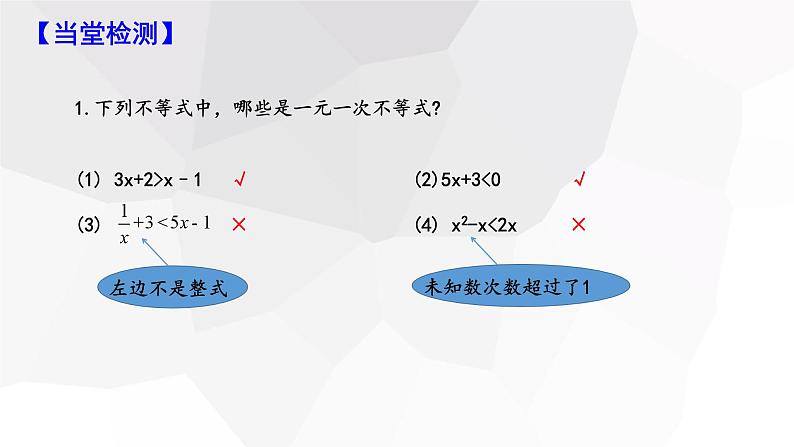
2.判断下列说法是否正确？(1) x=2是不等式x+3<4的解； （ ）(2) 不等式x+1<2的解有无穷多个； （ ）(3) x=3是不等式3x<9的解； （ ）(4) x=2是不等式3x<7的解集. （ ）
例3.解不等式12-6x≥2(1-2x)，并把它的解集在数轴上表示出来.
解：去括号，得 12 -6x ≥ 2-4x，
移项，得 -6x+4x ≥2-12，
根据不等式的基本性质1，将同类项放在一起
合并同类项，得 -2x≥-10，
根据不等式的基本性质2，系数化为1
两边都除以-2，得 x≤5.
原不等式的解集在数轴上表示如图所示.
解集x≤5中包含5，所以在数轴上将表示5的点画成实心圆点.
先在数轴上标出表示2的点A
则点A右边所有的点表示的数都大于2，而点A左边所有的点表示的数都小于2
因此可以像图那样表示3x>6的解集x>2.
容易解得不等式3x＞6的解集是x＞2.
下面以不等式3x＞6为例，详细展示如何将不等式的解集表示在数轴上.
将不等式解集表示在数轴上应遵循以下规律：大于向右画；小于向左画；>、<画空心圆；≥、≤画实心圆.
3.画一画: 利用数轴来表示下列不等式的解集.(1) x＞- 1; (2) x ≤ 1 .
4.解不等式：2x+5≤7(2-x)，并将其解集表示在数轴上.
解：第一步，去括号，得2x+5≤14-7x，第二步，根据不等式的基本性质1，移项，得2x+7x≤14-5，第三步，合并同类项， 得9x≤9，第四步，依据不等式性质2，系数化为1，得x≤1，第五步，将解集x≤1表示在数轴上：
(1)对于含有未知数的不等式，能使不等式成立的 的值，叫做不等式的解．(2)一个含有未知数的不等式的 组成这个不等式的解集．(3)求不等式解集的过程，叫做解不等式．
1.一元一次不等式的概念
含有 未知数，并且未知数的次数都是 的不等式叫做一元一次不等式．