























- 6章末复习 课件+教案 课件 1 次下载
- 7.1不等式及其基本性质(2课时)课件+教案 课件 0 次下载
- 7.3一元一次不等式组(2课时)课件+教案 课件 0 次下载
- 7.4综合与实践 排队问题 课件+教案 课件 0 次下载
- 7 章末复习 课件+教案 课件 0 次下载
数学七年级下册7.2 一元一次不等式优秀ppt课件
展开7.2 一元一次不等式
第1课时 解一元一次不等式
【知识与技能】
1.理解一元一次不等式,不等式的解和解集的概念.
2.掌握一元一次不等式的解法,并能在数轴上表示出一元一次不等式的解集.
【过程与方法】
经历从实际问题中得到一元一次不等式,并探索一元一次不等式的解法,进一步体会数形结合这一重要数学思想的方法.
【情感态度】
让学生在独立思考的基础上,积极参与数学问题的讨论,勇于发表自己的观点,增强合作交流意识,激发学生学习数学的兴趣.
【教学重点】
熟练并准确地解一元一次不等式.
【教学难点】
正确并熟练地运用不等式的基本性质3.
一、情境导入,初步认识
问题某公司的统计资料表明,科研经费每增加1万元,年利润就增加1.8万元.如果该公司原来的年利润为200万元,要使年利润超过245万元,那么增加的科研经费应高于多少万元?
【教学说明】教师提出问题,学生自主探究,然后相互交流,对于有困难的同学,教师可适当给予点拨.
二、思考探究,获取新知
1.一元一次不等式的概念.
问:如果设该公司增加科研经费x万元,能列出怎样的不等式呢?这个不等式会有几个未知数?未知数的次数是几呢?
【教学说明】学生列出不等式后,观察并相互交流,感受一元一次不等式的特征.
【归纳结论】含有一个未知数,未知数的次数是1,且不等号两边都是整式的不等式叫做一元一次不等式.
2.一元一次不等式的解与解集以及解一元一次不等式.
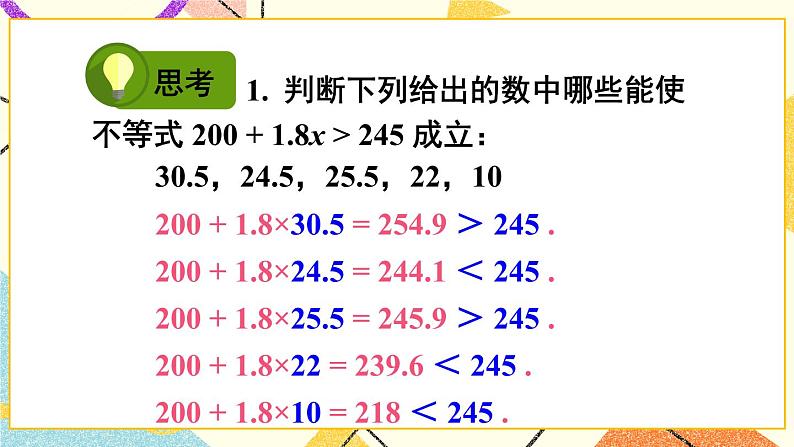
思考:(1)判断下列给出的数中哪些能使不等式200+1.8x>245成立:
30.5,24.5,25.5,22,10.
(2)你还能找出使上述不等式成立的其他数吗?能找多少个?
【教学说明】学生自然联想到一元一次方程,容易想到可用代入检验的方法判断哪些数使不等式成立,哪些使不等式不成立,从而得出一元一次不等式的解(解集)与一元一次方程的解的区别.
【归纳结论】一般地,能够使不等式成立的未知数的值,叫做这个不等式的解,所有这些解的集合称为这个不等式的解集.一元一次方程的解只有一个,一元一次不等式的解有无数个,求不等式解集的过程叫做解不等式.
三、典例精析,掌握新知
例1 解不等式:2x+5≤7(2-x),
【解】去括号,得2x+5≤14-7x,
移项,得2x+7x≤14-5.
合并同类项,得9x≤9.
x系数化成1,得x≤1.
不等式的解集可以在数轴上直观地表示出来,如x≤1,可用数轴上表示1的点以及左边所有点来表示
例2 解不等式,并把它的解集在数轴上表示出来:
【解】去分母,得2(4+x)-6<3x.
去括号,得8+2x-6<3x.
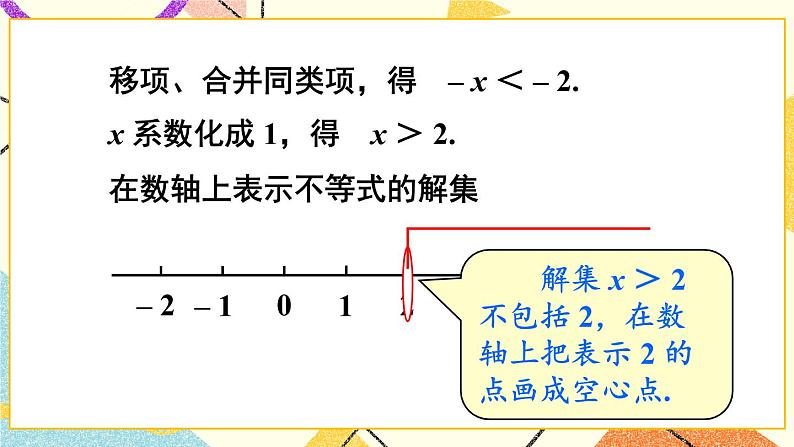
移项,合并同类项,得-x<-2.
x系数化成1,得x>2.在数轴上表示不等式的解集为:
交流:一元一次方程的解法与一元一次不等式的解法有哪些相同点和不同点?为什么解法会有不同?
【教学说明】学生自主探究,然后相互交流,讨论一元一次不等式与一元一次方程解法的异同.
【归纳结论】解一元一次不等式与解一元一次方程的方法与步骤是一样的,也有(1)去分母;(2)去括号;(3)移项,合并同类项;(4)系数化为1等几个步骤,不同之处在于解不等式时,不等式两边同乘以或除以一个负数时,不等号要改变方向.
四、运用新知,深化理解
1.解下列不等式:
(1)x+5>2;(2)2x<-2;(3)15-7x>3x+5;(4)4x-7>2x+5.
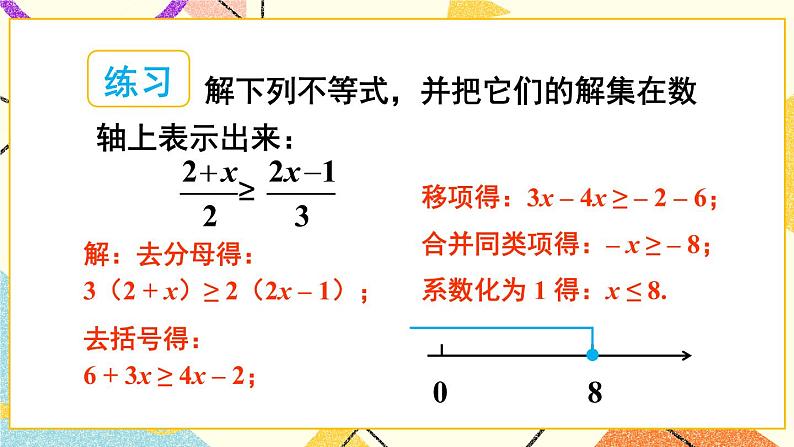
2.解下列不等式,并把它们的解集在数轴上表示出来.
3.设▲,■,●表示三种不同的物体,现用天平称了两次,情况如图所示,那么▲,■,●这三种物体的质量从大到小的顺序排列应为( )
A.■,●,▲ B.■,▲,●
C.▲,●,■ D.▲,■,●
4.当x为何值时,1-的值不小于的值?
5.求不等式3x+16≥5x+8的非负整数解.
6.已知方程组的解x、y满足2x+y≥0,求m的取值范围.
【教学说明】教师给出习题,学生自主完成,教师巡视,对有困难的同学给予指正.
【答案】1.(1)x>-3 (2)x<-1 (3)x<1 (4)x>6
2.(1)去分母得3x+7>5x-5.
移项,合并得-2x>-12.
系数化为1得x<6.
不等式的解集在数轴上表示为:
(2)去分母得2x+1<-5(x-3),
去括号得2x+1<-5x+15,
移项,合并得7x<14,
系数化为:x<2.
不等式的解集在数轴上表示为:
3.D
五、师生互动,课堂小结
通过这节课的学习,你掌握了哪些新知识?还有哪些疑惑?请与同伴交流.
【教学说明】学生相互交流,回顾一元一次不等式的概念及解法,加深所学知识的理解.
完成练习册中本课时练习.
从实际问题中引出一元一次不等式,进而探索一元一次不等式的解法,学生积极主动,从合作交流中获得成功的喜悦,激发学生学习数学的兴趣.
初中沪科版7.2 一元一次不等式课前预习课件ppt: 这是一份初中沪科版<a href="/sx/tb_c27269_t3/?tag_id=26" target="_blank">7.2 一元一次不等式课前预习课件ppt</a>,共22页。PPT课件主要包含了学习目标,新课导入,典型例题,当堂检测等内容,欢迎下载使用。
初中数学沪科版七年级下册7.2 一元一次不等式公开课ppt课件: 这是一份初中数学沪科版七年级下册7.2 一元一次不等式公开课ppt课件,文件包含第3课时一元一次不等式的应用ppt、第1课时一元一次不等式及其解法ppt、第2课时较复杂的一元一次不等式的解法ppt、第1课时解一元一次不等式doc、第2课时一元一次不等式的应用doc等5份课件配套教学资源,其中PPT共55页, 欢迎下载使用。
沪科版七年级下册7.2 一元一次不等式优质课件ppt: 这是一份沪科版七年级下册7.2 一元一次不等式优质课件ppt,文件包含第7章72一元一次不等式第3课时一元一次不等式的实际应用pptx、72一元一次不等式第3课时同步练习docx、第7章一元一次不等式与不等式组72一元一次不等式第3课时docx等3份课件配套教学资源,其中PPT共17页, 欢迎下载使用。














