人教版数学七年级下册 第八章《二元一次方程组 》章节复习课件+章节教学设计+章节复习导学案+单元测试卷（含答案解析）

这是一份人教版数学七年级下册 第八章《二元一次方程组 》章节复习课件+章节教学设计+章节复习导学案+单元测试卷（含答案解析），文件包含人教版数学七年级下册第八章《二元一次方程组》章节复习课件pptx、人教版数学七年级下册第八章《二元一次方程组》章节复习教学设计docx、人教版数学七年级下册第八章《二元一次方程组》章节复习导学案docx等3份课件配套教学资源，其中PPT共53页， 欢迎下载使用。

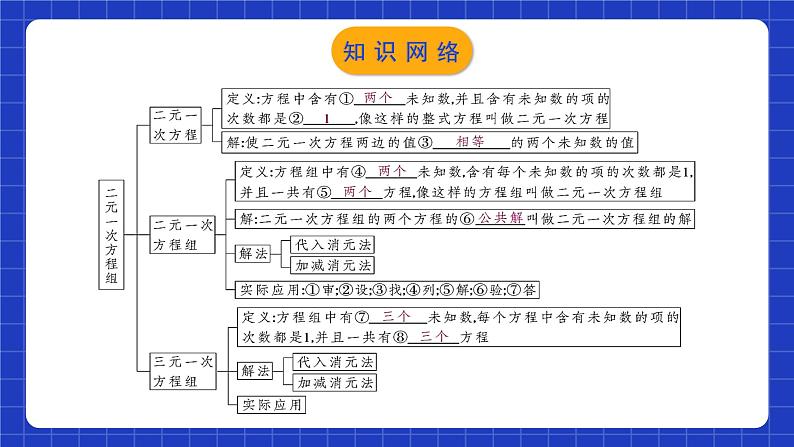
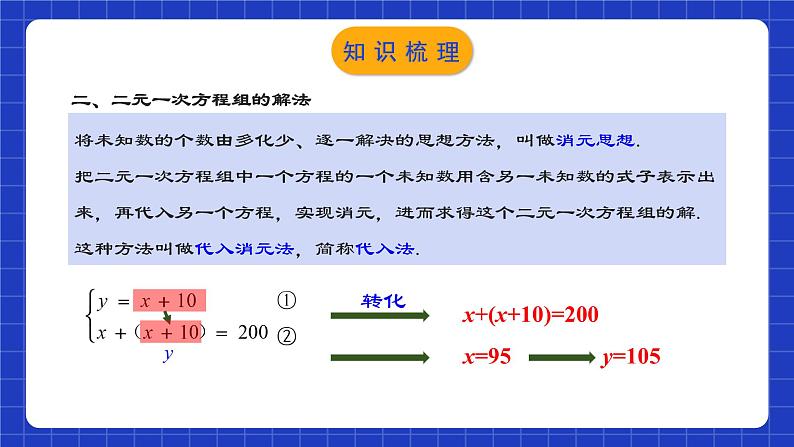
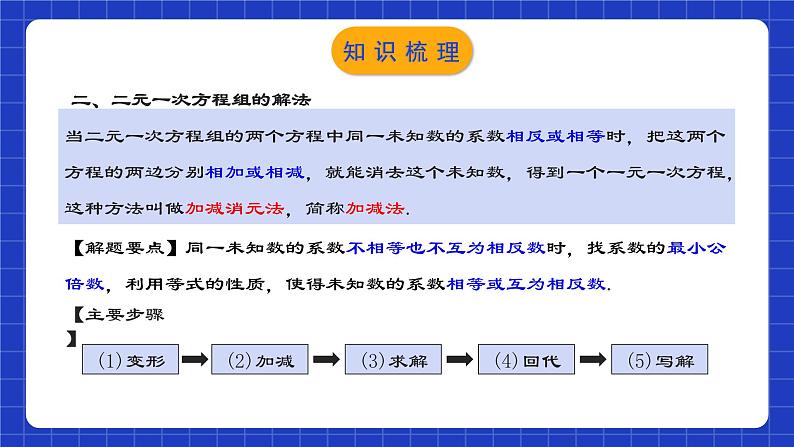
二元一次方程组章节复习学习目标1.正确认识二元一次方程组及其相关的概念.2.理解解方程组的思路，并会用代入法和加减法解二元（或三元）一次方程组.3.学会运用二元一次方程组解决有关应用问题.知识网络 上面两个方程中，每个方程都含有两个未知数(x和y)，并且含有未知数的项的次数都是1，像这样的方程叫做二元一次方程.注：1.“一次”是指含未知数的项的次数是1，而不是未知数的次数； 2.方程的左右两边都是整式.一般地，使二元一次方程两边的值相等的两个未知数的值，叫做二元一次方程的解.一、二元一次方程(组)相关概念知识梳理一般地，二元一次方程组的两个方程的公共解，叫做二元一次方程组的解. 方程组中有两个未知数，含有每个未知数的项的次数都是1，并且一共有两个方程，像这样的方程组叫做二元一次方程组.注：(1) 2个未知数；(2) 未知数的项的次数是1； (3) 方程的左右两边都是整式.一、二元一次方程(组)相关概念知识梳理将未知数的个数由多化少、逐一解决的思想方法，叫做消元思想.把二元一次方程组中一个方程的一个未知数用含另一未知数的式子表示出来，再代入另一个方程，实现消元，进而求得这个二元一次方程组的解. 这种方法叫做代入消元法，简称代入法.二、二元一次方程组的解法知识梳理代入消元法解二元一次方程组的一般步骤：第一步：在已知方程组的两个方程中选择一个适当的方程，将它的某个未知数用含有另一个未知数的式子表示出来；第二步：把此式子代入没有变形的另一个方程中，可得一个一元一次方程；第三步：解这个一元一次方程，得到一个未知数的值；第四步：回代求出另一个未知数的值；第五步：把方程组的解表示出来；第六步：检验(口算或在草稿纸上进行笔算)，即把求得的解代入每一个方程看是否成立.知识梳理当二元一次方程组的两个方程中同一未知数的系数相反或相等时，把这两个方程的两边分别相加或相减，就能消去这个未知数，得到一个一元一次方程，这种方法叫做加减消元法，简称加减法.【解题要点】同一未知数的系数不相等也不互为相反数时，找系数的最小公倍数，利用等式的性质，使得未知数的系数相等或互为相反数. 【主要步骤】二、二元一次方程组的解法知识梳理数量关系字母2代入消元加减消元法三、二元一次方程组的实际应用知识梳理三、二元一次方程组的实际应用实际问题数学问题(二元一次方程组)数学问题的解(二元一次方程组的解)实际问题的答案设未知数列方程组解方程组代入法加减法消元知识梳理考点梳理01二元一次方程(组)的有关概念例1.已知方程(m﹣2)xn﹣1+2y|m﹣1|=m是关于x、y的二元一次方程，求m、n的值．解：∵（m﹣2）xn﹣1+2y|m﹣1|=m是关于x、y的二元一次方程，∴n﹣1=1，|m﹣1|=1，解得：n=2，m=0或2，若m=2，方程为2y=2，不合题意，舍去，则m=0，n=2．考点解析 B【点睛】掌握二元一次方程组满足三个条件：①方程组中的两个方程都是整式方程．②方程组中共含有两个未知数．③每个方程都是一次方程．考点解析  考点解析 CB迁移应用  迁移应用   02 二元一次方程组的解法-代入消元法考点解析例5.若方程5x2m+n+4y3m-2n=9是关于x、y的二元一次方程，求m、n的值.解：根据已知条件可列方程组： ①②考点解析 CA迁移应用【2-3】如果| y+3x -2|+| 5x+2y-2|=0， 求x、y的值.解:根据已知条件，得:由①，得 y=2-3x ③把③代入②，得 5x+2(2-3x)-2=0解这个方程，得 x=2把x=2代入③，得 y=-4所以这个方程组的解是 答: x的值是2，y的值是-4.①②迁移应用例6.用加减法解方程组:(1) (2)①②①②  03 二元一次方程组的解法-加减消元法考点解析例6.用加减法解方程组:(3) (4) ①②①② 考点解析(3) (4) ①②①② 例6.用加减法解方程组:考点解析   B考点解析 CD迁移应用  B迁移应用【3-4】选择适合的解法解下列方程组.(1) (2) (3)①②①②①② 迁移应用【3-4】选择适合的解法解下列方程组.(1) (2) (3)①②①②①②  迁移应用【3-4】选择适合的解法解下列方程组.(1) (2) (3)①②①②①②  迁移应用 04二元一次方程组的特殊解法列举 考点解析【4-1】解方程组 解：由① + ②，得 4(x+y)=36 所以 x+y=9 ③由① - ②，得 6(x-y)=24 所以 x-y=4 ④解由③④组成的方程组解得迁移应用   迁移应用05二元一次方程组的解法的典型应用  考点解析  考点解析  迁移应用  迁移应用06二元一次方程组的实际应用例11.某城市规定：出租车起步价所包含的路程为0～3km，超过3km的部分按每千米另收费. 甲说：“我乘这种出租车走了11km，付了17元.”乙说：“我乘这种出租车走了23km，付了35元.”请你算一算：出租车的起步价是多少元？超过3km后，每千米的车费是多少元？分析：本问题涉及的等量关系有： 总车费=0～3km的车费(起步价)+超过3km的车费.考点解析解 设出租车的起步价是x元,超过3km后每千米收费y元. xx(11-3)y(23-3)y1735考点解析例12.某校现有校舍20000m2，计划拆除部分旧校舍，改建新校舍，使校舍总面积增加30%.若建造新校舍的面积为被拆除的旧校舍面积的4倍，那么应该拆除多少旧校舍，建造多少新校舍？(单位为m2)xm2ym2新校舍面积=被拆除旧校舍面积×4校舍总面积=20000×(1+30%)考点解析 例12.某校现有校舍20000m2，计划拆除部分旧校舍，改建新校舍，使校舍总面积增加30%.若建造新校舍的面积为被拆除的旧校舍面积的4倍，那么应该拆除多少旧校舍，建造多少新校舍？(单位为m2)考点解析例13.随着“低碳生活，绿色出行”理念的普及，新能源汽车正逐渐成为人们喜爱的交通工具，某汽车销售公司计划购进一批新能源汽车尝试进行销售，据了解2辆A型汽车、3辆B型汽车的进价共计80万元；3辆A型汽车、2辆B型汽车的进价共计95万元．(1)求A、B两种型号的汽车每辆进价分别为多少万元？(2)若该公司计划正好用180万元购进以上两种型号的新能源汽车（两种型号的汽车均购买），请你帮助该公司设计购买方案；(3)若该汽车销售公司销售1辆A型汽车可获利8000元，销售1辆B型汽车可获利6000元，在（2）中的购买方案中，假如这些新能源汽车全部售出，哪种方案获利最大？最大利润是多少元？考点解析例13.随着“低碳生活，绿色出行”理念的普及，新能源汽车正逐渐成为人们喜爱的交通工具，某汽车销售公司计划购进一批新能源汽车尝试进行销售，据了解2辆A型汽车、3辆B型汽车的进价共计80万元；3辆A型汽车、2辆B型汽车的进价共计95万元．(1)求A、B两种型号的汽车每辆进价分别为多少万元？ 考点解析(2)若该公司计划正好用180万元购进以上两种型号的新能源汽车（两种型号的汽车均购买），请你帮助该公司设计购买方案； 考点解析(3)若该汽车销售公司销售1辆A型汽车可获利8000元，销售1辆B型汽车可获利6000元，在（2）中的购买方案中，假如这些新能源汽车全部售出，哪种方案获利最大？最大利润是多少元？ 考点解析【6-1】一个两位数，减去它的各位数字之和的3倍，结果是30；这个两位数除以它的各位数字之和，商是5、余数是6．这个两位数是多少？ 迁移应用【6-2】某校为7年级寄宿学生安排宿舍，每间宿舍住5人，则有4人住不下；若每间住6人，则有一间只住4人，求该年级寄宿的学生人数和宿舍间数？ 迁移应用【6-3】小亮与爸爸、爷爷三人年龄之和为120岁，爷爷的年龄比小亮与爸爸年龄之和多12岁，爸爸与小亮年龄之差正好等于爷爷与爸爸年龄之差．他们三人的年龄分别是多少？ 迁移应用【6-4】在长为10m，宽为8m的长方形空地中，沿平行于长方形各边的方向分割出三个全等的小长方形花圃，其示意图如图所示．则小长方形花圃的长和宽分别是多少？ 迁移应用【6-5】如图，飞腾公司从 A 地购进原料若干吨，加工成产品后销往 B 地.已知公路运费为 1.5元/（t·km），铁路运费为 1 元/（t·km），飞腾公司共支付公路运费 750 元，铁路运费 4000 元.根据以上信息计算：购进原料多少吨？加工后销往 B 地的产品为多少吨？解：设购进原料 x t，加工后销往 B 地的产品为 y t.答：购进原料20t.加工后销往B地的产品为10t解得迁移应用【6-6】甲、乙两人同时加工一批零件，前3小时两人共加工126件，后5小时中甲先花了1小时修理工具，之后甲每小时比以前多加工10件，乙由于体力消耗较大，每小时比原来少加工1件，结果在后5小时内，甲比乙多加工了15件，甲、乙两人原来每小时各加工多少件？ 迁移应用【6-7】某人用24000元买进甲、乙两种股票，如果甲股票升值15％，乙股票下跌10％时卖出，共获利1350元，试问某人买的甲、乙两股票各是多少元？ 迁移应用【6-8】某商场以一定的进价购迸一批服装，并以一定的单价出售，平均每天卖出10件，30天共获利15000元， 现在为了尽快回笼资金，商场决定将每件衣服降价20%出售，结果平均每天比降价前多卖10件，这样30天可获利12000元，问这批衣服每件的进价及降价前出售的单价各是多少? 迁移应用课程结束