湖南省衡东县第一中学2019-2020学年高二下学期期末考试 数学试题

这是一份湖南省衡东县第一中学2019-2020学年高二下学期期末考试 数学试题，共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

总分：150分 时量：120分钟
一、选择题：本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．已知函数的定义域，的定义域为，则=
A． B．C．D．
2．已知命题，，则
A．，B．，
C．，D．，
3．已知是等差数列，，其前10项和，则其公差
A． B．C．D．
4．已知平面向量，则向量
A． B．C．D．
5．在△ABC中，角A、B、C所对的边分别为a、b、c，且b2＋c2＝a2＋bc，若sinBsinC＝sin2A，则△ABC的形状是
A．等腰三角形B．直角三角形C．等边三角形D．等腰直角三角形
6．已知圆O1：(x－a)2+(y－b)2=4；O2：(x－a－1)2+(y－b－2)2=1 (a、b∈R)，那么两圆的位置关系是
A．内含 B．内切 C．相交 D．外切
7．在平面直角坐标系xOy中，双曲线中心在原点，焦点在y轴上，一条渐近线方程为x－2y＝0，则它的离心率为
2 2 3 4
x y 9 9
0 1
A． B． C． D．
8．某同学10次测评成绩的数据如茎叶图所示，总体的中位数为12，若要使该总体的标准差最小，则4x＋2y的值是
A．12B．14
C．16D．18
9．设某大学的女生体重y(单位：kg)与身高x(单位：cm)具有线性相关关系，根据一组样本数据(xi，yi)(i＝1,2，…，n)，用最小二乘法建立的回归方程为eq \(y,\s\up6(^))＝0.85x－85.71，则下列结论中不正确的是
A．y与x具有正的线性相关关系
B．回归直线过样本点的中心(，)
C．若该大学某女生身高增加1 cm，则其体重约增加0.85 kg
D．若该大学某女生身高为170 cm，则可断定其体重必为58.79 kg
10．设函数 QUOTE \* MERGEFORMAT 则满足的取值范围是
A． B．C．D．
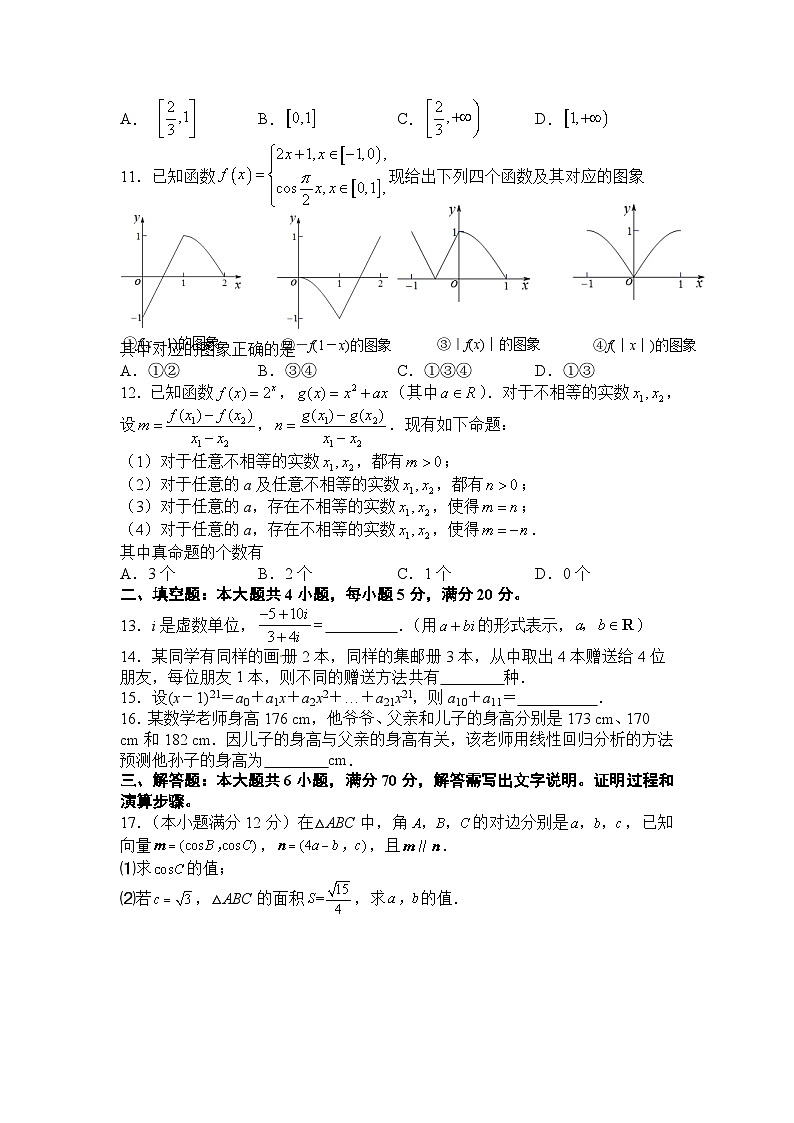
11．①f(x－1)的图象
②－f(1－x)的图象
③｜f(x)｜的图象
④f(｜x｜)的图象
已知函数现给出下列四个函数及其对应的图象

其中对应的图象正确的是
A．①②B．③④C．①③④D．①③
12．已知函数，（其中）．对于不相等的实数，设，．现有如下命题：
（1）对于任意不相等的实数，都有；
（2）对于任意的a及任意不相等的实数，都有；
（3）对于任意的a，存在不相等的实数，使得；
（4）对于任意的a，存在不相等的实数，使得．
其中真命题的个数有
A．3个B．2个C．1个 D．0个
二、填空题：本大题共4小题，每小题5分，满分20分。
13．i是虚数单位， ．（用的形式表示，）
14．某同学有同样的画册2本，同样的集邮册3本，从中取出4本赠送给4位朋友，每位朋友1本，则不同的赠送方法共有 种．
15．设(x－1)21＝a0＋a1x＋a2x2＋…＋a21x21，则a10＋a11＝ ．
16．某数学老师身高176 cm，他爷爷、父亲和儿子的身高分别是173 cm、170 cm和182 cm．因儿子的身高与父亲的身高有关，该老师用线性回归分析的方法预测他孙子的身高为 cm．
三、解答题：本大题共6小题，满分70分，解答需写出文字说明。证明过程和演算步骤。
17．（本小题满分12分）在△ABC中，角的对边分别是，已知向量，，且．
⑴求的值；
⑵若，△ABC的面积，求的值．
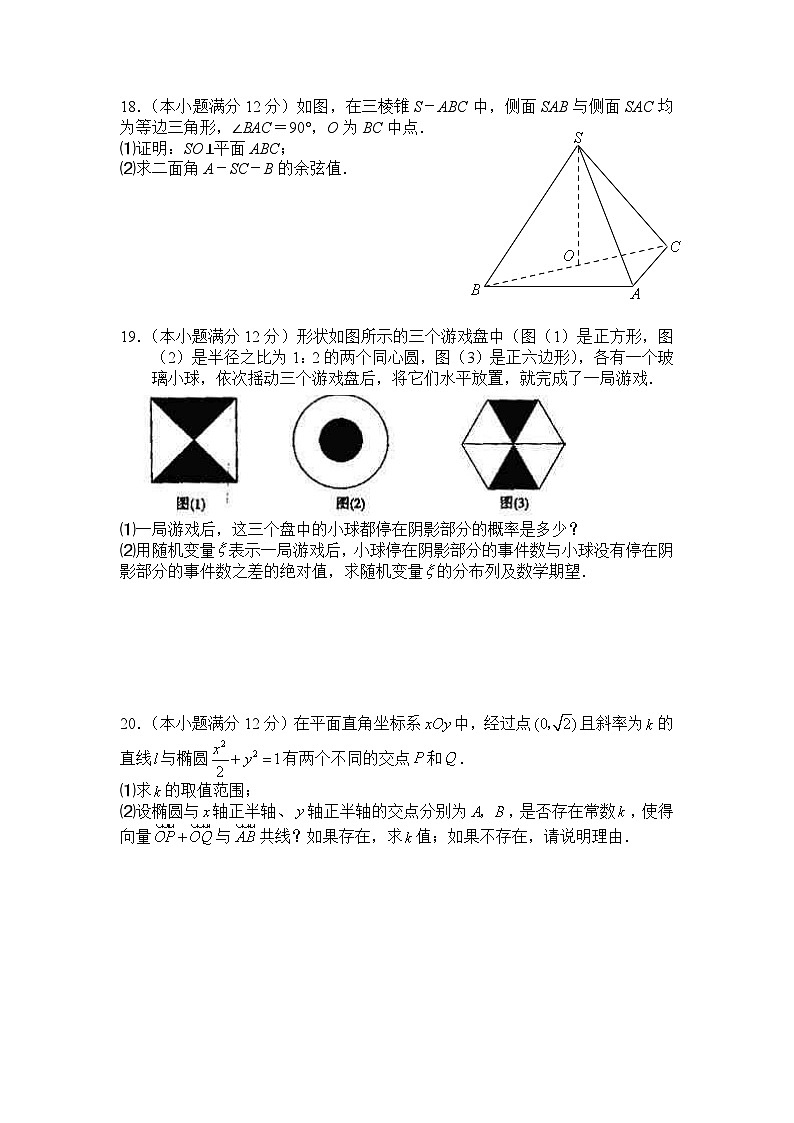
18．（本小题满分12分）如图，在三棱锥S－ABC中，侧面SAB与侧面SAC均为等边三角形，∠BAC＝90°，O为BC中点．
⑴证明：SO⊥平面ABC；
⑵求二面角A－SC－B的余弦值．
19．（本小题满分12分）形状如图所示的三个游戏盘中（图（1）是正方形，图（2）是半径之比为1：2的两个同心圆，图（3）是正六边形），各有一个玻璃小球，依次摇动三个游戏盘后，将它们水平放置，就完成了一局游戏．
⑴一局游戏后，这三个盘中的小球都停在阴影部分的概率是多少？
⑵用随机变量表示一局游戏后，小球停在阴影部分的事件数与小球没有停在阴影部分的事件数之差的绝对值，求随机变量的分布列及数学期望．
20．（本小题满分12分）在平面直角坐标系中，经过点且斜率为的直线与椭圆有两个不同的交点和．
⑴求的取值范围；
⑵设椭圆与轴正半轴、轴正半轴的交点分别为，是否存在常数，使得向量与共线？如果存在，求值；如果不存在，请说明理由．
21．（本小题满分12分）已知函数f(x)＝
⑴当a为何值时，x轴为曲线 的切线；
⑵用min{m，n}表示m，n 中的最小值，设函数 ，讨论h(x)零点的个数
请在第22，23两题中任选一题作答．如果多做，则按所做的第一题记分，作答时请写清题号．
22．（本小题满分10分）选修4-4：坐标系与参数方程
在直角坐标系xOy中，曲线（t为参数，），其中，在以O为极点，x轴正半轴为极轴的极坐标系中，曲线，曲线．
⑴求C2与C3交点的直角坐标；
⑵若C2与C1相交于点A，C3与C1相交于点B，求|AB|的最大值．
23．（本小题满分10分）选修4-5：不等式选讲
已知f(x)＝|ax＋1|(a∈R)，不等式f(x)≤3的解集为{x|－2≤x≤1}．
(1)求a的值；
(2)若恒成立，求k的取值范围．
2020年上期高二期末考试数学参考答案
选择题：本大题共12小题，每小题5分，满分60分．
二、填空题:本大题共4小题，每小题5分，满分20分．
13． 14．10 15．0 16．185
三、解答题:本大题共6小题，满分70分．解答须写出文字说明、证明过程和演算步骤．
17．【解析】⑴∵，∴，
由正弦定理，得，
化简，得﹒
∵A＋B＋C＝π，∴﹒
又∵A，∵，∴．
⑵∵C， ，∴．
∵，∴﹒①
∵，由余弦定理得，
∴，②
由①②，得，从而，（舍负），所以，
∴．
18．【证明】⑴由题设，连结，为等腰直角三角形，
所以，且，
又为等腰三角形，故，
且，从而．
所以为直角三角形，．
又．
所以平面．
⑵解法一：取中点，连结，由⑴知，
得．
为二面角的平面角．
由得平面．
所以，又，
故．
所以二面角的余弦值为．
解法二：以为坐标原点，射线分别为轴、轴的正半轴，
建立如图的空间直角坐标系．
设，则．
的中点，．
．
故等于
二面角的平面角．
，
所以二面角的余弦值为．
19．【解析】⑴一局游戏后，三个盘中停在阴影部分分别记为事件A1，A2，A3，
由题意知A1，A2，A3互相独立，且

⑵一局游戏后，小球停在阴影部分的次数可能取值为0，1，2，3，相应的小球没有停在阴影部分的次数可能取值为3、2、1、0，所以可能取值为1、3
则P（=3）=P（A1A2A3）+
所以分布列为：
．
20．【解析】⑴由已知条件，直线的方程为，代入椭圆方程得．
整理得 ①
直线与椭圆有两个不同的交点和等价于，
解得或．即的取值范围为．
⑵设，则，
由方程①，． ②
又． ③
而．
所以与共线等价于，
将②③代入上式，解得．
由⑴知或，故没有符合题意的常数．
21．【解析】⑴设曲线y＝f(x)与x轴相切于点(x0，0)，则f(x0)＝0，，即，解得，
因此，当时，x轴是曲线y＝f(x)的切线．
⑵当时，g(x)＝－lnx<0，从而h(x)＝min{f(x)，g(x)}≤g(x)<0，
∴h(x)在无零点．
当x＝1时，若，则f(1)＝，h(1)＝min{f(1)，g(1)}＝g(1)＝0，
故x＝1是h(x)的零点；
若，则，，
故x＝1不是的零点．
当时，，所以只需考虑在（0，1）的零点个数．
(ⅰ)若或，则在（0,1）无零点，故在（0,1）单调，而，，所以当时，在（0，1）有一个零点；当0时，在（0，1）无零点．
(ⅱ)若，则在（0，）单调递减，在（，1）单调递增，故当=时，取最小值，最小值为=．
①若＞0，即＜＜0，在（0,1）无零点．
②若=0，即，则在（0,1）有唯一零点；
③若＜0，即，由于，，所以当时，在（0,1）有两个零点；当时，在（0,1）有一个零点．
综上，当或时，由一个零点；当或时，有两个零点；当时，有三个零点．
22．【解析】⑴曲线C2的直角坐标方程为x2+y2－2y＝0，曲线C3的直角坐标方程为x2+y2－2x＝0，联立解得或，
所以C2与C3交点的直角坐标为(0，0)和(，)
(2)曲线C1的极坐标方程为，其中．
因此A的极坐标为，的极坐标为．
所以，
当时，取得最大值，最大值为．
23．【解析】⑴由|ax＋1|≤3得－4≤ax≤2．又f(x)≤3的解集为{x|－2≤x≤1}，
所以当a≤0时，不合题意．
当a＞0时，－eq \f(4,a)≤x≤eq \f(2,a)，得a＝2．
(2)记h(x)＝，
则h(x)＝
所以|h(x)|≤1，因此k≥1．
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
C
D
D
C
C
A
A
D
C
D
B
1
3
P