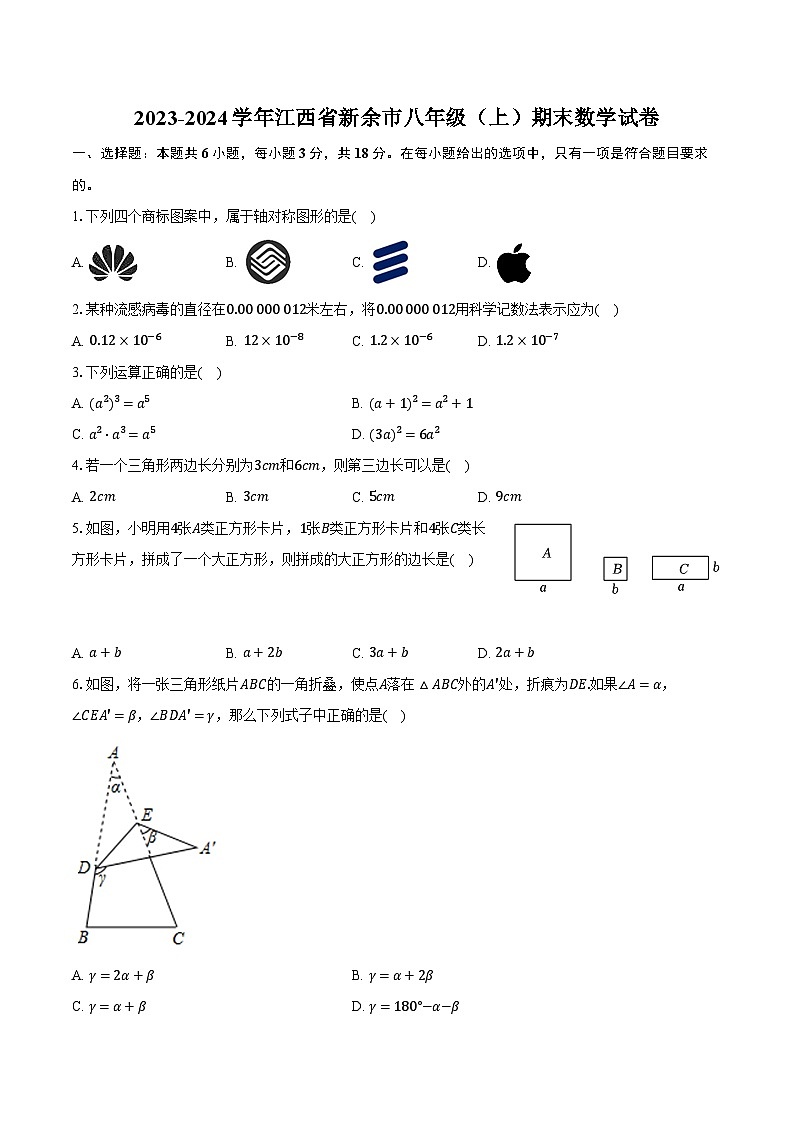
2023-2024学年江西省新余市八年级（上）期末数学试卷（含解析）

这是一份2023-2024学年江西省新余市八年级（上）期末数学试卷（含解析），共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.下列四个商标图案中，属于轴对称图形的是( )
A. B. C. D.
2.某种流感病毒的直径在0.00 000 012米左右，将0.00 000 012用科学记数法表示应为( )
A. 0.12×10−6B. 12×10−8C. 1.2×10−6D. 1.2×10−7
3.下列运算正确的是( )
A. (a2)3=a5B. (a+1)2=a2+1
C. a2⋅a3=a5D. (3a)2=6a2
4.若一个三角形两边长分别为3cm和6cm，则第三边长可以是( )
A. 2cmB. 3cmC. 5cmD. 9cm
5.如图，小明用4张A类正方形卡片，1张B类正方形卡片和4张C类长方形卡片，拼成了一个大正方形，则拼成的大正方形的边长是( )
A. a+bB. a+2bC. 3a+bD. 2a+b
6.如图，将一张三角形纸片ABC的一角折叠，使点A落在△ABC外的A′处，折痕为DE.如果∠A=α，∠CEA′=β，∠BDA′=γ，那么下列式子中正确的是( )
A. γ=2α+βB. γ=α+2β
C. γ=α+βD. γ=180°−α−β
二、填空题：本题共6小题，每小题3分，共18分。
7.计算：99×101= ______．
8.若分式x+1x−2无意义，则x=______．
9.在平面直角坐标系中，点(−3,2)与点(m,n)关于x轴对称，则mn= ______．
10.已知一个正多边形的一个外角为60°，则它的内角和为______．
11.如图，等腰三角形ABC的底边BC长为4，面积为24，腰AC的垂直平分线EF分别交AC，AB于点E，F.若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值为______．
12.如图，已知点O是等边△ABC内一点，∠AOB=130°，∠BOC=α，点D是△ABC外一点，且△ADC≌△BOC，当△AOD是等腰三角形时，α的度数是______．
三、解答题：本题共11小题，共84分。解答应写出文字说明，证明过程或演算步骤。
13.(本小题6分)
(1)计算：20230+(−1)2024−(12)−1；
(2)若am=2，an=3，求am+n的值．
14.(本小题6分)
油纸伞的制作技艺十分巧妙，已列入江西省省级非物质文化遗产.如图，伞圈D沿着伞柄滑动时，总有伞骨BD=CD，AB=AC，从而使得伞柄AP始终平分同一平面内两条伞骨所成的∠BAC.为什么？
15.(本小题6分)
以下是某同学解分式方程3x−2+1=x−3x+2的过程：
解：方程两边同时乘(x+2)(x−2)，得…………①
3(x−2)+(x+2)(x−2)=(x−3)(x+2)…………②
解得x=1…………③
检验：当x=1时，(x+2)(x−2)≠0…………④
所以，原分式方程的解为x=1…………⑤
老师批改后说答案错了，请问是从第______步开始出现错误，请你写出正确的解答过程．
16.(本小题6分)
先化简：a2−25a−2÷(a−5)−a2−2aa2−4a+4，然后在5，2，0这三个数中选取一个合适的数作为a的值代入计算．
17.(本小题6分)
如图，在正五边形ABCDE中，请仅用无刻度的直尺分别按下列要求作图(保留作图痕迹)．
(1)如图1，过点A求作此正五边形的对称轴；
(2)如图2，点M在AB上，且AM=2BM，在AE边上求作一点N，使AN=2EN．
18.(本小题8分)
如图，把长方形纸片ABCD纸沿对角线折叠，重叠部分为△EBD．
(1)求证：△EBD是等腰三角形；
(2)若AB=4，BE=5，求△EBD的面积．
19.(本小题8分)
为了创建国家卫生城市，我县某小区购进A型和B型两种分类垃圾桶，购买A型垃圾桶花费了2500元，购买B型垃圾桶花费了2000元，且购买A型垃圾桶数量是购买B型垃圾桶数量的2倍，已知购买一个B型垃圾桶比购买一个A型垃圾桶多花30元．
(1)求购买一个A型垃圾桶需多少元？
(2)若小区一次性购买A型，B型垃圾桶共60个，要使总费用不超过4000元，最少要购买多少个A型垃圾桶？
20.(本小题8分)
课本再现：如图1，在等腰△ABC中，因为AB=AC，过点A作AD⊥BC于点D，所以△ABD，△ACD均为直角三角形，由AB=AC，AD=AD，可得Rt△ABD≌Rt△ACD(HL)，因此∠B=∠C，∠BAD=∠CAD，BD=CD．
由上面推理我们发现了等腰三角形的两条性质如下：
性质1：等腰三角形的两个底角相等；
性质2：等腰三角形顶角平分线、底边上的中线、底边上的高互相重合(简写成“三线合一”)．
(1)请你在备用图中用添加其他辅助线的方法，证明等腰三角形的这两条性质．
(2)如图2，在△ABC中，AB=AC=BC，运用上述等腰三角形的性质证明：在直角三角形中，30°角所对的直角边等于斜边的一半．
21.(本小题9分)
如图，△ABC的外角∠DAC的平分线交BC边的垂直平分线于P点，PD⊥AB于D，PE⊥AC于E．
(1)求证：BD=CE；
(2)若AB=6cm，AC=10cm，求AD的长．
22.(本小题9分)
整体思想是数学解题中常见的一种思想方法.阅读下列材料：
下面是某同学对多项式(x2+2x)(x2+2x+2)+1进行因式分解的过程.将“x2+2x“看成一个整体，令x2+2x=y，则原式=y2+2y+1=(y+1)2再将“y”还原即可．
解：设x2+2x=y，
原式=y(y+2)+1(第一步)
=y2+2y+1(第二步)
=(y+1)2(第三步)
=(x2+2x+1)2(第四步)
问题：
(1)该同学因式分解的结果不正确，请直接写出正确的结果______；
(2)根据材料，请模仿以上方法尝试对多项式(x2−6x+8)(x2−6x+10)+1进行因式分解；
(3)根据材料，请模仿以上方法尝试计算：
(1−2−3−…−2023)×(2+3+…+2024)−(1−2−3−…−2024)(2+3+…+2023)．
23.(本小题12分)
【阅读理解】
(1)如图1，点A，B，C在同一直线上，DA⊥AC于点A，EC⊥AC于点C，AB=CE，AD=CB，求证：∠BDE=45°；
【拓展应用】
(2)如图2，在平面直角坐标系xOy中，点A(2,1)，B(3,1)，分别连接OA，OB，设OA与x轴正半轴的夹角为α，OB与x轴正半轴的夹角为β，求证：α+β=45°；
【能力提升】
(3)如图3，在平面直角坐标系xOy中，点E(6,3)，EF⊥x轴于点F，设点G为x轴上的一动点，当满足∠EOG+∠GEF=45°时，求OG的长．
答案和解析
1.【答案】A
【解析】解：A、是轴对称图形，故此选项符合题意；
B、不是轴对称图形，故此选项不合题意；
C、不是轴对称图形，故此选项不合题意；
D、不是轴对称图形，故此选项不合题意；
故选：A．
根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．
此题主要考查了轴对称图形，关键是掌握轴对称图形的定义．
2.【答案】D
【解析】【分析】
本题考查用科学记数法表示较小的数，一般形式为a×10−n，其中1≤|a|<10，n为由原数左边起第一个不为零的数字前面的0的个数所决定，绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10−n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．
【解答】
解：0.00000012=1.2×10−7．
故选D．
3.【答案】C
【解析】解：A、(a2)3=a6，此选项错误；
B、(a+1)2=a2+2a+1，此选项错误；
C、a2⋅a3=a5，此选项正确；
D、(3a)2=9a2，此选项错误．
故选：C．
A、根据幂的乘方法则计算；
B、根据完全平方公式计算；
C、根据同底数幂的乘法计算；
D、根据积的乘方法则计算．
本题考查了完全平方公式、同底数幂的乘法、幂的乘方与积的乘方，解题的关键是掌握有关运算法则以及公式．
4.【答案】C
【解析】解：根据题意得，6−3<第三边<6+3，
∴3<第三边<9，
∴第三边可以是5cm．
故选：C．
根据三角形的特性：两边之和大于第三边，三角形的两边的差一定小于第三边，进行解答即可．
此题主要考查了三角形的三边关系，关键是掌握第三边的范围是：大于已知的两边的差，而小于两边的和．
5.【答案】D
【解析】解：由题意得：拼成的大正方形的面积=4a2+4ab+b2
=(2a+b)2，
∴拼成的大正方形的边长是2a+b，
故选：D．
根据题意可得：拼成的大正方形的面积=4a2+4ab+b2=(2a+b)2，即可解答．
本题考查了完全平方式，完全平方公式的几何背景，熟练掌握完全平方公式的特征是解题的关键．
6.【答案】A
【解析】【分析】
本题主要考查了三角形外角性质，根据三角形的外角得：∠BDA′=∠A+∠AFD，∠AFD=∠A′+∠CEA′，代入已知可得结论。
【解答】
解：由折叠得：∠A′=∠A
∵∠BDA′=∠A+∠AFD，∠AFD=∠A′+∠CEA′
∵∠A=α，∠CEA′=β，∠BDA′=γ
∴∠BDA′=γ=α+α+β=2α+β
故选A。
7.【答案】9999
【解析】解：原式=(100−1)(100+1)
=1002−12
=9999．
故答案为：9999．
根据平方差公式即可求出答案．
本题考查平方差公式，解题的关键是熟练运用平方差公式．
8.【答案】2
【解析】解：由题意得：x−2=0，
解得：x=2，
故答案为：2．
根据分式无意义的条件可得x−2=0，再解即可．
此题主要考查了分式无意义的条件，关键是掌握分式无意义的条件是分母等于零．
9.【答案】6
【解析】解：∵点(−3,2)与点(m,n)关于x轴对称，
∴m=−3，n=−2，
∴mn=(−3)×(−2)=6．
故答案为：6．
根据关于x轴的对称点的坐标特点：横坐标不变，纵坐标互为相反数可得m、n的值，进而可得答案．
此题主要考查了关于x轴对称点的性质，掌握关于x轴对称点的横坐标相同，纵坐标互为相反数是解题关键．
10.【答案】720°
【解析】解：多边形的边数为：360°÷60°=6，
正多边形的内角和的度数是：(6−2)×180°=720°，
故答案为：720°．
根据任何多边形的外角和都是360°，利用360°除以外角的度数就可以求出外角和中外角的个数，即多边形的边数．n边形的内角和是(n−2)⋅180°，把多边形的边数代入公式，就得到多边形的内角和．
本题考查了多边形的内角和外角，根据外角和的大小与多边形的边数无关，由外角和求正多边形的边数，是常见的题目，需要熟练掌握．
11.【答案】14
【解析】解：如图，连接AM，AD．
∵AB=AC，CD=DB=12BC=2，
∴AD⊥CB，
∴S△ABC=12⋅BC⋅AD，
∴24=12×4×AD，
∴AD=12，
∵EF垂直平分线段AC，
∴MA=MC，
∴MC+MD=MA+MD≥AD=12，
∴CM+DM的最小值为12，
∴△CDM的周长的最小值为12+2=14．
故答案为：14．
连接AM，AD.利用轴对称的性质求出CM+DM的最小值即可．
本题考查轴对称最短问题，线段的垂直平分线的性质，等腰三角形的性质等知识，解题的关键是掌握轴对称变换的性质，属于中考常考题型．
12.【答案】100°或115°或130°
【解析】解：∵△ABC为等边三角形，
∴∠ACB=60°，
∵△ADC≌△BOC，
∴∠ACD=∠BCO，∠ADC=∠BOC=α，CD=CO，
∴∠ACD+∠ACO=∠BCO+∠ACO，
即∠DCO=∠ACB=60°，
∴△COD为等边三角形，
∴∠COD=∠CDO=60°，
∴∠ADO=∠ADC−∠CDO=α−60°，
当AO=AD时，∠AOD=∠ADC=α−60°，
∵130°+α+60°+α−60°=360°，
解得α=115°；
当AO=DO时，∠DAO=∠ADC=α−60°，
∴∠AOD=180°−2(α−60°)=300°−2α，
∵130°+α+60°+300°−2α=360°，
解得α=130°；
当AD=OD时，∠OAD=∠AOD=12[180°−(α−60°)]=120°−12α，
∵130°+α+60°+120°−12α=360°，
解得α=100°；
综上所述，α的度数为100°或115°或130°．
故答案为：100°或115°或130°．
先根据全等三角形的性质得到∠ACD=∠BCO，∠ADC=∠BOC=α，CD=CO，再证明△COD为等边三角形得到∠COD=∠CDO=60°，所以∠ADO=α−60°，讨论：当AO=AD时，∠AOD=∠ADC=α−60°，利用周角的定义得到130°+α+60°+α−60°=360°；当AO=DO时，∠DAO=∠ADC=α−60°，利用三角形内角和得到∠AOD=300°−2α，利用周角的定义得到130°+α+60°+300°−2α=360°；当AD=OD时，∠OAD=∠AOD=120°−12α，利用周角的定义得到130°+α+60°+120°−12α=360°，然后分别解方程得到α的度数．
本题考查了全等三角形的性质：全等三角形的对应边相等；全等三角形的对应角相等．也考查了等腰三角形的性质和等边三角形的性质．
13.【答案】解：(1)原式=1+1−2
=0；
(2)∵am=2，an=3，
∴am+n=am⋅an
=2×3
=6．
【解析】(1)根据零指数幂、负整数指数幂以及有理数乘方的计算方法进行计算即可；
(2)根据同底数幂乘法的计算方法进行计算即可．
本题考查同底数幂的乘法，零指数幂、负整数指数幂以及有理数乘方，掌握同底数幂的乘法，零指数幂、负整数指数幂以及有理数乘方的计算方法是正确解答的关键．
14.【答案】解：理由：
在△ABD和△ACD中，
AB=ACAD=ADBD=CD，
∴△ABD≌△ACD(SSS)，
∴∠BAD=∠CAD，
即AP平分∠BAC．
【解析】根据三角形“SSS”判定△ABD和△ACD全等，根据全等三角形的性质即可说明．
本题主要考查全等三角形的判定及性质，熟练掌握三角形“边边边”全等判定定理是解决本题的关键．
15.【答案】②
【解析】解：该同学的做法从第②步就出现错误，
故答案为：②；
正确的解法如下：
方程两边同时乘(x+2)(x−2)，得
3(x+2)+(x+2)(x−2)=(x−3)(x−2)，
去括号，得
3x+6+x2−4=x2−5x+6，
移项，得
3x+x2−x2+5x=6−6+4，
合并同类项，得
8x=4，
两边都除以8，得
x=12，
检验：当x=12时，(x+2)(x−2)≠0，
所以，原分式方程的解为x=12．
根据分式方程的解法，依次经过去分母、去括号、移项、合并同类项、系数化为1、检验等步骤求出x的值即可．
本题考查解分式方程，掌握解分式方程的基本步骤，即依次经过去分母、去括号、移项、合并同类项、系数化为1、检验等步骤是解决问题的关键．
16.【答案】解：原式=(a+5)(a−5)a−2⋅1a−5−a(a−2)(a−2)2
=a+5a−2−aa−2
=5a−2，
当a=2，5时，原式无意义，
∴a=0，
当a=0时，原式=50−2=−52．
【解析】根据分式计算过程进行化简，再代入值计算即可．
本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
17.【答案】解：(1)如图，直线AT即为所求；
(2)如图，点N即为所求．

【解析】(1)连接BD，CE交于点T，作直线AT即可；
(2)连接BD，CE交于点T，作直线AT，连接DM交直线AT于点J，连接CJ，延长CJ交AE于点N，点N即为所求，
本题考查作图−轴对称变换，正五边形等知识，解题的关键是掌握轴对称变换的性质．
18.【答案】(1)证明：∵在矩形ABCD中，AD//BC，
∴∠ADC=∠CBD，
∵折叠可得∠CBD=∠C′BD，
∴∠EDB=∠EBD，
∴EB=ED，
∴△EBD是等腰三角形；
(2)解：∵BE=5，
∴DE=BE=5
∵在矩形ABCD中，∠A=90°，
∴S△EBD=12DE⋅AB=12×5×4=10．
【解析】(1)由矩形的性质可得∠ADC=∠CBD，由折叠可得∠CBD=∠C′BD，从而∠EDB=∠EBD，进而得证结论；
(2)直接根据三角形的面积公式即可求解．
本题考查矩形的性质，轴对称，等腰三角形的判定，三角形的面积公式．
19.【答案】解：(1)设购买一个A型垃圾桶需x元，则购买一个B型垃圾桶需(x+30)元，
由题意得：2500x=2000x+30×2，
解得：x=50，
经检验：x=50是原方程的解，且符合题意，
则x+30=80，
答：购买一个A型垃圾桶需50元，一个B型垃圾桶需80元．
(2)设小区一次性购买y个A型垃圾桶，则购买(60−y)个B型垃圾桶，
由题意得：50y+80(60−y)≤4000，
解得：y≥803，
因为y为整数，则y最小为27，
答：最少要购买27个A型垃圾桶．
【解析】(1)设一个A型垃圾桶需x元，则一个B型垃圾桶需(x+30)元，根据购买A型垃圾桶数量是购买B品牌足球数量的2倍列出方程解答即可．
(2)设小区一次性购买y个A型垃圾桶，则购买(60−y)个B型垃圾桶，根据“总费用不超过4000元”列出一元一次不等式并解答即可．
本题考查了分式方程的应用以及一元一次不等式的应用，解题的关键是：(1)找准等量关系，正确列出分式方程；(2)根据各数量之间的关系，正确列出一元一次不等式．
20.【答案】(1)证明：如图1，取BC的中点D，连接AD，则BD=CD，
在△ABD和△ACD中，
AB=ACBD=CDAD=AD，
∴△ABD≌△ACD(SSS)，
∴∠B=∠C，∠BAD=∠CAD，∠ADB=∠ADC=12×180°=90°，
∴AD⊥BC，
∴等腰三角形的两个底角相等；等腰三角形顶角平分线、底边上的中线、底边上的高互相重合(简写成“三线合一”)．
注：答案不唯一，如：
作AD平分∠BAC交BC于点D，则∠BAD=∠CAD，
在△ABD和△ACD中，
AB=AC∠BAD=∠CADAD=AD，
∴△ABD≌△ACD(SAS)，
∴∠B=∠C，BD=CD，∠ADB=∠ADC=12×180°=90°，
∴AD⊥BC，
∴等腰三角形的两个底角相等；等腰三角形顶角平分线、底边上的中线、底边上的高互相重合(简写成“三线合一”)．
(2)证明：如图2，作AE⊥BC于点E，则∠AEB=90°，
∵AB=AC=BC，
∴∠BAC=60°，BE=CE，
∴∠BAE=∠CAE=12∠BAC=30°，
∵BE=12BC，AB=BC，
∴BE=12AB，
∵∠ADB=90°，∠BAD=30°，BE=12AB，
∴在直角三角形中，30°角所对的直角边等于斜边的一半．
【解析】(1)取BC的中点D，连接AD，则BD=CD，即可由AB=AC、BD=CD、AD=AD，根据“SSS“证明△ABD≌△ACD，得∠B=∠C，∠BAD=∠CAD，∠ADB=∠ADC=90°，则AD⊥BC，所以，等腰三角形的两个底角相等；等腰三角形顶角平分线、底边上的中线、底边上的高互相重合(简写成“三线合一”).(答案不唯一，如：作AD平分∠BAC交BC于点D，则∠BAD=∠CAD，可根据“SAS”证明△ABD≌△ACD，得∠B=∠C，BD=CD，∠ADB=∠ADC=90°，则AD⊥BC)
(2)作AE⊥BC于点E，则∠AEB=90°，因为AB=AC=BC，∠BAC=60°，BE=CE，所以∠BAE=∠CAE=12∠BAC=30°，BE=12BC=12AB，即可证明在直角三角形中，30°角所对的直角边等于斜边的一半．
此题重点考查全等三角形的判定与性质、等腰三角形的性质定理的证明等知识，正确地作出辅助线构造全等三角形是解题的关键．
21.【答案】(1)证明：连接BP、CP，
∵点P在BC的垂直平分线上，
∴BP=CP，
∵AP是∠DAC的平分线，且PD⊥AB于D，PE⊥AC于E．
∴DP=EP，
在Rt△BDP和Rt△CEP中，
BP=CPDP=EP,
∴Rt△BDP≌Rt△CEP(HL)，
∴BD=CE；
(2)解：在Rt△ADP和Rt△AEP中，
AP=APDP=EP,
∴Rt△ADP≌Rt△AEP(HL)，
∴AD=AE，
∵AB=6cm，AC=10cm，
∴6+AD=10−AE，
即6+AD=10−AD，
解得AD=2cm．
【解析】本题考查了角平分线上的点到角两边的距离相等的性质，线段垂直平分线上的点到两端点的距离相等的性质，全等三角形的判定与性质，熟记性质并作辅助线构造出全等三角形是解题的关键．
(1)连接BP、CP，根据线段垂直平分线上的点到两端点的距离相等可得BP=CP，根据角平分线上的点到角的两边距离相等可得DP=EP，然后利用“HL”证明Rt△BDP和Rt△CEP全等，根据全等三角形对应边相等证明即可；
(2)利用“HL”证明Rt△ADP和Rt△AEP全等，根据全等三角形对应边相等可得AD=AE，再根据AB、AC的长度表示出BD、CE，然后解方程即可．
22.【答案】(x+1)4
【解析】解：(1)①设x2+2x=y．
原式=y(y+2)+1(第一步)
=y2+2y+1(第二步)
=(y+1)2(第三步)
=(x2+2x+1)2(第四步)
=(x+1)4，
故答案为：(x+1)4；
②设x2−6x=y，
原式=(y+8)(y+10)+1
=y2+18y+80+1
=(y+9)2
=(x2−6x+9)2
=(x−3)4；
(2)设1−2−3−…−2023=y，
原式=y(2+3+…+2024)−(y−2024)(2+3+…+2023)
=y(2+3+…+2024)+2024y−y(2+3+…+2023)+2024(2+3+…+2023)
=2024y+2024(2+3+…+2023)
=2024(y+2+3+…+2023)
=2024(1−2−3−…−2020+2+3+…+2023)
=2024×1
=2024．
(1)①最后再利用完全平方公式将结果分解到不能分解为止；
②根据材料，用换元法进行分解因式；
(2)设1−2−3−…−2023=y，则原式=2024(y+2+3+…+2023)，再将y代入即可求解．
本题考查了因式分解−换元法，公式法，也是阅读材料问题，熟练掌握利用公式法分解因式是解题的关键．
23.【答案】(1)证明：∵DA⊥AC，EC⊥AC，
∴∠A=∠C=90°，
∵AB=CE，AD=CB，
∴△ABD≌△CEB(SAS)，
∴BD=BE，∠CBE=∠ADB，
∵∠ADB+∠ABD=90°，
∴∠ABD+∠CBE=90°，
∴∠DBE−90°，
∴∠BDE=∠BED=12×90°=45°；
(2)证明：作点B关于x轴的对称点C，连接AC，OC，如图所示：

根据对称性可知，∠COD=∠BOD=β，
∵B(3,1)，
∴C(3,−1)，
∵A( 2,1)．
∴AC= (3−2)2+(−1−1)2= 5，OA= 22+12= 5，OC= 32+(−1−0)2= 10．
∴AC2+OA2=OC2，
∴△OAC为直角三角形，∠OAC=90°，
∵OA=AC，
∴∠COA=∠ACO=12×90°=45°，
∴∠AOD+∠COD=∠AOC=45°，
∴a+β=45°．
(3)取OF中点H，连接EH并延长，取HM=EH，连接MF，过点F作FN⊥EM于点N，如图所示：

∵E(6,3)，
∴EF=3，OF=6，
∵OF中点为H，
∴OH=FH=12OF=3，
∵EF⊥OG，
∴∠EFH=∠EFG=90°，
∴△EFH为等腰直角三角形，
∴EH= 2EF=3 2=MH，∠EHF=∠HEF=45°，
∵FN⊥EH，
∴EN=NH=FN=12EH=3 22，
∴MN=MH+HN=9 22，
∵EH=MH，∠OHE=∠MHF，OH=FH，
∴△OHE≌△FHM(SAS)，
∴∠OEH=∠M．
∵∠EOG+∠OEH=∠EHF=45°，∠EOG+∠GEF=45°，
∴∠OEH=∠GEF，
∴∠M=∠GEF，
∵∠MNF=∠EFG=90°，
∴△MNF∽△EFG，
∴MNEF=NFFG，即9 223=3 22FG，
解得：FG=1，
∴OG=OF+FG=6+1=7．
【解析】(1)证明△ABD≌△CEB，得出BD=BE，∠CBE=∠ADB，根据∠ADB+∠ABD=90°，得出∠ABD+∠CBE=90°，求出∠DBE=90°，根据等腰三角形的性质即可证明；
(2)作点B关于x轴的对称点C，连接AC，OC，根据对称性得出∠COD=∠BOD=β，根据两点间距离公式求出AC，OA，根据勾股定理的逆定理得出∠OAC=90°，再根据等腰三角形性质求出∠COA=∠ACO=45°，即可求解；
(3)取OF中点H，连接EH并延长，取HM=EH，连接MF，过点F作FN⊥EM于点N，证明△EFH为等腰直角三角形，得出EH，∠EHF=∠HEF=45°，证明△OHE≌△FHM，得出∠OEH=∠M，证明△MNF∽△EFG，求出FG=1，即可求解．
本题主要考查了三角形全等的判定和性质，坐标与图形，三角形相似的判定和性质，等腰三角形的判定和性质，直角三角形的性质，勾股定理及其逆定理，解题的关键是作出辅助线，熟练掌握三角形全等和三角形相似的判定方法．