
高中湘教版(2019)1.2 导数的运算教学设计
展开【课程标准要求】
利用导数的概念推导出函数的和差积法则。
【教学目标】
1、让学生经历求函数的和差积的求导法则的推导过程,培养学生分析、抽象等思维能力,提升数学运算与数学抽象核心素养.
2、这一节将重心放在运用导数公式来求函数的导数上,与前面运用导数定义的方法形成对比,从而让学生感受求导公式带来的便利性,增强学生学习导数的信心,激发学生学习兴趣,引导学生领悟特殊与一般、有限与无限,量变与质变的辩证关系,感受数学的统一美,意识到数学的应用价值,提升直观想象和逻辑推理核心素养.
【学情与内容分析】
本节内容,一是通过前面计算过的导数,由导数定义可以算出的导数,观察发现进而用导数定义证明得到:函数常数倍的导数,等于常数乘函数的导数;二是前面计算具体函数的导数,观察发现并且证明得到:和函数的导数等于两函数的导数和,差函数的导数等于两函数的导数差;三是利用导数定义,发现证明得到函数乘积的导数. 四是能运用导数的几何意义结合导数的和差积运算法则,求过曲线上一点的切线方程.这节课从已知的具体函数出发,通过观察猜想、尝试探究、类比归纳、推理证明,得到函数和差积的求导法则,这对落实核心素养的培养要求将产生积极的意义. 课程标准对本节课内容未提出具体要求,但湘教版教材开设一节专题学习,彰显了湘教版教材注重数学本质的教学,强调数学思想内涵的理解和应用,注重数学核心素养的培养.
【教学准备】希沃课件。
【难重点】
重点:理解函数的和、差、积的求导法则;加深对积的求导法则理解,强调“先化简变形,再实施求导”的基本思想方法;能运用法则求简单函数的导数.
难点:函数的和、差、积的求导法则的灵活应用.
【教学过程】
【板书设计】
【评价设计】
【作业设计】
完成导学案内容;
教材P23 1、2题
【教学反思】
教学环节
教学内容
师生活动
设计意图
㈠ 复习引入
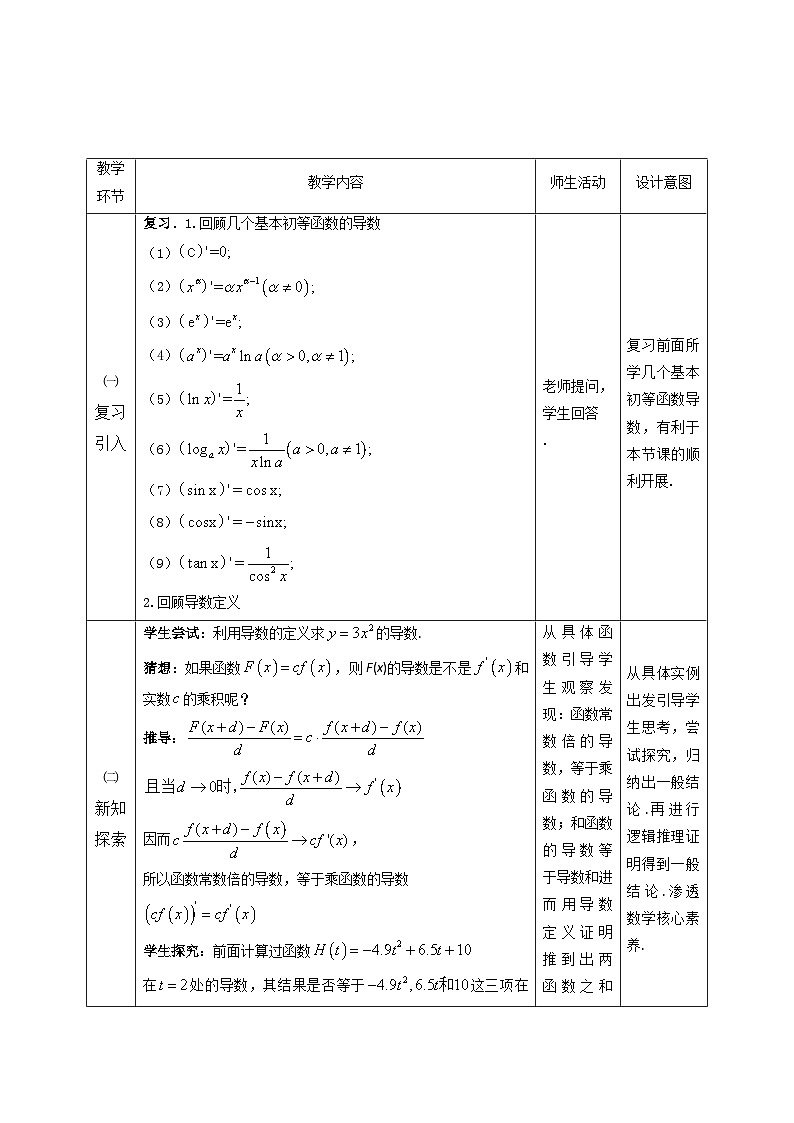
复习.1.回顾几个基本初等函数的导数
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
2.回顾导数定义
老师提问,学生回答
.
复习前面所学几个基本初等函数导数,有利于本节课的顺利开展.
㈡
新知探索
学生尝试:利用导数的定义求的导数.
猜想:如果函数,则F(x)的导数是不是和实数的乘积呢?
推导:
因而,
所以函数常数倍的导数,等于乘函数的导数
学生探究:前面计算过函数
在处的导数,其结果是否等于这三项在处的导数之和呢?你发现了什么?
猜想:和函数的导数等于两函数的导数和.
推导:定义法.
即两函数之和的求导法则为
类似地,两函数之差的求导法则为
从具体函数引导学生观察发现:函数常数倍的导数,等于乘函数的导数;和函数的导数等于导数和.进而用导数定义证明推到出两函数之和的导数.
引导学生采用类比思想,得到两函数之差的求导法则.
从具体实例出发引导学生思考,尝试探究,归纳出一般结论.再进行逻辑推理证明得到一般结论.渗透数学核心素养.
㈢ 典例剖析
例1.求曲线在与直线相交处的切线方程.
给出例1,引导学生直接利用导数的运算法则解决问题.
教师板书,形成示范.
例1帮助学生掌握函数和差的求导法则的灵活应用,进一步提升核心素养.
㈣
新知探索
问题:我们如何能得到的导数呢?
结合导数定义,经过推导,
我们可得函数乘积的求导法则为
师生一起推导,结合函数导数的定义,得出函数乘积的导数法则.
通过引导,学生完全可以自主的推导出函数乘积的求导法则.
㈤ 典例剖析
例2.求函数的导数
方法:熟练使用函数乘积的求导法则.
学生动手,老师纠正.
旨在让学生熟练使用函数乘积的求导法则.
= 6 \* GB4 ㈥
练习巩固
练习1. 求曲线平行于轴的切线方程.
练习2. 求下列函数的导数:
;
;
.
给出练习1、2,请学生在学案、或书、或练习纸上写出各题答案,然后利用希沃授课助手,依次展示两个学生练习,请其余学生纠正错误,指出相关知识点.
练习1强化函数的导数和差积的求导法则.
练习2强化导数的法则的灵活运用.
= 7 \* GB4 ㈦ 归纳小结
本节课有哪些收获?
让学生回忆本节课有哪些收获.
系统梳理整节课所学内容.
(例1过程)
(例2关键过程)
(练习1、练习2关键过程)
希沃课件投影区域
导数的运算法则和推导过程的书写
高中数学湘教版(2019)选择性必修 第二册1.2 导数的运算教案设计: 这是一份高中数学湘教版(2019)选择性必修 第二册<a href="/sx/tb_c4018225_t8/?tag_id=27" target="_blank">1.2 导数的运算教案设计</a>,共6页。教案主要包含了课程标准要求,教学目标,学情与内容分析,教学准备,教学过程,板书设计,评价设计,作业设计等内容,欢迎下载使用。
高中数学湘教版(2019)选择性必修 第二册1.2 导数的运算教学设计: 这是一份高中数学湘教版(2019)选择性必修 第二册<a href="/sx/tb_c4018225_t8/?tag_id=27" target="_blank">1.2 导数的运算教学设计</a>,共4页。教案主要包含了课程标准要求,教学目标,学情与内容分析,教学准备,教学过程,板书设计,评价设计,作业设计等内容,欢迎下载使用。
高中数学北师大版 (2019)选择性必修 第二册第二章 导数及其应用5 简单复合函数的求导法则教学设计: 这是一份高中数学北师大版 (2019)选择性必修 第二册第二章 导数及其应用5 简单复合函数的求导法则教学设计,共3页。教案主要包含了新课导入,新知探究,应用举例,课堂练习,课堂小结,布置作业等内容,欢迎下载使用。













