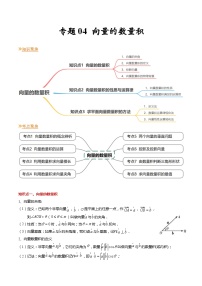
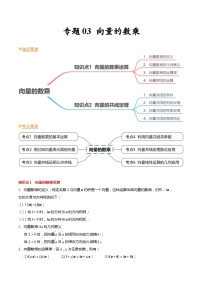
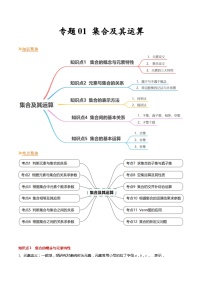
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题06+向量坐标表示与应用(10大考点,知识串讲+热考题型+专题训练)-讲义 试卷 0 次下载
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题07+向量的应用(8大考点,知识串讲+热考题型+专题训练)-讲义 试卷 0 次下载
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题09+二倍角的三角函数(6大考点,知识串讲+热考题型+专题训练)-讲义 试卷 0 次下载
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题10+几个三角恒等式(6大考点,知识串讲+热考题型+专题训练)-讲义 试卷 0 次下载
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题11+余弦定理(6大考点,知识串讲+热考题型+专题训练)-讲义 试卷 0 次下载
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题08+两角和与差的三角函数(10大考点,知识串讲+热考题型+专题训练)-讲义
展开知识聚焦
考点聚焦
知识点1 两角和与差的余弦公式
1、两角和的余弦公式::
2、两角差的余弦公式::
3、使用注意事项:
(1)公式中,都是任意的,既可以是一个角,也可以是几个角的组合;
(2)一般不成立,但在特殊情况下也可能成立。例如:当,时,;
(3)要掌握公式的逆用,如
知识点2 两角和与差的正弦公式
1、两角和的正弦公式::
2、两角差的正弦公式::
3、使用注意事项:
(1)公式中的,都是任意角;
(2)一般情况下,两角和与差的正弦公式不能按分配律展开,即;
(3)注意公式的逆向运用:如
知识点3 两角和与差的正切公式
1、两角和的正切公式::.
2、两角差的正切公式::.
3、使用注意事项:
(1)公式的适用范围是使公式两边有意义的角的取值范围;
(2)公式的变形:;
知识点4 两角和与差的三角函数应用
1、三角函数给角求值与给值求值问题
“给角求值”、“给值求值”问题求解的关键在于“变角”,使其角相同或具有某种关系,借助角之间的联系寻找转化方法.
(1)关键是把“所求角”用“已知角”表示.
①当“已知角”有两个时,“所求角”一般表示为两个“已知角”的和或差的形式;
②当“已知角”有一个时,此时应着眼于“所求角”与“已知角”的和或差的关系.
(2)常见的配角技巧:,,
,等.
2、三角函数给值求角问题
实质是转化为“给值求值”,先求角的某一函数值,再求角的范围,最后确定角.
遵照以下原则:(1)已知正切函数值,选正切函数;
(2)已知正、余弦函数值,选正弦或余弦函数;
若角的范围是,选正、余弦皆可;
若角的范围是,选余弦较好;
若角的范围是,选正弦较好.
考点剖析
考点1 两角和与差余弦公式正用
【例1】(2023·海南·高一统考期末)已知,,,则( )
A. B. C. D.
【变式1-1】(2023·江苏镇江·高一扬中市第二高级中学校考期中)已知且都是第二象限角,则( )
A. B. C. D.
【变式1-2】(2023·江苏无锡·高一辅仁高中校考阶段练习)已知为第二象限角,且终边与单位圆的交点的横坐标为,则( )
A. B. C. D.
【变式1-3】(2023·全国·高一专题练习)已知角的终边过点,且.
(1)求的值;
(2)若,,求的值.
考点2 两角和与差余弦公式逆用
【例2】(2023·甘肃兰州·高一统考期中)等于( )
A. B. C. D.
【变式2-1】(2023·广东深圳·高一校考期末)计算:( )
A. B. C. D.
【变式2-2】(2023·黑龙江哈尔滨·高一哈尔滨市第六中学校校考阶段练习)已知,则a的值为( )
A. B. C. D.
【变式2-3】(2023·辽宁抚顺·高一校联考期中)( )
A.0 B. C. D.
【变式2-4】(2023·全国·高一专题练习)求下列各式的值:
(1);
(2);
(3).
考点3 两角和与差正弦公式正用
【例3】(2023·高一课时练习)若,,且,则 .
【变式3-1】(2023·浙江丽水·高一统考期末)若,且,,则 .
【变式3-2】(2023·浙江杭州·高一学军中学校考阶段练习)(多选)在中,,则的值可能是( )
A. B. C. D.
【变式3-3】(2023·辽宁铁岭·高一西丰县高级中学校考期中)在中,,则的值为( )
A.或 B. C. D.或
考点4 两角和与差余弦公式逆用
【例4】(2023·福建三明·高一三明一中校考阶段练习)( )
A.0 B. C. D.1
【变式4-1】(2023·湖南株洲·高一校考阶段练习)( )
A. B. C. D.
【变式4-2】(2023·全国·高一专题练习)计算:( )
A. B. C. D.
【变式4-3】(2023·陕西商洛·高一校考期中)=( )
A. B. C. D.
考点5 两角和与差正切公式正用
【例5】(2023·江苏宿迁·高一校考阶段练习)已知,,则( )
A. B.- C.- D.
【变式5-1】(2023·浙江·高一校联考期中)已知是方程的两个实数根,则( )
A. B. C. D.
【变式5-2】(2023·全国·高一专题练习)已知为锐角,,角的终边上有一点,则( )
A. B. C. D.
【变式5-3】(2023·浙江·高一阶段练习)如图,已知E是矩形ABCD的对角线AC上一动点,正方形EFGH的顶点F,H分别在边AD,EC上,若.则的值为( )
A. B. C. D.
考点6 两角和与差正切公式逆用
【例6】(2023·广西钦州·高一统考期末)( )
A. B.1 C. D.
【变式6-1】(2023·云南玉溪·高一统考期末)( )
A.1 B. C.3 D.
【变式6-2】(2023·高一课时练习)若,则的值为( )
A. B.1 C. D.2
【变式6-3】(2023·江苏南通·高一统考阶段练习)求值: .
考点7 求特殊角的三角函数值
【例7】(2023·高一课时练习)的值是( )
A. B. C. D.
【变式7-1】(2023·辽宁沈阳·高一校联考期末)( )
A. B. C. D.
【变式7-2】(2023·江西赣州·高一校考阶段练习)计算( )
A. B. C. D.
【变式7-3】(2023·全国·高一专题练习)( )
A. B. C. D.
考点8 给值求值问题
【例8】(2023·全国·高一专题练习)已知为锐角,,则 .
【变式8-1】(2023·全国·高一专题练习)已知,,且,,则 .
【变式8-2】(2023·全国·高一专题练习)已知,,,,则的值为( )
A. B. C. D.
【变式8-3】(2023·江苏南京·高一南京市中华中学校考期中)已知,且,,则( )
A. B. C. D.
考点9 给值求角问题
【例9】(2023·高一课时练习)已知都是锐角,且,则 .
【变式9-1】(2023·江西抚州·高二黎川县第二中学校考开学考试)已知锐角满足,则等于( )
A. B.或 C. D.
【变式9-2】(2023·河南南阳·高一统考期末)矩形由如图所示三个全等的正方形拼接而成,令,则( )
A. B. C. D.
【变式9-3】(2023·广东佛山·高一校考阶段练习)已知,,,且,则的值为 .
【变式9-4】(2023·安徽马鞍山·高一当涂第一中学校考期中)已知,,,,则 .
考点10 综合化简问题
【例10】(2023·全国·高一随堂练习)已知,,求.
【变式10-1】(2023·全国·高一随堂练习)求下列各式的值.
(1);
(2)
【变式10-2】(2023·高一课时练习)化简求值:
(1);
(2).
【变式10-3】(2023·浙江·高一校联考阶段练习)已知角的顶点与原点重合,始边与轴的非负半轴重合,它的终边过点.将绕原点逆时针旋转后与角的终边重合.
(1)求的值;
(2)若角满足,求值.
过关检测
一、单选题
1.(2023·浙江嘉兴·高一嘉兴一中校考阶段练习)等于( )
A. B. C. D.
2.(2023·广东佛山·高一北滘中学校考阶段练习)的值为( )
A. B. C. D.
3.(2023·山东枣庄·高一校考阶段练习)的值等于( )
A. B.0 C. D.
4.(2023·湖北黄冈·高一校考阶段练习)α,β都是锐角,且,,则( )
A. B. C. D.
5.(2023·江苏扬州·高一扬州中学校考阶段练习)已知,则( )
A. B. C. D.
6.(2023·江苏盐城·高一射阳中学校考阶段练习)如图,三个相同的正方形相接,则的值是( )
A. B. C. D.
7.(2023·山东淄博·高一淄博实验中学校考阶段练习)已知,,,则( )
A. B. C. D.或
8.(2023·江苏南京·高一南京外国语学校校考阶段练习)化简的结果为( )
A. B. C. D.
二、多选题
9.(2023·贵州黔西·高一校考阶段练习)下列化简结果正确的是( )
A. B.
C. D.
10.(2023·湖北·高一校考阶段练习)下列计算中正确的是( )
A. B.
C. D.
11.(2023·湖北黄冈·高一校考阶段练习)满足 的一组的值是( )
A., B., C., D.,
12.(2023·湖南长沙·高一长沙一中校考阶段练习)已知,下列关系可能成立的有( )
A. B. C. D.
三、填空题
13.(2023·上海奉贤·高一校考阶段练习)若、为锐角,,,则角 .
14.(2023·云南曲靖·高一宣威市第六中学校考阶段练习)已知,,,,则 .
15.(2023·广东深圳·高一深圳中学校考期中) .
16.(2023·江苏徐州·高一统考期中)计算: .
四、解答题
17.(2023·甘肃兰州·高一兰州一中校考阶段练习)计算下列各式:
(1);
(2).
18.(2023·福建三明·高一三明一中校考阶段练习)已知,,,.
(1)求;
(2)求角.
19.(2023·江苏常州·高一常州市北郊高级中学校考开学考试)已知.
(1)求的值;
(2)若,求的值.
20.(2023·安徽滁州·高一校考开学考试)已知,且.
(1)求的值;
(2)求的值.
21.(2023·上海嘉定·高一校考期中)(1)已知,,求;
(2)已知,且,,用,表示,求.
22.(2023·四川绵阳·高一绵阳南山中学校考阶段练习)已知.
(1)若,求的值.
(2)已知.求角的值.
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题11+余弦定理(6大考点,知识串讲+热考题型+专题训练)-讲义: 这是一份【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题11+余弦定理(6大考点,知识串讲+热考题型+专题训练)-讲义,文件包含寒假作业苏教版2019高中数学高一寒假提升训练专题11余弦定理6大考点知识串讲+热考题型+专题训练原卷版docx、寒假作业苏教版2019高中数学高一寒假提升训练专题11余弦定理6大考点知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题07+向量的应用(8大考点,知识串讲+热考题型+专题训练)-讲义: 这是一份【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题07+向量的应用(8大考点,知识串讲+热考题型+专题训练)-讲义,文件包含寒假作业苏教版2019高中数学高一寒假提升训练专题07向量的应用8大考点知识串讲+热考题型+专题训练原卷版docx、寒假作业苏教版2019高中数学高一寒假提升训练专题07向量的应用8大考点知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题06+向量坐标表示与应用(10大考点,知识串讲+热考题型+专题训练)-讲义: 这是一份【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题06+向量坐标表示与应用(10大考点,知识串讲+热考题型+专题训练)-讲义,文件包含寒假作业苏教版2019高中数学高一寒假提升训练专题06向量坐标表示与应用10大考点知识串讲+热考题型+专题训练原卷版docx、寒假作业苏教版2019高中数学高一寒假提升训练专题06向量坐标表示与应用10大考点知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。