



- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题04++向量的数量积(8大考点,知识串讲+热考题型+专题训练)-讲义 试卷 0 次下载
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题05+平面向量基本定理(6大考点,知识串讲+热考题型+专题训练)-讲义 试卷 0 次下载
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题07+向量的应用(8大考点,知识串讲+热考题型+专题训练)-讲义 试卷 0 次下载
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题08+两角和与差的三角函数(10大考点,知识串讲+热考题型+专题训练)-讲义 试卷 0 次下载
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题09+二倍角的三角函数(6大考点,知识串讲+热考题型+专题训练)-讲义 试卷 0 次下载
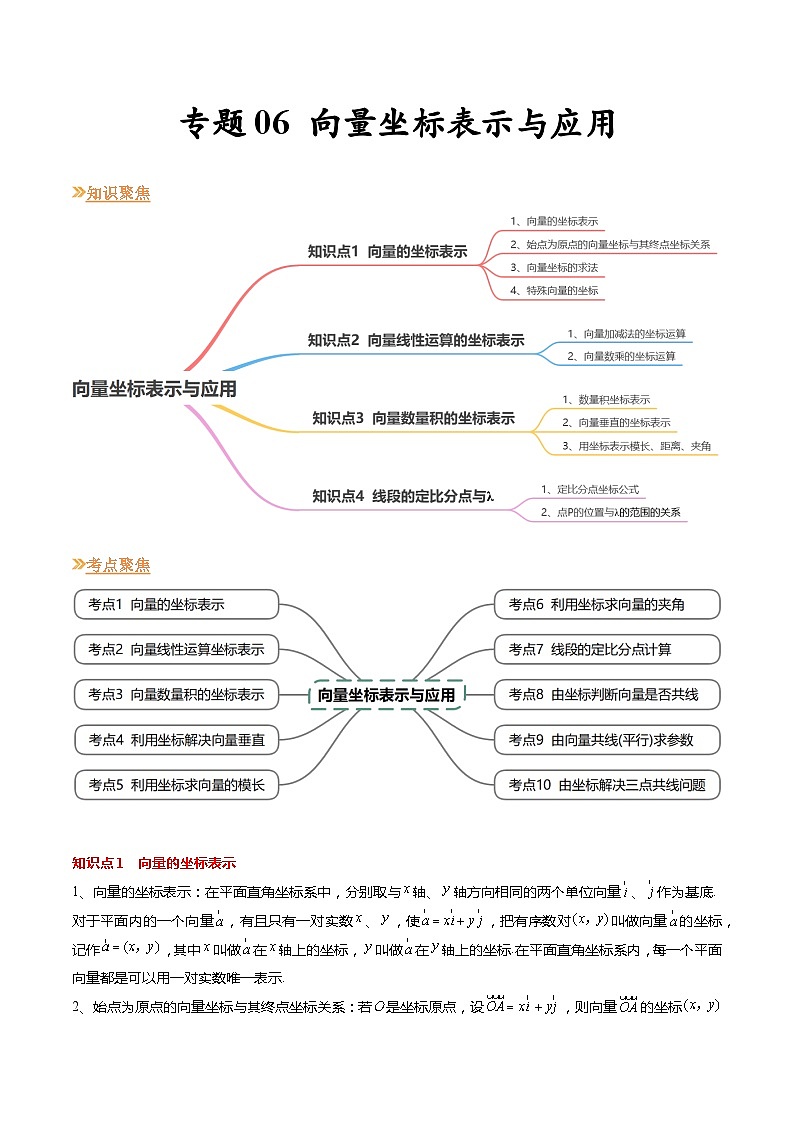
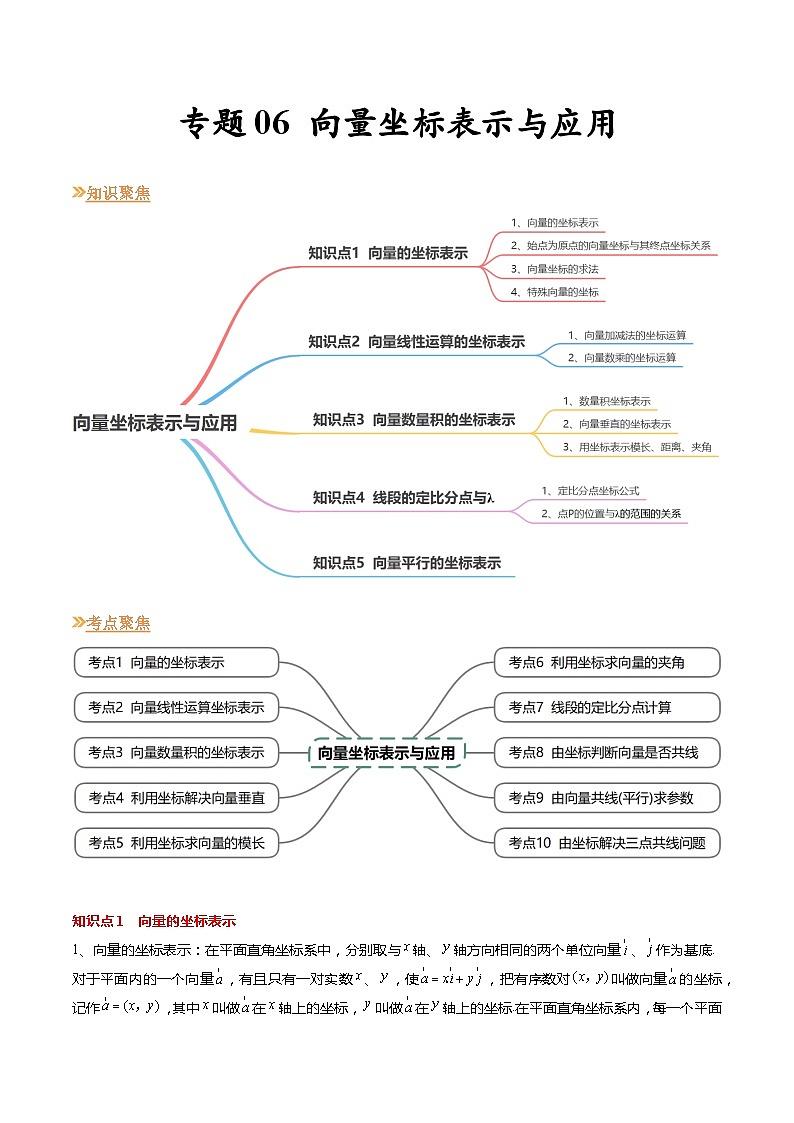
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题06+向量坐标表示与应用(10大考点,知识串讲+热考题型+专题训练)-讲义
展开知识聚焦
考点聚焦
知识点1 向量的坐标表示
1、向量的坐标表示:在平面直角坐标系中,分别取与轴、轴方向相同的两个单位向量、作为基底.对于平面内的一个向量,有且只有一对实数、,使,把有序数对叫做向量的坐标,记作,其中叫做在轴上的坐标,叫做在轴上的坐标.在平面直角坐标系内,每一个平面向量都是可以用一对实数唯一表示.
2、始点为原点的向量坐标与其终点坐标关系:若是坐标原点,设,则向量的坐标就是终点的坐标,即若,则点坐标为,反之亦成立.
3、向量坐标的求法:
①若向量的起点是坐标原点,则终点坐标即为向量的坐标;
②设、,则
4、特殊向量的坐标:.
【注意】
(1)在直角坐标平面内,以原点为起点的向量OA=a,点A的位置被向量a唯一确定,
此时点A的坐标与向量a的坐标统一为(x,y).
(2)由向量坐标的定义,知两向量相等的充要条件是它们的横、纵坐标对应相等,
即a=b⇔x1=x2且y1=y2,其中a=(x1,y1),b=(x2,y2).
(3)平面向量的坐标与该向量的起点、终点坐标有关;
应把向量坐标与点坐标区别开来,只有起点在原点时,向量坐标才与终点坐标相等.
(4)当向量确定以后,向量的坐标就是唯一确定的,因此向量在平移前后,其坐标不变.
知识点2 向量线性运算的坐标表示
1、向量加减法的坐标运算:已知,则,.
结论:两个向量和与差的坐标分别等于这两个向量相应坐标的和与差.
2、向量数乘的坐标运算:若,则;
结论:实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标。
知识点3 向量数量积的坐标表示
1、数量积坐标表示:若a=(x1,y1),b=(x2,y2),则a∙b=x1y1+x2y2
两个向量的数量积等于它们对应坐标乘积的和。
2、向量垂直的坐标表示:若两个向量垂直,则a⊥b⟺x1y1+x2y2=0
3、用坐标表示模长、距离、夹角
(1)向量的模公式:若a=(x1,y1),则a=x12+y12
(2)两点间的距离公式:若A(x1,y1),B(x2,y2),则AB=(x1-x2)2+(y1-y2)2
(3)向量的交角公式:设两个非零向量a=(x1,y1),b=(x2,y2),a与b的夹角为θ,
则csθ=a∙bab=x1x2+y1y2x12+y12x22+y22
知识点4 线段的定比分点与λ
设、是直线上的两点,是上不同于、的任一点,则一定存在实数,使,叫做点分所成的比.有三种情况:
(内分) (外分)() (外分) ()
(1)定比分点坐标公式:若点,,为实数,且,
则点坐标为,我们称为点分所成的比.
(2)点的位置与的范围的关系:
①当时,与同向共线,这时称点为的内分点;
②当()时,与反向共线,这时称点为的外分点.
知识点4 向量平行的坐标表示
坐标表示:一般地,设向量,,则
特别的,当且时,有,即两个向量的相应坐标成比例。
【注意事项】
(1)两个向量,平行的条件容易写错,该条件的正确记法为“交叉相乘,差为0”;
(2)当两个非零的共线向量的对应坐标同号或同为零时,同向;当两个非零的共线向量的对应坐标异号或同为零时,反向。
考点剖析
考点1 向量的坐标表示
【例1】(2023·江西·高一校联考期末)若点,则( )
A. B. C. D.
【答案】B
【解析】因为,所以,故选:B.
【变式1-1】(2023·高一课时练习)如图所示,为单位正交基,则向量,的坐标分别是( )
A., B., C., D.,
【答案】C
【解析】根据平面直角坐标系,可知,,
∴,,故选:C.
【变式1-2】(2023·新疆乌鲁木齐·高一校考期中)若,点的坐标为,则点的坐标为( )
A. B. C. D.
【答案】A
【解析】设,故,而,
故,故,故,故选:A.
【变式1-3】(2023·四川绵阳·高一南山中学实验学校校考期中)已知点,,向量,则向量( )
A. B. C. D.
【答案】A
【解析】设,则,
故,解得,所以,
又因为,所以.故选:A
【变式1-4】(2023·四川南充·高一统考期末)已知向量,将向量绕原点O沿逆时针方向旋转到的位置,则点的横坐标为( )
A. B. C.0 D.1
【答案】C
【解析】因为,所以向量与轴正方向的夹角为,
向量绕原点O沿逆时针方向旋转到的位置,则与轴正方向的夹角为,
此时点在轴上,点的横坐标为0,故选:C.
考点2 向量线性运算坐标表示
【例2】(2023·陕西西安·高一阶段练习)已知向量,,则( )
A. B. C. D.
【答案】D
【解析】因为,,所以.故选:D.
【变式2-1】(2023·西藏林芝·高一校考期末)已知向量,,则等于( )
A. B. C. D.
【答案】C
【解析】向量,,则.故选:C
【变式2-2】(2023·河南商丘·高一校考阶段练习)已知向量,则( )
A. B. C. D.
【答案】D
【解析】因为,所以.故选:D
【变式2-3】(2023·福建龙岩·高一校联考期中)若向量,,,则( )
A. B. C. D.
【答案】C
【解析】因为向量,,所以,故选:C.
【变式2-4】(2023·四川眉山·高一校考期中)已知向量满足,,,则( )
A.-1 B.0 C.1 D.
【答案】B
【解析】设,,又,,
所以,且,解得,,即,.
所以,
则,解得,故,故选:B.
考点3 向量数量积的坐标表示
【例3】(2023·河北沧州·高一校联考阶段练习)如图所示的图形中,每一个小正方形的边长均为1,则( )
A. B. C.0 D.4
【答案】D
【解析】如图,建立平面直角坐标系,每一个小正方形的边长均为1,
故,,
则.故选:D.
【变式3-1】(2023·广东阳江·高一广东两阳中学校考期末)已知,,若,则x等于( )
A.6 B.5 C.4 D.3
【答案】C
【解析】由题意,,,,,解得:.故选:C.
【变式3-2】(2023·江西宜春·高一校联考阶段练习)已知边长为2的菱形中,,点E是BC上一点,满足,则( )
A. B. C. D.
【答案】B
【解析】以为坐标原点,所在直线为轴,垂直于轴的直线为轴,建立平面直角坐标系,
则,设,
则,
因为,
所以,解得,故,
则.故选:B
【变式3-3】(2023·河北石家庄·高一校考期中)等腰梯形ABCD中,AB平行于CD,,,,P为腰AD所在直线上任意一点,则的最小值是( )
A. B.1 C. D.
【答案】C
【解析】等腰梯形ABCD中,作垂直于于点,作垂直于于点,
又,,,
则,,,,
则建立如图所示平面直角坐标系,
则,,,,
又P为腰AD所在直线上任意一点,
则设,,则点P的坐标为,
所以,,
又关于的二次函数的对称轴为,
则在上单调递减,
所以当,即点P和点D重合时,取得最小值.
故的最小值是.故选:C.
考点4 利用坐标解决向量垂直问题
【例4】(2023·云南昆明·高一校考期中)已知向量,,且,则( )
A.2 B.3 C.4 D.5
【答案】C
【解析】因为,所以,解得.故选:C.
【变式4-1】(2023·全国·高一随堂练习)已知向量,,若,则( )
A. B. C. D.
【答案】A
【解析】法一:用坐标表示向量
由题意可知,,
由得,,
整理得,,所以.则A对;
法二:因为向量,所以,
又,所以,
所以.故选:A.
【变式4-2】(2023·全国·高一随堂练习)已知,,,若,则 .
【答案】
【解析】由,,得,
又,则,解得.
【变式4-3】(2023·甘肃临夏·高一统考期末)已知点及平面向量,,.
(1)当点P在x轴上时,求实数m的值;
(2)当时,求实数k的值.
【答案】(1)4;(2)
【解析】(1),
因为点P在x轴上,所以,解得.
(2),,
又因为,
所以,解得.
考点5 利用坐标求向量的模长
【例5】(2023·全国·高一随堂练习)已知向量,则( )
A.10 B.5 C. D.
【答案】C
【解析】因为,所以,所以.故选:C
【变式5-1】(2023·北京顺义·高一牛栏山一中校考期中)已知向量,,则向量的模为 .
【答案】5
【解析】因为,,
又,所以,.
【变式5-2】(2023·云南昆明·高一校考阶段练习)设向量,,,则( )
A. B. C. D.10
【答案】C
【解析】,故,
又,,
故,解得.故选:C
【变式5-3】(2023·河南周口·高一统考期中)如图.在直角梯形中,,,,点P是腰上的动点,则的最小值为 .
【答案】4
【解析】由在直角梯形中.,
则,则以A为原点,为轴建立平面直角坐标系,
设,设,则,
故,
所以,故,
当且仅当即时取得等号,即的最小值为4.
考点6 利用坐标求向量的夹角
【例6】(2023·广东佛山·高一校联考阶段练习)已知向量,则与夹角的余弦值为 .
【答案】
【解析】由题意可得:,,
所以与夹角的余弦值.
【变式6-1】(2023·河北邢台·高一邢台市第二中学校考阶段练习)已知点,,向量,,则与的夹角的余弦值为( )
A. B. C. D.
【答案】A
【解析】因为点,,向量,,
所以,,
所以与的夹角的余弦值.故选:A
【变式6-2】(2023·贵州毕节·高一统考期末)已知向量,若,则( )
A. B. C. D.
【答案】D
【解析】因为,
所以,
又因为,所以,解得,
则,所以,
所以.故选:D
【变式6-3】(2023·上海·高一校考期末)若向量,,且与的夹角为锐角,则的取值范围为
【答案】
【解析】因为向量,,且与的夹角为锐角,所以,且与不共线,
由,得,解得,
若与共线,则,得,所以当时,与不共线,
综上,且,即的取值范围为.
考点7 利用坐标求向量的夹角
【例7】(2023·上海·高一控江中学校考期末)已知直角坐标平面上两点、,若满足,则点的坐标为 .
【答案】
【解析】设点的坐标为,
因为点,,所以,,
因为,所以,解得,
所以点的坐标为
【变式7-1】(2023·广东揭阳·高三统考期中)已知点,向量,,点是线段的三等分点,则点的坐标是( )
A. B. C.或 D.或
【答案】C
【解析】因为,,可得,
又因为点是线段的三等分点,
则或,
所以或,
即点的坐标为或.故选:C.
【变式7-2】(2023·贵州·高一校联考阶段练习)已知,,点分所成的比为,则与的值分别为( )
A. B. C. D.
【答案】D
【解析】∵,,,∴,,
∵分所成的比为,
∴,即,
∴有,解得.故选:D.
【变式7-3】(2023·山东枣庄·高一统考期末)(多选)已知点是的重心,点,,,点是上靠近点的三等分点,则( )
A. B. C. D.
【答案】AB
【解析】点是的重心,点,,,
设点,,A选项正确;
点是上靠近点的三等分点,则
设则即,解得,B选项正确;
因为,则,
即,C选项错误;
,D选项错误;故选:AB.
考点8 由坐标判断向量是否共线
【例8】(2023·全国·高一课时练习)(多选)下列向量组中,能作为平面内所有向量基底的是( )
A. B.
C. D.
【答案】ABC
【解析】能作为平面内的基底,则两向量与不平行,
A选项,,∴与不平行;
B选项,,∴与不平行;
C选项,,∴与不平行;
D选项,,∴.故选:ABC.
【变式8-1】(2023·浙江嘉兴·高一校考阶段练习)(多选)下列向量中与共线的是( )
A. B. C. D.
【答案】ACD
【解析】因为,所以与共线,因此选项A正确;
因为,所以与不共线,因此选项B不正确;
因为,所以与共线,因此选项C正确;
因为零向量与任何向量平行,因此选项D正确,故选:ACD
【变式8-2】(2023·贵州毕节·高一校考期中)已知向量,,则与向量共线的向量的坐标可以是( )
A. B. C. D.
【答案】A
【分析】根据条件求出向量的坐标,再结合向量共线的坐标公式逐项计算判断即可.
对选项A:因为,所以两向量共线,A正确;
对选项B:因为,所以两向量不共线,B错误;
对选项C:因为,所以两向量不共线,C错误;
对选项D:因为,所以两向量不共线,D错误;故选:A.
【变式8-4】(2023·北京平谷·高一统考期末)已知向量,,那么向量可以是( )
A. B. C. D.
【答案】A
【解析】向量,,则存在,使得
故只有向量符合,故选:A.
考点9 由向量共线(平行)求参数
【例9】(2023·黑龙江齐齐哈尔·高一齐齐哈尔中学校考期中)已知,,,若,则实数( )
A. B. C. D.
【答案】C
【解析】,,
由得,,解得,故选:C.
【变式9-1】(2023·河北邢台·高一邢台市第二中学校考阶段练习)向量,,,,若,则 .
【答案】6或
【解析】因为,所以设,
则,
若不共线,则,则,无实根,不符合题意;
则共线,因为向量,,
所以,解得或.
【变式9-2】(2023·全国·高一随堂练习)已知,,,当时,求实数x,y应满足的关系式.
【答案】
【解析】由已知可得,.
因为,所以,所以有,整理可得,.
【变式9-3】(2023上·湖南长沙·高二校考开学考试)平面给定三个向量,,
(1)若,求的值;
(2)若向量与向量共线,求实数k的值.
【答案】(1);(2)
【解析】(1)由题知,,所以,
又因为,所以,解得,所以.
(2)由题知,,
又因为与共线,所以,解得:.
考点10 由坐标解决三点共线问题
【例10】(2023·贵州安顺·高一统考期末)若三点、、共线,则实数的值为( )
A. B. C. D.
【答案】D
【解析】已知三点、、共线,则,,
由题意可知,所以,,解得.故选:D.
【变式10-1】(2023·江苏无锡·高一天一中学校考期末)已知点,,,若A,B,C三点共线,则的坐标为( )
A. B. C. D.
【答案】D
【解析】由题意可知
由于A,B,C三点共线,所以与共线,
所以,所以,故选:D
【变式10-2】(2023·河北邯郸·高一统考期中)已知向量,,,若B,C,D三点共线,则( )
A.-16 B.16 C. D.
【答案】A
【解析】由题意得,,
因为B,C,D三点共线,所以,则,得.故选:A.
【变式10-3】(2023·新疆·高一八一中学校考期末)在平面直角坐标系中,向量,,,若A,B,C三点共线,则的值为( )
A. B. C. D.
【答案】C
【解析】因为A,B,C三点共线,则,,
即,
则,解得.故选:C
过关检测
一、单选题
1.(2023·重庆·高一校考期中)已知,则的中点坐标是( )
A. B. C. D.
【答案】B
【解析】设的中点坐标是,
由三点共线可知,即,解得;
所以中点坐标为.故选:B
2.(2023·江苏淮安·高一统考期末)下列各组向量中,可以作为基底的是( )
A., B.,
C., D.,
【答案】D
【解析】只要两个向量不共线,即可作为基底向量
对于A,因为,,所以,则共线,故A不符合;
对于B,因为,,所以,则共线,故B不符合;
对于C,因为,,所以,则共线,故C不符合;
对于D,因为,,所以,
则不共线,故D符合;故选:D.
3.(2023·甘肃武威·高一天祝藏族自治县第一中学校考阶段练习)已知向量,,若,则( )
A. B. C. D.
【答案】B
【解析】因为向量,,,
所以,即,则.故选:B.
4.(2023·吉林长春·高一长春外国语学校校考阶段练习)已知向量,若,则( )
A. B. C. D.
【答案】C
【解析】向量,且,
故选:C
5.(2023·贵州安顺·高一统考期末)已知向量,则向量在向量上的投影向量( )
A. B. C. D.
【答案】D
【解析】因为,,
所以,,
所以向量在向量上的投影向量为.故选:D
6.(2023·河北保定·高一统考期中)已知、、三点共线,则( )
A. B. C. D.
【答案】C
【解析】因为、、,则,,
因为、、三点共线,则,所以,即.故选:C.
7.(2023·江苏常州·高一校联考期末)已知向量,,则与的夹角为( )
A. B. C. D.
【答案】A
【解析】因为,,
所以,,,
设与的夹角为,则,
又,所以.故选:A
8.(2023·四川成都·高一树德中学校考期末)已知对任意平面向量,把绕其起点沿逆时针方向旋转角得到向量,叫做把点绕点沿逆时针方向旋转角得到点.已知平面内点,把点绕点沿顺时针方向旋转后得到点,则点的坐标为( )
A. B. C. D.
【答案】D
【解析】设,则,将点绕点沿顺时针方向旋转,
即将点绕点沿逆时针方向旋转,
可得,
化简可得,,
又因为,
所以,解得,所以.故选:D
二、多选题
9.(2023·广西玉林·高一校联考期末)已知是单位向量,且,则( )
A.与垂直 B.
C.与的夹角为 D.在上投影向量的坐标为
【答案】AD
【解析】,因为是单位向量,
所以,所以,所以,故A正确;
因为,所以,故B错误;
因为,
设与的夹角为,所以,
所以与的夹角为,故错误;
在上的投影向量坐标为,所以D对.故选:AD.
10.(2023·云南大理·高一统考期末)已知向量,,则下列结论正确的是( )
A. B. C. D.
【答案】BD
【解析】因为向量,,
则,,
因此,A错误,B正确;
由,知C错误;
,D正确,故选:BD
11.(2023·广东东莞·高一校考阶段练习)(多选)已知平面向量,,,则下列说法正确的是( )
A.若,则 B.若,则
C.若,则向量在上的投影向量为 D.若,则向量与的夹角为锐角
【答案】AB
【解析】已知平面向量,,,
对于选项A,若,则,即,即选项A正确;
对于选项B,若,则,即,即选项B正确;
对于选项C,若,则,
则向量在上的投影向量为,即选项C错误;
对于选项D,当时,,
则当,向量与的夹角为锐角错误,即选项D错误,故选:AB.
12.(2023·广东中山·高一中山纪念中学校考阶段练习)在边长为2的正中,满足相交于点,则下列结论正确的是( )
A. B.
C. D.在上的投影向量为
【答案】AD
【解析】因为是边长为2的等边三角形,是上的点,且,
以为坐标原点,所在直线分别为轴、轴,建立平面直角坐标系如图:
则,
又因为,即为边上的一个靠近的三等分点,于是,
设,则,而,
由三点共线得,解得,即,因此是的中点,
因为,所以,A正确;
因为,,B错误;
显然,,
因此,C错误;
又因为,
所以在方向上的投影向量,D正确.故选:AD
三、填空题
13.(2023·上海闵行·高一校考阶段练习)已知向量,,则向量的单位向量是 .
【答案】
【解析】因为,,
所以,则,
所以向量的单位向量为.
14.(2023·河北石家庄·高一校考期中)已知向量,若与共线,则m的值为 .
【答案】
【解析】向量,则,
,
由向量与共线,得,解得,所以m的值为.
15.(2023·江苏泰州·高一统考期中)如图,在4×4的方格纸中,若起点和终点均在格点的向量,,满足,则 .
【答案】7
【解析】建立如图所示直角坐标系,设小方格的边长为单位长度1,
可得,同理可得,
,
将方程组中两式相加,可得.
16.(2023·湖北黄冈·高一校考阶段练习)设向量,,且,则 .
【答案】
【解析】由,得,
根据得,解得.
四、解答题
17.(2023·河南省直辖县级单位·高一济源市第四中学校考阶段练习)已知向量,,
(1)分别求,的坐标;
(2)若向量,且与向量平行,求实数k的值.
【答案】(1),;(2).
【解析】(1)依题意,,
.
(2)由(1)知,而,
由与向量平行,得,解得:,
所以实数k的值是.
18.(2023·云南怒江·高一校考阶段练习)已知,.
(1)已知,,在所给直角坐标系中标出A,B两点的位置;
(2)求;
(3)求.
【答案】(1)答案见解析;(2);(3).
【解析】(1)由,,得,
所以,,在直角坐标系中A,B两点的位置如下:
(2),,,,
.
(3),.
19.(2023·天津武清·高一校考阶段练习)已知向量,
(1)向量在向量上的投影向量的坐标;
(2)求
(3)若与垂直,求实数的值.
【答案】(1);(2)8;(3)19
【解析】(1).
(2)因为,所以.
(3),
,
因为与垂直,所以,
得,解得,
即当时,与垂直.
20.(2023·广东佛山·高一校考阶段练习)已知,.
(1)若,,且、、三点共线,求的值
(2)当为何值时,有与垂直
【答案】(1);(2)
【解析】(1),,
,,
,,三点共线,与共线,
,解得;
(2),,
与垂直,,解得.
21.(2023·四川成都·高一树德中学校考期末)已知,,,.
(1)为何值时,点在轴上?
(2)若与的夹角是钝角,求的取值范围.
【答案】(1);(2)
【解析】(1)由题意知:,,
所以,.
因为点在轴上,所以,解得.
(2)因为,所以与不共线.
又与的夹角是钝角,所以只需,
即,解得.
22.(2023·高一单元测试)已知坐标平面内三点,,.
(1)若,,,可以构成平行四边形,且点在第一象限,求点的坐标;
(2)若是线段上一动点,求的取值范围.
【答案】(1);(2)
【解析】(1)设(),依题意可得,
又,,,
所以,,
所以,解得,即.
(2)设,,则,
所以,则,
所以,
因为,所以当时取最小值,
当时取最大值,
所以的取值范围为.
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题11+余弦定理(6大考点,知识串讲+热考题型+专题训练)-讲义: 这是一份【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题11+余弦定理(6大考点,知识串讲+热考题型+专题训练)-讲义,文件包含寒假作业苏教版2019高中数学高一寒假提升训练专题11余弦定理6大考点知识串讲+热考题型+专题训练原卷版docx、寒假作业苏教版2019高中数学高一寒假提升训练专题11余弦定理6大考点知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题07+向量的应用(8大考点,知识串讲+热考题型+专题训练)-讲义: 这是一份【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题07+向量的应用(8大考点,知识串讲+热考题型+专题训练)-讲义,文件包含寒假作业苏教版2019高中数学高一寒假提升训练专题07向量的应用8大考点知识串讲+热考题型+专题训练原卷版docx、寒假作业苏教版2019高中数学高一寒假提升训练专题07向量的应用8大考点知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题05+平面向量基本定理(6大考点,知识串讲+热考题型+专题训练)-讲义: 这是一份【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题05+平面向量基本定理(6大考点,知识串讲+热考题型+专题训练)-讲义,文件包含寒假作业苏教版2019高中数学高一寒假提升训练专题05平面向量基本定理6大考点知识串讲+热考题型+专题训练原卷版docx、寒假作业苏教版2019高中数学高一寒假提升训练专题05平面向量基本定理6大考点知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。