【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题02 向量的加减法（6大考点，知识串讲+热考题型+专题训练）-讲义

这是一份【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题02 向量的加减法（6大考点，知识串讲+热考题型+专题训练）-讲义，文件包含寒假作业苏教版2019高中数学高一寒假提升训练专题02向量的加减法6大考点知识串讲+热考题型+专题训练原卷版docx、寒假作业苏教版2019高中数学高一寒假提升训练专题02向量的加减法6大考点知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源，其中试卷共28页， 欢迎下载使用。

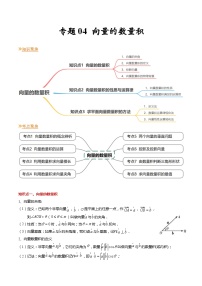
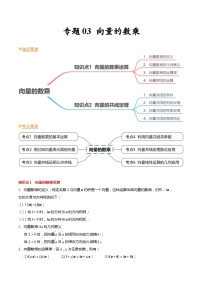
知识聚焦
考点聚焦
知识点1 向量的加法运算
1、向量加法的定义：求两个向量和的运算，叫做向量的加法。
2、向量加法的三角形法则：已知非零向量a，b，在平面内任取一点A，作AB＝a，BC＝b，再作向量AC，
向量AC叫做a与b的和，记作a＋b，即a＋b＝AB＋BC＝AC
3、向量加法的平行四边形法则：已知不共线的两个向量a，b，在平面内任取一点O，
以同一点O为起点的两个已知向量a，b为邻边作▱OACB，对角线OC就是a与b的和
【规定】零向量与任一向量a的和都有a＋0eq \a\vs4\al(＝)0＋a＝eq \a\vs4\al(a).
【注意】（1）在使用向量加法的三角形法则时，要注意“首尾相接”，即第一个向量的终点与第二个向量的起点重合，则以第一个向量的起点为起点，并以第二个向量的终点为终点的向量即两向量的和；
（2）平行四边形法则的应用前提是“共起点”，即两个向量是从同一点出发的不共线向量．
4、向量加法的运算律
结合律：a＋b＝b＋a 交换律：(a＋b)＋c＝a＋(b＋c)
知识点2 向量的减法
1、相反向量：与a长度相等、方向相反的向量，叫做a的相反向量，记作－a.
（1）规定：零向量的相反向量仍是仍是零向量；
（2）－(－a)＝a；
（3）a＋(－a)＝(－a)＋a＝0；
（4）若a与b互为相反向量，则a＝－b，b＝－a，a＋b＝0.
【注意】相反向量与相等向量一样，从“长度”和“方向”两方面定义，相反向量必为平行向量．
2、向量的减法
（1）定义：a－b＝a＋(－b)，即减去一个向量相当于加上这个向量的相反向量.
（2）几何意义：以O为起点，作向量eq \(OA,\s\up7(―→))＝a，eq \(OB,\s\up7(―→))＝b，则eq \(BA,\s\up7(―→)) ＝a－b，
如图所示，即a－b可表示从向量b的终点指向向量a的终点的向量．
【注意】在用三角形法则作向量减法时，只要记住“连接向量终点，箭头指向被减向量”即可．
考点剖析
考点1 向量的加减法法则及应用
【例1】（2023·全国·高一随堂练习）如图，已知向量、，用向量加法的平行四边形法则作出向量．
（1） （2）
【变式1-1】（2023·全国·高一随堂练习）如图，已知向量，，不共线，求作向量．
【变式1-2】（2023·海南·高一校考期中）如图，在正六边形ABCDEF中，（ ）
A． B． C． D．
【变式1-3】（2022·高一校考课时练习）如图，在矩形ABCD中，O为AC与BD的交点，则（ ）
A． B． C． D．
【变式1-4】（2023·云南迪庆·高一统考期末）四边形是梯形，，则等于（ ）
A． B． C． D．
考点2 向量的减法法则及应用
【例2】（2022·高一课时练习）如图，已知向量，，求作向量．
【变式2-1】（2023·山东枣庄·高一校考阶段练习）如图，点O是平行四边形ABCD两条对角线的交点，则下列等式一定成立的是（ ）
A． B． C． D．
【变式2-2】（2023·河南驻马店·高一统考期末）已知矩形的对角线相交于点，则（ ）
A． B． C． D．
【变式2-3】（2023·吉林长春·高一东北师大附中校考阶段练习）如图所示，、、分别是的边、、的中点，则（ ）
A． B． C． D．
【变式2-4】（2022·高一课前预习）化简下列式子：
（1）；
（2）；
考点3 向量加减法运算化简
【例3】（2023·广东东莞·高一厚街中学校考阶段练习）化简向量等于（ ）
A． B． C． D．
【变式3-1】（2023·河南·高一济源第一中学校考阶段练习）在平面四边形中，下列表达式化简结果与相等的是（ ）
A． B． C． D．
【变式3-2】（2023·全国·高一随堂练习）下列各式中，化简后不是零向量的是（ ）
A． B．
C． D．
【变式3-3】（2023·河南新乡·高一校考阶段练习）（多选）化简以下各式，结果为的有（ ）
A． B．
C． D．
【变式3-4】（2023·全国·高一课时练习）（化简下列各式：
（1）；
（2）．
考点4 利用向量加减法证明等式
【例4】（2023·高一单元测试）如图所示，P，Q是的边BC上两点，且.求证：.
【变式4-1】（2022·高一课时练习）如图所示，点分别为的三边的中点.
求证：
（1）；
（2）.
【变式4-2】（2022·高一课时练习）如图所示，是平行四边形的对角线的交点，设，，，求证：.
【变式4-3】（2023·高一课时练习）已知平行四边形ABCD的两条对角线AC与BD交于点E，O是任意一点，求证：．
考点5 向量加减法在几何中的应用
【例5】（2023·河南驻马店·高一校联考期中）在中，，则是（ ）
A．等边三角形 B．直角三角形 C．钝角三角形 D．等腰直角三角形
【变式5-1】（2023·安徽合肥·高一合肥一中校考阶段练习）若在△ABC中，，，且，，则△ABC的形状是（ ）
A．正三角形 B．锐角三角形 C．斜三角形 D．等腰直角三角形
【变式5-2】（2023·云南西双版纳·高一校考期中）在四边形中，若，且，则（ ）
A．在四边形是矩形 B．在四边形是菱形
C．在四边形是正方形 D．在四边形是平行四边形
【变式5-3】（2023·陕西咸阳·高一校考期中）已知是四边形所在平面上任一点，且．则四边形一定为（ ）
A．菱形 B．梯形 C．平行四边形 D．矩形
【变式5-4】（2023·浙江温州·高一统考期末）在四边形ABCD中，已知，则四边形ABCD为（ ）
A．矩形 B．菱形 C．正方形 D．平行四边形
考点6 向量加减法在实际中的应用
【例6】（2023·高一课时练习）人骑自行车的速度为，风速为，则逆风行驶的速度为（ ）
A． B． C． D．
【变式6-1】（2023·陕西榆林·高一统考期末）若向量表示“向东航行”，向量表示“向北航行”，则向量表示（ ）
A．向东北方向航行 B．向北偏东方向航行
C．向正北方向航行 D．向正东方向航行
【变式6-2】（2023·云南文山·高二校考阶段练习）如图，一个人骑自行车由A地出发到达B地，然后由B地出发到达C地，则这个人由A地到C地位移的结果为（ ）
A． B． C． D．
【变式6-3】（2023·江苏常州·高一常州市北郊高级中学校考阶段练习）某人在静水中游泳的速度为，河水自西向东的流速为，此人朝正南方向游去，那么他的实际前进方向与水流方向的夹角为（ ）
A． B． C． D．
【变式6-4】（2022·高一课时练习）在静水中船的速度是，水流的速度是.如果船从岸边出发，沿垂直于水流的航线到达对岸，那么船行进方向应指向何处？实际航速为多少？
过关检测
一、单选题
1．（2023·重庆万州·高一校考阶段练习）下列各式中不能化简为的是（ ）
A．B．
C．D．
2．（2023·全国·高一专题练习）（ ）
A．B．C．D．
3．（2023·河北邢台·高一邢台市第二中学校考阶段练习）在平面四边形ABCD中，E为线段CD上任一点，则（ ）
A．B．C．D．
4．（2023·天津红桥·高一统考期末）化简：（ ）
A．B．C．D．
5．（2023·新疆·高一校考期末）在矩形中，等于（ ）
A．B．C．D．
6．（2023·全国·高一课时练习）在四边形中，，则一定有（ ）
A．四边形是矩形B．四边形是菱形
C．四边形是正方形D．四边形是平行四边形
7．（2023·江西赣州·高一校联考期中）化简以下各式:①；②；③；④，结果为零向量的个数是（ ）
A．1B．2C．3D．4
8．（2023·北京通州·高一统考期末）对于任意两个向量和，下列命题中正确的是（ ）
A．B．
C．D．
二、多选题
9．（2023·全国·高一课时练习）下列各式中，结果为零向量的是（ ）
A．B．
C．D．
10．（2023·安徽铜陵·高一铜陵一中校考阶段练习）下列能化简为的是（ ）
A．B．
C．D．
11．（2023·全国·高一专题练习）在平面四边形ABCD中，E，F分别为AD，BC的中点，则下列向量与相等的是（ ）
A．B．C．D．
12．（2023·内蒙古包头·高一统考期末）已知，，，四点不共线，下列等式能判断为平行四边形的是（ ）
A．B．（为平面内任意一点）
C．D．（为平面内任意一点）
三、填空题
13．（2023·高一课时练习）若向量表示向东走千米，表示向南走千米，则向量表示 ．
14．（2023·全国·高一课时练习）化简：
（1） ； （2） ；
（3） ； （4） ．
15．（2023·河南开封·高一河南省杞县高中校考期中）已知非零向量满足，且，则 .
16．（2023·高一单元测试）任给两个向量和，则下列式子恒成立的有 ．
① ②
③ ④
四、解答题
17．（2023·江西吉安·高二宁冈中学校考期末）作出以下图形
（1）如图1，已知向量 不共线，作向量.
（2）如图2，已知向量，求作向量.
18．（2023·河北石家庄·高一校考阶段练习）化简下列各式：
（1）；
（2）
19．（2023·新疆·高一校考期中）化简下列各向量的表达式：
（1）；
（2）；
（3）；
20．（2023·湖北·高一校联考阶段练习）如图，E，F，G，H分别是梯形ABCD的边AB，BC，CD，DA的中点，，，，，用，表示下列各式．
（1）；
（2）．
21．（2023·安徽马鞍山·高一马鞍山二中校考阶段练习）如图所示，已知正方形ABCD的边长为1，，，，求：
（1）；
（2）．
22．（2023·河南南阳·高一统考阶段练习）如图所示，在平行四边形中，，分别为边和的中点，为与的交点．
（1）若，则四边形是什么特殊的平行四边形？说明理由．
（2）化简，并在图中作出表示该化简结果的向量．