- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题02 常用逻辑用语(10大考点,知识串讲+热考题型+专题训练)- 试卷 0 次下载
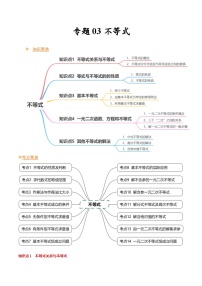
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题03 不等式(14大考点,知识串讲+热考题型+专题训练)- 试卷 0 次下载
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题05 函数的基本性质(12大考点,知识串讲+热考题型+专题训练)- 试卷 0 次下载
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题06 幂指对函数的图象与性质(10大考点,知识串讲+热考题型+专题训练)- 试卷 0 次下载
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题07 三角函数的概念与诱导公式(12大考点,知识串讲+热考题型+专题训练)- 试卷 0 次下载
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题04 函数的概念及表示(10大考点,知识串讲+热考题型+专题训练)-
展开知识聚焦
考点聚焦
知识点1 函数的定义及相关概念
1、函数的定义:设A,B是两个非空数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,
称f:A→B为从集合A到集合B的一个函数,记作:y=f(x),x∈A
【注意】函数的本质含义:定义域内的任意一个x值,必须有且仅有唯一的y值与之对应。
(1)特殊性:定义的集合A,B必须是两个非空数集;
(2)任意性:A中任意一个数都要考虑到;
(3)唯一性:每一个自变量都在B中有唯一的值与之对应;
(4)方向性:A→B
2、函数的有关概念
(1)函数的定义域、值域:在函数y=f(x),x∈A中,x叫做自变量,x的取值范围A叫做函数的定义域;
与x的值相对应的y值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的值域.
(2)函数的三要素:定义域、对应关系和值域.
(3)函数的表示法:表示函数的常用方法有解析法、图象法和列表法.
3、同一个函数:两个函数定义域相同,对应关系相同,则称为同一个函数。
知识点2 函数定义域的求法
函数的定义域是指使函数有意义的自变量的取值范围
1、具体函数的定义域求法
(1)分式的分母不能为零.
(2)偶次方根的被开方数的被开方数必须大于等于零,即中
奇次方根的被开方数取全体实数,即中,.
(3)零次幂的底数不能为零,即中.
(4)若函数是一些简单函数通过四则运算复合而成的,那么它的定义域是各个简单函数定义域的交集。
【注意】定义域用集合或区间表示,若用区间表示熟记,不能用“或”连接,而应用并集符号“∪”连接。
2、抽象函数与复合函数定义域的求法
复合函数的定义域是指的范围,而不是的范围。
(1)已知的定义域为,求的定义域,其实质是的取值范围(值域)为,求的取值范围;
(2)已知的定义域为,求的定义域,其实质是已知中的的取值范围为,求出的范围(值域),即的定义域.
(3)已知的定义域,求的定义域,要先按(2)求出的定义域,即的取值范围,再根据的取值范围求出的范围。
知识点3 函数解析式的求法
1、待定系数法:若已知函数的类型(如一次函数、二次函数等),可用待定系数法.
(1)确定所有函数问题含待定系数的一般解析式;
(2)根据恒等条件,列出一组含有待定系数的方程;
(3)解方程或消去待定系数,从而使问题得到解决。
2、换元法:主要用于解决已知的解析式,求函数的解析式的问题
(1)先令,注意分析的取值范围;
(2)反解出x,即用含的代数式表示x;
(3)将中的x度替换为的表示,可求得的解析式,从而求得。
3、配凑法:由已知条件,可将改写成关于的表达式,
然后以x替代g(x),便得的解析式.
4、方程组法:主要解决已知与、、……的方程,求解析式。
例如:若条件是关于与的条件(或者与)的条件,
可把代为(或者把代为)得到第二个式子,与原式联立方程组,求出
知识点4 分段函数
1、分段函数的定义:在函数定义域内,对于自变量x的不同取值范围,有着不同的对应关系的函数.
2、分段函数的性质:(1)分段函数是一个函数,其定义域、值域分别是各段函数的定义域、值域的并集;
各段函数的定义域的交集是空集.
(2)作分段函数图象时,应分别作出每一段的图象.
3、求分段函数的函数值
(1)分段函数求值,一定要注意所给自变量的值所在的范围,代入相应的解析式求得.
(2)若题中含有多层“f”的问题,要按照“由里到外”的顺序,层层处理.
(3)已知函数值求相应的自变量值时,应在各段中分别求解.
考点剖析
考点1 函数定义的理解与辨析
【例1】(2023·全国·高一专题练习)某校有一班级,设变量x是该班同学的姓名,变量y是该班同学的学号,变量z是该班同学的身高,变量w是该班同学的数学考试成绩,则下列选项中正确的是( )
A.y是x的函数 B.w是y的函数 C.w是z的函数 D.w是x的函数
【答案】B
【解析】对于AD,由于同学姓名非数字,故AD错误;
对于B,任意一个学号都对应一位确定的同学,
则该同学的数学成绩也是唯一确定的,故B正确;
对于C,假设班级中有两位身高相同的同学,
则这个身高可能对应两个不同同学的数学成绩,故C错误;故选:B.
【变式1-1】(2023秋·安徽阜阳·高一校考阶段练习)(多选)下列说法正确的是( )
A.函数值域中的每一个数在定义域中都有数与之对应
B.函数的定义域和值域一定是无限集合
C.对于任何一个函数,如果x不同,那么y的值也不同
D.表示当时,函数的值,这是一个常量
【答案】AD
【解析】对A,函数是一个数集与另一个数集间的特殊对应关系,
所给出的对应是否可以确定为y是x的函数,
主要是看其是否满足函数的三个特征,A正确;
对B,函数的定义域和值域不一定是无限集合,也可以是有限集,但一定不是空集,
如函数,定义域为,值域为,B错误;
对C,当x不同时,函数y的值可能相同,如函数,当和时,y都为1,C错误;
对D,表示当时,函数的值是一个常量,D正确.故选:AD
【变式1-2】(2023·全国·高一专题练习)下列对应是从集合A到集合B的函数的是( )
A. B.
C. D.
【答案】A
【解析】对于A选项,对集合A中的任意一个数x,集合B中都有唯一的数y与之对应,是函数;
对于B选项,时,,有两个y与之对应,不是函数;
对于C选项,当时,不存在,不是函数;
对于D选项,集合A中的元素0在集合B中没有对应元素,不是函数.故选:A
【变式1-3】(2023·全国·高一专题练习)(多选)已知集合=,集合=,下列能表示从集合到集合的函数关系的是( )
A. B. C. D.
【答案】BD
【解析】对于选项A:显然当时,在集合中,没有与之对应的实数,
故不表示从集合到集合的函数关系,所以本选项不符合题意;
对于选项B:当时,任意一个,在集合中,都有唯一与之对应的实数,
故表示从集合到集合的函数关系,所以本选项符合题意;
对于选项C:显然当时,在集合中有两个数与之对应,
故不表示从集合到集合的函数关系,所以本选项不符合题意;
对于选项D:当时,任意一个,在集合中,都有唯一与之对应的实数,
故表示从集合到集合的函数关系,所以本选项符合题意,故选:BD
【变式1-4】(2022秋·高一单元测试)(多选)下列图象中,能表示函数的图象的是( )
A. B. C. D.
【答案】ABC
【解析】对于选项ABC,当取一个值时,有唯一值与之对应,符合函数定义,故ABC正确;
D选项,当取一个值时,有两个值与之对应,不符合函数的定义,故D错误.故选:ABC
考点2 同一个函数的判断
【例2】(2022秋·江苏苏州·高一校考阶段练习)以下四组函数中,表示同一个函数的是( )
A.与 B.与
C.与 D.与
【答案】B
【解析】从定义域,对应关系,值域是否相同,逐项判断即可.
对于A:的值域为,的值域为,所以A错误;
对于B:的定义域需满足,即为,
的定义域满足,即为,且,
所以和是同一个函数,B正确;
对于C:的定义域为,的定义域为,所以C错误;
对于D:的定义域满足,即为,
的定义域需满足,即为,所以D错误,故选:B
【变式2-1】(2023秋·云南曲靖·高一校考阶段练习)下列各组中的两个函数为同一函数的是( )
A. B.
C. D.
【答案】C
【解析】A项:的定义域不包括,两个函数的定义域不同,所以是不同函数;
B项:,即对应关系不同;
C项:定义域都是实数集,对应关系都相同,是同一函数;
D项:的定义域不包括,两个函数的定义域不同,所以是不同函数.故选: C.
【变式2-2】(2023秋·河南郑州·高一校考阶段练习)下列各组函数表示相同函数的是( )
A.和 B.和
C.和 D.和
【答案】C
【解析】根据函数的定义域及对应法则判断是否为同一函数即可.
对于A中,函数的定义域为,函数的定义域为,
两个函数的定义域不同,所以表示不同的函数;
对于B中,函数的定义域为,函数的定义域为,
两个函数的定义域不同,所以表示不同的函数;
对于C中,函数与的定义域和对应法则都相同,
所以表示相同的函数;
对于D中,函数的定义域为,函数的定义域为,
两个函数的定义域不同,所以表示不同的函数.故选:C
【变式2-3】(2023秋·宁夏银川·高一校考期中)(多选)在下列四组函数中,与不表示同一函数的是( )
A., B.,
C., D.,
【答案】ABC
【解析】对A,,与定义域不同;
对B,,与定义域不同;
对C,,与定义域不同;
对D,,则与为同一函数.故选:ABC
考点3 求具体函数的定义域
【例3】(2023秋·宁夏银川·高一校考期中)函数的定义域为( )
A. B. C. D.
【答案】C
【解析】要使函数有意义,则解得,且,
故函数的定义域为.故选:C
【变式3-1】(2023·全国·高一专题练习)函数的定义域为( )
A. B. C. D.
【答案】C
【解析】要使函数有意义,
则,解得且,
因此,函数的定义域为.故选:C.
【变式3-2】(2023秋·广东梅州·高一校考期中)函数 的定义域是 .
【答案】
【解析】由题意,在中,
,解得:且,
故答案为:.
【变式3-3】(2023秋·黑龙江哈尔滨·高一校考阶段练习)函数的定义域为 .
【答案】
【解析】依题意可得,解得且.
所以函数的定义域为.
考点4 求抽象函数的定义域
【例4】(2023·江苏·高一专题练习)已知函数的定义域为,则函数的定义域为( )
A. B. C. D.
【答案】C
【解析】对于函数可知:,所以,即的定义域为,
对于函数可知:,解得,
故的定义域是.故选:C.
【变式4-1】(2023秋·河北唐山·高一校考阶段练习)已知函数的定义域为,则函数的定义域为 .
【答案】
【解析】对于,令,则,
所以,即的定义域为.
故答案为:
【变式4-2】(2023秋·江苏无锡·高一校考阶段练习)已知函数的定义域为,则函数的定义域为 .
【答案】
【解析】函数的定义域为,
令,解得,即,
所以函数的定义域为.
故答案为:.
【变式4-3】(2023秋·重庆·高一校考阶段练习)已知函数的定义域为,则函数的定义域是( )
A. B. C. D.
【答案】D
【解析】由题意得,解得,
又,解得,故函数的定义域是 .故选:D.
考点5 由函数定义域求参数
【例5】(2023·全国·高一专题练习)函数在上有意义,则实数a的取值范围为 .
【答案】
【解析】由题意函数在上有意义,
即在上恒成立,即在上恒成立,
令,则,解得,
故实数a的取值范围为,
【变式5-1】(2023秋·山东德州·高一校考阶段练习)若函数的定义域为,则实数的取值范围为 .
【答案】
【解析】由题意得,在R上恒成立,
当时,,成立;
当时,,即,解得;
综上所述,.
【变式5-2】(2023秋·内蒙古赤峰·高一校考阶段练习)若函数的定义域为,则实数的取值集合是 .(用区间表示)
【答案】
【解析】若函数的定义域为,则对任意实数恒成立,
①当时,恒成立,符合题意;
②当时,若,
则需满足,解得:;
综上所述:.即.
【变式5-3】(2023秋·福建漳州·高一校考阶段练习)已知函数的定义域为R,则实数a的取值范围为( )
A. B.或 C. D.或
【答案】C
【解析】由函数的定义域为R,得,恒成立.
当时,恒成立;
当时,,解得.
综上所述,实数a的取值范围为.故选:C.
考点6 待定系数法求解析式
【例6】(2023秋·福建厦门·高一校考阶段练习)已知是一次函数,且,则 .
【答案】
【解析】设,因为,
则,,故,,所以.
【变式6-1】(2023·全国·高一专题练习)设为一次函数且,求.
【答案】或
【解析】设,则.
又,∴,
即,解得或.
∴或.
∴或.
【变式6-2】(2023秋·浙江嘉兴·高一校考阶段练习)已知函数是一次函数,且,则( )
A.11 B.9 C.7 D.5
【答案】A
【解析】设,
则,
整理得,
所以,解,
所以,所以.故选:A
【变式6-3】(2023·全国·高一专题练习)已知二次函数满足,且的最大值是8,则此二次函数的解析式为( )
A. B. C. D.
【答案】A
【解析】根据题意,由得:图象的对称轴为直线,
设二次函数为,
因的最大值是8,所以,当时, ,
即二次函数,
由得:,解得:,
则二次函数,故选:A.
【变式6-4】(2023秋·福建南平·高一校考阶段练习)设二次函数满足,且,求的解析式.
【答案】
【解析】设二次函数为,
因为,所以,所以,
又因为,
即,
所以,解得:,
所以函数解析式为.
考点7 换元法/配凑法求解析式
【例7】(2023秋·福建漳州·高一校考阶段练习)已知,则( )
A. B. C. D.
【答案】B
【解析】令,,则,,
所以,
所以的解析式为:,故选:B.
【变式7-1】(2023·全国·高一专题练习)已知函数,则的解析式为( )
A. B.
C. D.
【答案】D
【解析】令,可得.
所以,
因此的解析式为.故选:D.
【变式7-2】(2023秋·安徽阜阳·高一校考阶段练习)已知函数,则函数的解析式是( )
A., B.,
C., D.,
【答案】B
【解析】,且,
所以,.故选:B.
【变式7-3】(2023·全国·高一专题练习)已知函数,则的解析式为( )
A. B. C. D.
【答案】D
【解析】因为,
所以.故选:D.
【变式7-4】(2023·全国·高一专题练习)已知,则函数 ,= .
【答案】 11
【解析】令,则,
所以,所以,
所以.
考点8 方程组法求解析式
【例8】(2023秋·全国·高一专题练习)已知函数的定义域为R,对任意均满足:则函数解析式为( )
A. B. C. D.
【答案】A
【解析】由,可得①,
又②,①+②得:,解得,故选:A.
【变式8-1】(2023秋·浙江温州·高一校考阶段练习)已知函数对定义域内的任意实数满足,则 .
【答案】
【解析】因为,取,则,即,
两式相加可得,所以.
【变式8-2】(2023秋·全国·高一专题练习)已知,求函数的解析式.
【答案】
【解析】①,
以替换,得②,
得:,
所以.
【变式8-3】(2023秋·江苏苏州·高一校考阶段练习)已知满足,则解析式为 .
【答案】
【解析】由 ①
用代可得, ②
由①②可得:
考点9 分段函数求值与求参
【例9】(2023·全国·高一专题练习)已知函数,那么的值是( )
A.8 B.7 C.6 D.5
【答案】A
【解析】因为函数,所以.故选:A.
【变式9-1】(2023·全国·高一专题练习)已知函数,,当时,,的值分别为( )
A.1,0 B.0,0 C.1,1 D.0,1
【答案】A
【解析】当x为有理数时,,,
,
当x为无理数时,,,
,,故选:D
【变式9-2】(2023秋·广东佛山·高一佛山一中校考开学考试)函数可用表示,例如,当时,.若函数.则的值为 .
【答案】
【解析】,
.故答案为:.
【变式9-3】(2023·全国·高一专题练习)已知函数,若,实数( )
A.1 B.2 C.3 D.4
【答案】C
【解析】因为,所以,
所以,解得.故选:C
【变式9-4】(2023秋·广东东莞·高一校联考阶段练习)已知函数,且.
(1)求;
(2)若,求实数的值.
【答案】(1)-2;(2).
【解析】(1),由于,故,解得
故,所以.
(2)当时,,解得,舍去;
当时,,解得或-1,
其中不符合题意,舍去;
综上所述,.
考点10 解分段函数不等式
【例10】(2023·江苏·高一专题练习)已知,若,则的取值范围为( )
A. B. C. D.
【答案】C
【解析】已知,
当时, ,由得,;
当时,,由得,解得,此时不等式无解;
当时,,由,得,解得,此时不等式无解.
综上所述,的取值范围是.故选:C.
【变式10-1】(2023秋·山东德州·高一校考阶段练习)已知函数,令,则不等式的解集是 .
【答案】
【解析】由题知,当时,即,解得:,
此时,;
当,即,解得:或,此时,;
.
由,得:或或,解得:,
故答案为:.
【变式10-2】(2023·全国·高一专题练习)已知函数则使成立的的值组成的集合为 .
【答案】
【解析】由题意可得或
由解得;
由解得.
综上所述,使成立的的值组成的集合为.
【变式10-3】(2023·全国·高一专题练习)已知,满足,则的取值范围是 .
【答案】
【解析】若,则,故,
由可得,
当,则,故,
由可得,
当时,则不符合要求,
综上可知:的取值范围为
【变式10-4】(2023·全国·高一专题练习)设函数,若,则的取值范围是 .
【答案】
【解析】(i)当,即时,,,
由得,即,
因为,所以恒成立,所以;
(ii)当,即时,,,
由得,即,
即恒成立,所以;
(iii)当,即时,,,
由得,即,所以,
综上所述:的取值范围是.
过关检测
1.(2023·江苏·高一专题练习)函数的定义域为( )
A. B. C. D.
【答案】C
【解析】由题意可得:,解得且,
所以函数的定义域为.故选:C.
2.(2023秋·江苏南京·高一校考阶段练习)若,则下列等式中组成立的是( )
A. B. C. D.
【答案】A
【解析】,则,
故即.故选:A.
3.(2023秋·山东青岛·高一校考阶段练习)已知函数的定义域为,则函数的定义域为( )
A.或 B.或
C.或 D.
【答案】A
【解析】由已知可得,,解得,或.故选:A.
4.(2023秋·全国·高一专题练习)已知函数的定义域是,则函数的定义域( )
A. B. C. D.
【答案】D
【解析】因为函数的定义域是,所以,
令,解得,所以函数的定义域为.故选:D
5.(2023秋·江苏徐州·高一校考阶段练习)已知函数则( )
A.1 B.2 C.4 D.5
【答案】B
【解析】由题意得.故选:B.
6.(2023·全国·高一专题练习)设,则不等式的解集是( )
A. B. C. D.
【答案】A
【解析】当时,由得:,解得:或,;
当时,由得:,解得:,;
不等式的解集是.故选:A.
7.(2023秋·吉林长春·高一校考阶段练习)(多选)下列是函数图象的是( )
A. B. C. D.
【答案】ABD
【解析】根据函数的定义可知,定义域内的每一个只有一个和它对应,
因此不能出现一对多的情况,所以C不是函数图象,ABD是函数图象.故选:ABD.
8.(2023秋·四川眉山·高一校考阶段练习)(多选)下列各组函数中,是同一个函数的有( )
A.与 B.与
C.与 D.与
【答案】AC
【解析】对于A项,的定义域为R,的定义域为R,且,
所以,与为同一个函数,故A项正确;
对于B项,的定义域为R,的定义域为,定义域不一致,
所以,与不为同一个函数,故B项错误;
对于C项,的定义域为,的定义域为,
且解析式表达形式一致,所以,与为同一个函数,故C项正确;
对于D项,解,可得或,
所以定义域为.解可得,,
所以,定义域为.
所以,与的定义域不一致,故D项错误.故选:AC.
9.(2023秋·广东惠州·高一校考阶段练习)若函数的定义域为,则函数的定义域为 .
【答案】
【解析】因为的定义域为,即,所以,
即函数的定义域为,
所以的定义域为不等式组的解集,
解此不等式组得:,
所以函数的定义域为.
10.(2023秋·重庆沙坪坝·高一校考阶段练习)若函数,则 .
【答案】
【解析】由,
.
11.(2023春·甘肃兰州·高一校考开学考试)已知函数,若,则实数a的取值范围为 .
【答案】
【解析】当时,显然不成立;
当时,不等式可化为,解得;
当时,不等式可化为,解得.
综上所述,a的取值范围为或
故答案为:
12.(2023秋·江苏镇江·高一校考阶段练习)已知函数.
(1)求函数的定义域并求;
(2)已知,求的值.
【答案】(1)定义域为或,,;;(2).
【解析】(1)由解析式知:,可得且,故定义域为或,
,
.
(2)由,
所以,显然在定义域内,所以.
13.(2023·全国·高一专题练习)(1)已知是一次函数,且满足,求的解析式;
(2)已知,求的解析式;
【答案】(1);(2)
【解析】(1)由题意,设函数为,
,
,即,
由恒等式性质,得,,,
所求函数解析式为
(2)令,则,,
因为,所以,
所以.
14.(2023秋·江苏无锡·高一校考阶段练习)求下列函数的解析式
(1)设函数是一次函数,且满足,求的解析式
(2)设满足,求的解析式
【答案】(1)或;(2)
【解析】(1)设一次函数的解析式为,
则,
所以,解得,或,
所以或.
(2)由①,
得②,
①②得,即.
15.(2023秋·重庆南岸·高一校考阶段练习)(1)已知函数的定义域为R,求实数的取值范围;
(2)的值域为,求实数的取值范围.
【答案】(1)(2)
【解析】(1)由题意可知:在上恒成立,
当,即时,,即,不合题意;
当,即时,,解得,
综上所述:的取值范围是;
(2)由题意可知:的值域包含,
当时,,因为,可得,
所以的值域为,符合题意;
当时,则,解得,
综上所述:实数的取值范围是.
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题07+向量的应用(8大考点,知识串讲+热考题型+专题训练)-讲义: 这是一份【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题07+向量的应用(8大考点,知识串讲+热考题型+专题训练)-讲义,文件包含寒假作业苏教版2019高中数学高一寒假提升训练专题07向量的应用8大考点知识串讲+热考题型+专题训练原卷版docx、寒假作业苏教版2019高中数学高一寒假提升训练专题07向量的应用8大考点知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题06+向量坐标表示与应用(10大考点,知识串讲+热考题型+专题训练)-讲义: 这是一份【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题06+向量坐标表示与应用(10大考点,知识串讲+热考题型+专题训练)-讲义,文件包含寒假作业苏教版2019高中数学高一寒假提升训练专题06向量坐标表示与应用10大考点知识串讲+热考题型+专题训练原卷版docx、寒假作业苏教版2019高中数学高一寒假提升训练专题06向量坐标表示与应用10大考点知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题04++向量的数量积(8大考点,知识串讲+热考题型+专题训练)-讲义: 这是一份【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题04++向量的数量积(8大考点,知识串讲+热考题型+专题训练)-讲义,文件包含寒假作业苏教版2019高中数学高一寒假提升训练专题04向量的数量积8大考点知识串讲+热考题型+专题训练原卷版docx、寒假作业苏教版2019高中数学高一寒假提升训练专题04向量的数量积8大考点知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源,其中试卷共35页, 欢迎下载使用。