2023-2024学年吉林省白城市通榆县七年级（上）期末数学试卷（含解析）

这是一份2023-2024学年吉林省白城市通榆县七年级（上）期末数学试卷（含解析），共13页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

1.冰箱冷藏室的温度零上6℃，记作+6℃，冷冻室的温度零下18℃，记作( )
A. 18℃B. 12℃C. −18℃D. −24℃
2.−2的绝对值等于( )
A. −12B. 12C. −2D. 2
3.单项式2a2b的系数和次数分别是( )
A. 2，2B. 2，3C. 3，2D. 4，2
4.计算2a2b−3a2b的正确结果是( )
A. ab2B. −ab2C. a2bD. −a2b
5.已知x=2是方程3x−5=2x+m的解，则m的值是( )
A. 1B. −1C. 3D. −3
6.已知一个角的补角等于这个角的3倍，则这个角的度数是( )
A. 45°B. 60°C. 90°D. 120°
7.如图，将一副三角尺按不同的位置摆放，∠α与∠β一定相等的图形个数共有个．( )
A. 4B. 3C. 2D. 1
8.如图，建筑工人砌墙时，经常在两个墙脚的位置分别插一根木桩，然后拉一条直的参照线，这种做法用几何知识解释应是( )
A. 两点之间，线段最短
B. 过一点有且只有一条直线和已知直线平行
C. 垂线段最短
D. 两点确定一条直线
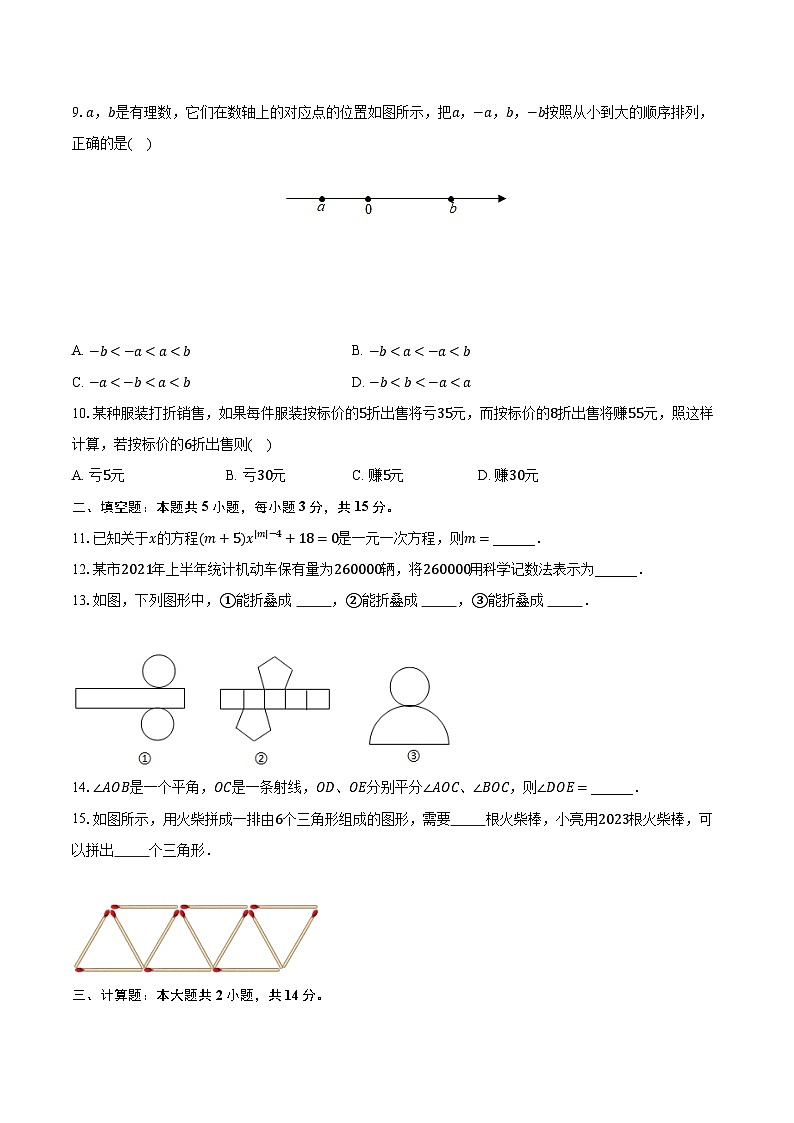
9.a，b是有理数，它们在数轴上的对应点的位置如图所示，把a，−a，b，−b按照从小到大的顺序排列，正确的是( )
A. −b<−aC. −a<−b10.某种服装打折销售，如果每件服装按标价的5折出售将亏35元，而按标价的8折出售将赚55元，照这样计算，若按标价的6折出售则( )
A. 亏5元B. 亏30元C. 赚5元D. 赚30元
二、填空题：本题共5小题，每小题3分，共15分。
11.已知关于x的方程(m+5)x|m|−4+18=0是一元一次方程，则m=______．
12.某市2021年上半年统计机动车保有量为260000辆，将260000用科学记数法表示为______．
13.如图，下列图形中，①能折叠成 ，②能折叠成 ，③能折叠成 ．
14.∠AOB是一个平角，OC是一条射线，OD、OE分别平分∠AOC、∠BOC，则∠DOE=______．
15.如图所示，用火柴拼成一排由6个三角形组成的图形，需要 根火柴棒，小亮用2023根火柴棒，可以拼出 个三角形．
三、计算题：本大题共2小题，共14分。
16.解方程：x−x−13=7−x+35．
17.先化简，再求值：5x2+4−(3x2+5x)−(2x2−6x+5).其中x=−3．
四、解答题：本题共6小题，共61分。解答应写出文字说明，证明过程或演算步骤。
18.(本小题8分)
计算：
(1)(−0.25)×(−25)×(−4)；
(2)(−2)3+4÷(−2)．
19.(本小题8分)
已知a，b互为相反数，c，d互为倒数，m的绝对值是3，试求m2−(a+b+cd)m+(a+b)2023+(−cd)2022的值．
20.(本小题10分)
某人原计划用26天生产一批零件，工作两天后因改变了操作方法，每天比原来多生产5个零件结果提前4天完成任务，问原来每天生产多少个零件？这批零件有多少个？
21.(本小题10分)
某同学做一道数学题，已知两个多项式A、B，B=3x2y−2xy+x+2，试求A+B.这位同学把A+B误看成A−B，结果求出的答案为6x2y+4xy−2x−1．
(1)请你替这位同学求出A+B的正确答案；
(2)当x取任意数值，A−3B的值是一个定值时，求y的值．
22.(本小题12分)
如图，直线AB、CD相交于点O，∠BOD=40°，按下列要求画图并解答问题：
(1)利用三角尺，在直线AB上方画射线OE，使∠BOE=90°；
(2)利用量角器，画∠AOD的平分线OF；
(3)在你所画的图形中，求∠AOD与∠EOF的度数．
23.(本小题13分)
如图，点A从原点出发沿数轴向左运动，同时，点B也从原点出发沿数轴向右运动，4秒后，两点相距16个单位长度，已知点B的速度是点A的速度的3倍(速度单位：单位长度/秒)．
(1)求出点A、点B运动的速度，并在数轴上标出A、B两点从原点出发运动4秒时的位置；
(2)若A、B两点从(1)中的位置开始，仍以原来的速度同时沿数轴向左运动，再过几秒时，原点恰好处在AB的中点？
(3)若A、B两点从(1)中的位置开始，仍以原来的速度同时沿数轴向左运动时，另一点C同时从原点O位置出发向B点运动，且C的速度是点A的速度的一半；当点C运动几秒时，C为AB的中点？
答案和解析
1.【答案】C
【解析】【分析】
本题考查了正数和负数，相反意义的量用正数和负数表示，确定相反意义的量是解题关键．用正数表示零上，则负数表示零下．
【解答】
解：温度零上6℃，记作+6℃，冷冻室的温度零下18℃，记作−18℃，
故选：C．
2.【答案】D
【解析】【分析】
本题考查了绝对值的性质：一个正数的绝对值是它本身，一个负数的绝对值是它的相反数，0的绝对值是0．
根据绝对值的性质：一个负数的绝对值是它的相反数解答即可．
【解答】
解：根据绝对值的性质，
|−2|=2．
故选：D．
3.【答案】B
【解析】【分析】
本题考查了单项式，理解单项式的系数和次数是解题的关键．
根据单项式的次数是所有字母指数的和，单项式的系数是数字因数，可得答案．
【解答】
解：2a2b的系数为2，次数是3．
故选：B．
4.【答案】D
【解析】【分析】
本题主要考查合并同类项，熟练掌握合并同类项的法则是解题的关键．根据合并同类项的法则：把同类项的系数相加，所得结果作为系数，字母和字母的指数不变即可得．
【解答】
解：原式=(2−3)a2b=−a2b，
故选：D．
5.【答案】D
【解析】【分析】
本题主要考查一元一次方程的解的定义，掌握方程的解满足方程是解题的关键．把x=2代入方程3x−5=2x+m可得到关于m的方程，解方程可求得m的值．
【解答】
解：因为x=2是方程3x−5=2x+m的解，
所以把x=2代入方程可得6−5=4+m，
解得m=−3，
故选：D．
6.【答案】A
【解析】解：设这个角为x°，由题意得：
180−x=3x，
解得：x=45．
故选：A．
首先这个角为x°，则它的补角为(180−x)°，根据题目所给等量关系列出方程，再解方程即可．
此题主要考查了余角和补角，关键是掌握余角：如果两个角的和等于90°(直角)，就说这两个角互为余角．即其中一个角是另一个角的余角．
补角：如果两个角的和等于180°(平角)，就说这两个角互为补角．即其中一个角是另一个角的补角．
7.【答案】C
【解析】【分析】：
本题考查了余角和补角，是基础题，熟记概念与性质是解题的关键．根据平角的定义，同角的余角相等，等角的补角相等和邻补角的定义对各小题分析判断即可得解．
【解答】
解：第1个图，∠α+∠β=180°−90°，互余；
第2个图，根据同角的余角相等，∠α=∠β；
第3个图，∠α+∠β=180°，互补．
第4个图，根据等角的补角相等∠α=∠β=135°；
综上所述，∠α与∠β一定相等的图形个数共有2个，
故选：C．
8.【答案】D
【解析】【分析】
此题主要考查了直线的性质，正确把握直线的性质联系实际生活是解题关键．
直接利用直线的性质分析得出答案．
【解答】
解：建筑工人砌墙时，经常在两个墙脚的位置分别插一根木桩，然后拉一条直的参照线，
这种做法用几何知识解释应是：两点确定一条直线．
故选：D．
9.【答案】B
【解析】【分析】
此题主要考查了有理数的大小比较的方法，以及数轴的特征．根据图示，可得：a<0【解答】
解：因为a<0所以0<−a所以−b故选：B．
10.【答案】A
【解析】【分析】：
此题主要考查了一元一次方程的应用，正确找出等量关系是解题关键．设每件服装标价为x元，再根据无论亏本或盈利，其成本价相同，列出方程，求出x的解，最后根据成本价=服装标价×折扣即可得出答案．
【解答】
解：设每件服装标价为x元，根据题意得：
0.5x+35=0.8x−55，
解得：x=300．
则每件服装标价为300元，
成本价是：300×50%+35=185(元)，
故按标价的6折出售则：300×0.6−185=−5，即亏5元．
故选：A．
11.【答案】5
【解析】解：∵关于x的方程(m+5)x|m|−4+18=0是一元一次方程，
∴m+5≠0且|m|−4=1，
解得m=5．
故答案为：5．
根据题意得出m+5≠0且|m|−4=1，据此可得m的值．
本题考查了一元一次方程的定义，列出关于m的方程是解此题的关键．
12.【答案】2.6×105
【解析】解：260000=2.6×105，
故答案为：2.6×105．
科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数；当原数的绝对值<1时，n是负整数．据此解答即可．
此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数，表示时关键要确定a的值以及n的值．
13.【答案】圆柱，
五棱柱
圆锥

【解析】【分析】
本题考查了展开图折叠成几何体，能够正确利用展开图的形状是解题的关键．根据圆柱、五棱柱、圆锥的展开图形状特点判断即可．
【解答】
解：①能折叠成圆柱，②能折叠成五棱柱，③能折叠成圆锥．
故答案为：圆柱，五棱柱，圆锥．
14.【答案】90°
【解析】解：∵OD、OE分别平分∠AOC、∠BOC，
∴∠DOC=12∠AOC，∠EOC=12∠BOC，
∴∠DOC+∠EOC=12(∠AOC+∠BOC)，
∴∠DOE=12∠AOB=12×180°=90°．
故答案为90°．
根据角平分线定义得到∠DOC=12∠AOC，∠EOC=12∠BOC，把它们相加得到∠DOE=12∠AOB，然后根据平角的定义进行计算．
本题考查了角平分线的定义：从一个角的顶点出发，把这个角分成相等的两个角的射线叫做这个角的平分线．
15.【答案】13；1011．
【解析】【分析】
观察图形的变化先求出前几个图形需要的火柴棒根数，即可发现规律：由n个三角形组成的图形，需要(2n+1)根火柴棒，进而可求几个．
本题考查了规律型：图形的变化类，解决本题的关键是根据图形的变化寻找规律．
【解答】
解：观察图形的变化可知：
由1个三角形组成的图形，需要2×1+1=3根火柴棒；
由2个三角形组成的图形，需要2×2+1=5根火柴棒；
由3个三角形组成的图形，需要2×3+1=7根火柴棒；
…，
发现规律：
由n个三角形组成的图形，需要(2n+1)根火柴棒；
所以由6个三角形组成的图形，需要2×6+1=13根火柴棒；
因为2n+1=2023，
所以n=1011，
所以用2023根火柴棒，可以拼出1011个三角形．
故答案为：13；1011．
16.【答案】解：x−x−13=7−x+35．
去分母，得15x−5(x−1)=105−3(x+3)
去括号，得15x−5x+5=105−3x−9
移项，得15x−5x+3x=105−5−9
合并同类项，得13x=91
化系数为1，得x=7．
【解析】本题是一道一元一次方程的计算题，考查了学生解一元一次方程的步骤．
根据解一元一次方程的步骤：去分母，去括号，移项，合并同类项，化系数为1这些步骤进行就可以了．
17.【答案】解：5x2+4−(3x2+5x)−(2x2−6x+5)
=5x2+4−3x2−5x−2x2+6x−5
=(5−3−2)x2+(−5+6)x+4−5
=x−1
当x=−3时，
原式=−3−1
=−4．
【解析】本题主要考查整式的加减−化简求值，解题的关键是熟练掌握去括号、合并同类项法则．
原式去括号、合并同类项化简后，再把x的值代入计算可得．
18.【答案】解：(1)(−0.25)×(−25)×(−4)
=(−0.25)×[(−25)×(−4)]
=(−0.25)×100
=−25．
(2)(−2)3+4÷(−2)
=−8+(−2)
=−10．
【解析】(1)根据乘法结合律，求出算式的值即可；
(2)首先计算乘方，然后计算除法，最后计算加法，求出算式的值即可．
此题主要考查了有理数的混合运算，要熟练掌握，注意明确有理数混合运算顺序：先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算，另外，注意乘法运算定律的应用．
19.【答案】解：依题意得a+b=0，
cd=1，
m=3或−3．
当m=3时，
m2−(a+b+cd)m+(a+b)2023+(−cd)2022
=9−(0+1)×3+0+1
=7；
当m=−3时，
m2−(a+b+cd)m+(a+b)2023+(−cd)2022
=9−(0+1)×(−3)+0+1
=13．
【解析】根据相反数、倒数和绝对值的特征，得到a+b=0、cd=1、m=±3，再将数值代入求出结果．
本题考查了有理数的混合运算，关键根据绝对值的运算分两种情况解答．
20.【答案】解：设原来每天生产x个零件，根据题意可得：
26x=2x+(26−2−4)(x+5)，
解得：x=25，
故26×25=650(个)．
答：原来每天生产25个零件，这批零件有650个．
【解析】此题主要考查了一元一次方程的应用，根据题意表示出零件的总个数是解题关键．
设原来每天生产x个零件，表示出所有零件的个数，进而得出等式求出即可．
21.【答案】解(1)∵B=3x2y−2xy+x+2，A−B=6x2y+4xy−2x−1，
∴A+B=(A−B)+2B
=6x2y+4xy−2x−1+2(3x2y−2xy+x+2)
=6x2y+4xy−2x−1+6x2y−4xy+2x+4
=12x2y+3；
(2)A−3B=A+B−4B
=12x2y+3−4(3x2y−2xy+x+2)
=12x2y+3−12x2y+8xy−4x−8
=8xy−4x−5
=(8y−4)x−5，
∵当x取任意数值，A−3B的值是一个定值，
∴8y−4=0，
∴y=12．
【解析】(1)根据A+B=(A−B)+2B列出代数式，去括号合并同类项即可；
(2)先根据A−3B=A+B−4B列出代数式，去括号合并同类项求出结果，再根据当x的取任意数值，A−3B的值是一个定值得出8y−4=0，即可求解．
本题考查的是整式的加减，熟知整式加减的实质是去括号、合并同类项是解答此题的关键．
22.【答案】解：(1)如图，射线OE即为所求作．
(2)如上图，射线OF即为所求作．
(3)因为∠AOB是平角，∠BOD=40°，
所以∠AOD=180°−∠BOD=140°，
所以OF平分∠AOD，
所以∠AOF=12∠AOD=70°，
因为∠AOE=90°，
所以∠EOF=∠AOE−∠AOF=90°−70°=20°．
【解析】本题考查作图，角平分线的定义等知识，解题的关键是理解题意，灵活运用所学知识解决问题．
(1)，(2)根据要求画出图形即可．
(3)利用平角的定义求出∠AOD，∠AOF即可解决问题．
23.【答案】解：(1)设点A的速度为每秒t个单位长度，则点B的速度为每秒3t个单位长度．
依题意有：4t+4×3t=16，
解得：t=1，
故点A的速度为每秒1个单位长度，点B的速度为每秒3个单位长度，
则A到达的位置为：−4，B到达的位置是12，在数轴上的位置如图：
，
答：点A的速度为每秒1个单位长度，点B的速度为每秒3个单位长度；，
(2)设y秒时，原点恰好处在两个动点的正中间，根据题意得：
4+y=12−3y
解得：y=2，
答：再过2秒时，原点恰好处在AB的中点；
(3)设当C运动z秒后，C为AB的中点，
由题意可得：4+z+12z=12(16−3z+z)，
解得：z=85，
答：当点C运动85秒时，C为AB的中点．
【解析】此题主要考查了一元一次方程的应用，关键是正确理解题意，找出题目中的等量关系，设出未知数，列出方程．
(1)设动点A的速度是t单位长度/秒，那么动点B的速度是3t单位长度/秒，然后根据4秒后，两点相距16个单位长度即可列出方程解决问题；
(2)设y秒时，原点恰好处在两个动点的正中间，那么A运动的长度为y，B运动的长度为3y，然后根据(1)的结果和已知条件即可列出方程解题；
(3)设当C运动z秒后，C为AB的中点，由中点定义得出方程，即可解答．