

数学九年级下册7.5 解直角三角形第1课时教学设计
展开课题
7.5 解直角三角形(第1课时)
主备人
执教者
课型
新授课
课 时
1
授课时间
教
学
目
标
1.使学生了解解直角三角形的概念,能运用直角三角形的角与角、边与边、边与角关系解直角三角形;
2.通过学生的探索讨论发现解直角三角形所需的条件,使学生了解体会用化归的思想方法将未知问题转化为已知问题去解决;
3.通过问题情境,以及对解直角三角形所需的条件的探究,运用数学知识解决一些简单的实际问题,渗透“数学建模”的思想.
教学
重难点
直角三角形的解法;三角函数在解直角三角形中的灵活运用.
教学法指导
小组合作讨论、讲练结合法
教具准备
多媒体课件
集 体 智 慧
个性设计
教学后记
新课引入——情景导入
五星红旗你是我的骄傲,五星红旗我为你自豪……
如何测量旗杆的高度?请同学们说说你的想法.
实践探索
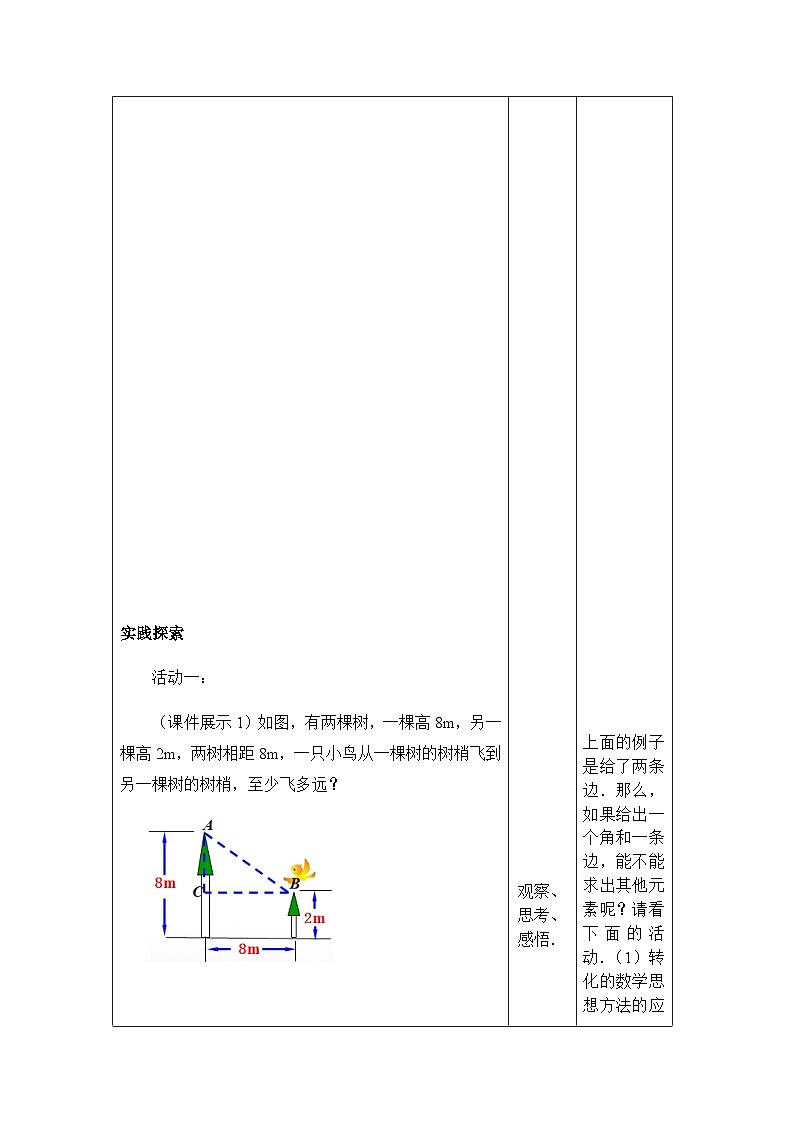
活动一:
(课件展示1)如图,有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞多远?
活动二:
A
(课件展示2)如图,为测量旗杆的高度,在C点测得A点的仰角为30°,点C到点B的距离56.3,求旗杆的高度(精确到0.1m).
B
C
解:略.
归纳总结
同学们回答的非常好,通过上面的两个活动,若要完整解该直角三角形,还需求出哪些元素?
如图,在Rt△ABC中, ∠C为直角,其余5个元素之间有以下关系:
(1)三边之间关系:
a2+b2=c2(勾股定理).
(2)锐角之间的关系:
∠A+∠B=90°(直角三角形的两个锐角互余).
(3)边角之间的关系:
学生交流讨论归纳(课件展示讨论的条件)
师总结:解直角三角形,有下面
两种情况(其中至少有一边) :
已知两条边(一直角边一
斜边;两直角边) ;
(2) 已知一条边和一个锐角(一直角边一锐角;一斜边一锐角).
自然就可以得出“定义” .
例题讲解
例1 在Rt△ABC中,∠C=90°,∠A=30°,a=5.解这个直角三角形.
例2 已知:在Rt△ABC中,∠C=90°,a=104,b= 20.49.
(1)求c的值(精确到0.01);
(2)求∠A、∠B的大小(精确到0.01°).
知识巩固
1.在Rt△ABC中,∠C=90°,根据下列条件解直角三角形(边长精确到0.1,角度精确到0.1°):
求:(1)a=9 ,b=6;(2) ∠A=18°,∠C=13.
2.如图,某地修建高速公路,要从B地向C地修一座隧道(B、C在同一水平面上).为了测量B、C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100m到达A处,在A处观察B地的俯角为30°,求:B、C两地之间的距离.
课堂小结
通过今天的学习,你学会了什么?
解直角三角
形的概念
(勾股定理)
三边之间关系
两锐角之间关系
边角之间关系
(锐角三角函数)
简单应用
布置作业
(1)必做题:
(2)选做题:如图所示,施工队准备在一段斜坡上铺上台阶方便通行.现测得斜坡上铅垂的两棵树间水平距离AB=4米,斜面距离BC=4.25米,斜坡总长DE=85米.(1)求坡角∠D的度数(结果精确到1°);
(2)若这段斜坡用厚度为17cm的长方体台阶来铺,需要铺几级台阶?
(参考数据:cs20°≈0.94,sin20°≈0.34,sin18°≈0.31,
cs18°≈0.95)
17cm
A
B
C
D
E
F
积极思考,回答问题——大多数学生会凭直觉发表自己的观点,有的用尺子度量,有的说我们可以构建直角三角形解决.
观察、思考、感悟.
观察、思考,并归纳、小结得出“在直角三角形中,除直角外,只要知道其中2个元素(至少有一个是边)”.
1.根据解直角三角形定义和方法进行分析.
2.思考多种方法,选择最简便的方法.
例2由学生独立分析,板练完成,并作自我评价,以掌握方法.
积极思考解决办法——运用本节课所学数学知识解决问题,关键要对知识灵活运用.
共同小结.
课后完成必做题,并根据自己的能力水平确定是否选做思考题.
通过身边的情境让学生思考、交流、发言,调动学生的课堂参与的积极性,激发了他们研究的兴趣和探究的激情.
上面的例子是给了两条边.那么,如果给出一个角和一条边,能不能求出其他元素呢?请看下面的活动.(1)转化的数学思想方法的应用,把实际问题转化为数学模型解决 ;
(2)巩固解直角三角形的定义和目标,初步体会解直角三角形的方法——直角三角形的边角关系(勾股定理、两锐角互余、锐角三角函数)使学生体会到 “在直角三角形中,除直角外,只要知道其中2个元素(至少有一个是边)就可以求出其余的3个元素” 交流讨论;归纳总结 .
这是这节课的重点,让学生归纳和讨论,能让他们深刻理解解直角三角形有几种情况,必须满足什么条件能解出直角三角形 ,给学生展示的平台,增强学生的兴趣及自信心.
通过例题学会灵活运用直角三角形有关知识解直角三角形,并能熟练分析问题,掌握所学基础知识及基本方法,并进一步提高学生“执果索因”的能力.
使学生巩固利用直角三角形的有关知识解决实际问题,考察建立数学模型的能力,转化的数学思想在学习中的应用,提高学生分析问题、解决问题的能力,以及在学习中还存在哪些问题,及时反馈矫正.
通过反思、归纳,培养概括能力;帮助学生总结经验教训,巩固知识技能,提高认知水平.
学生可根据自己的能力去自主选做.这样就能实现《课程标准》中所要求的“让不同层次的学生得到不同的发展”.
初中数学苏科版九年级下册7.5 解直角三角形第2课时教学设计: 这是一份初中数学苏科版九年级下册7.5 解直角三角形第2课时教学设计,共6页。
数学九年级下册7.2 正弦、余弦第1课时教学设计及反思: 这是一份数学九年级下册7.2 正弦、余弦第1课时教学设计及反思,共3页。
初中7.1 正切第2课时教案设计: 这是一份初中7.1 正切第2课时教案设计,共5页。













