(期末典型真题)图形计算-广东省深圳市2023-2024学年六年级上册数学期末真题精选(北师大版)
展开试卷说明:本试卷试题精选自广东省深圳市近两年六年级上学期期末真题试卷,难易度均衡,适合广东省深圳市及使用北师大版教材的六年级学生期末复习备考使用!
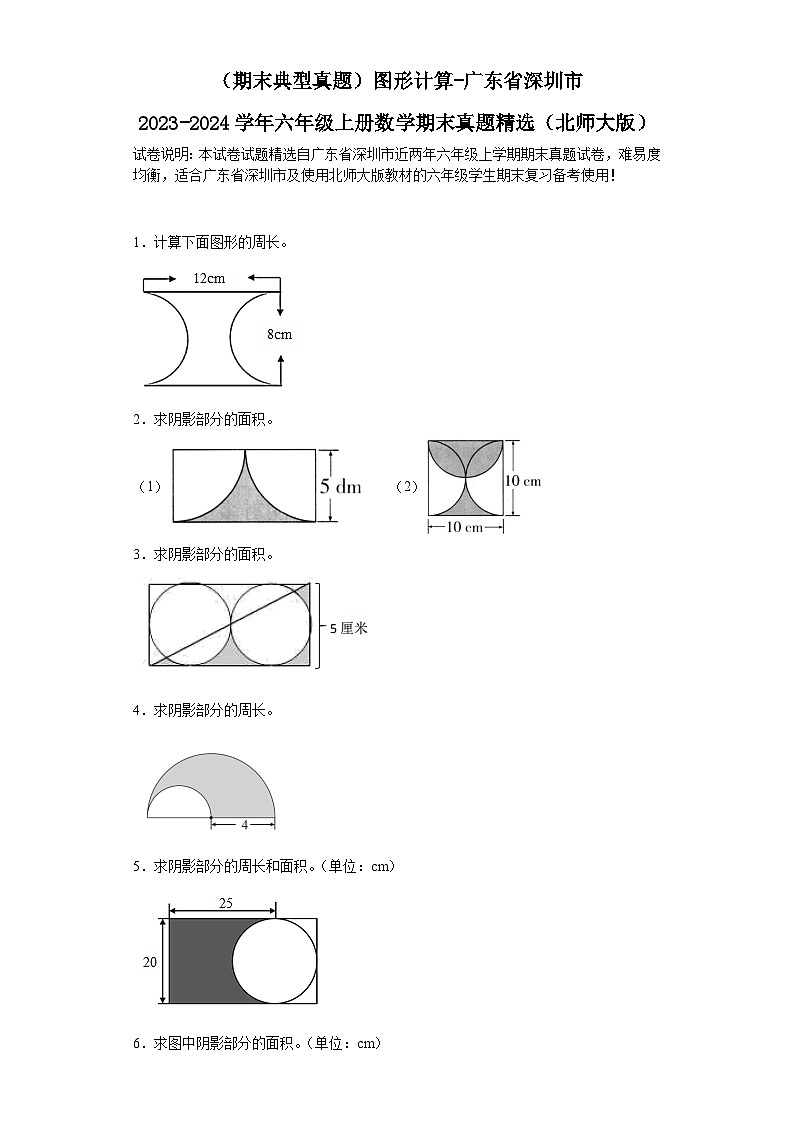
1.计算下面图形的周长。
2.求阴影部分的面积。
(1) (2)
3.求阴影部分的面积。
4.求阴影部分的周长。
5.求阴影部分的周长和面积。(单位:cm)
6.求图中阴影部分的面积。(单位:cm)
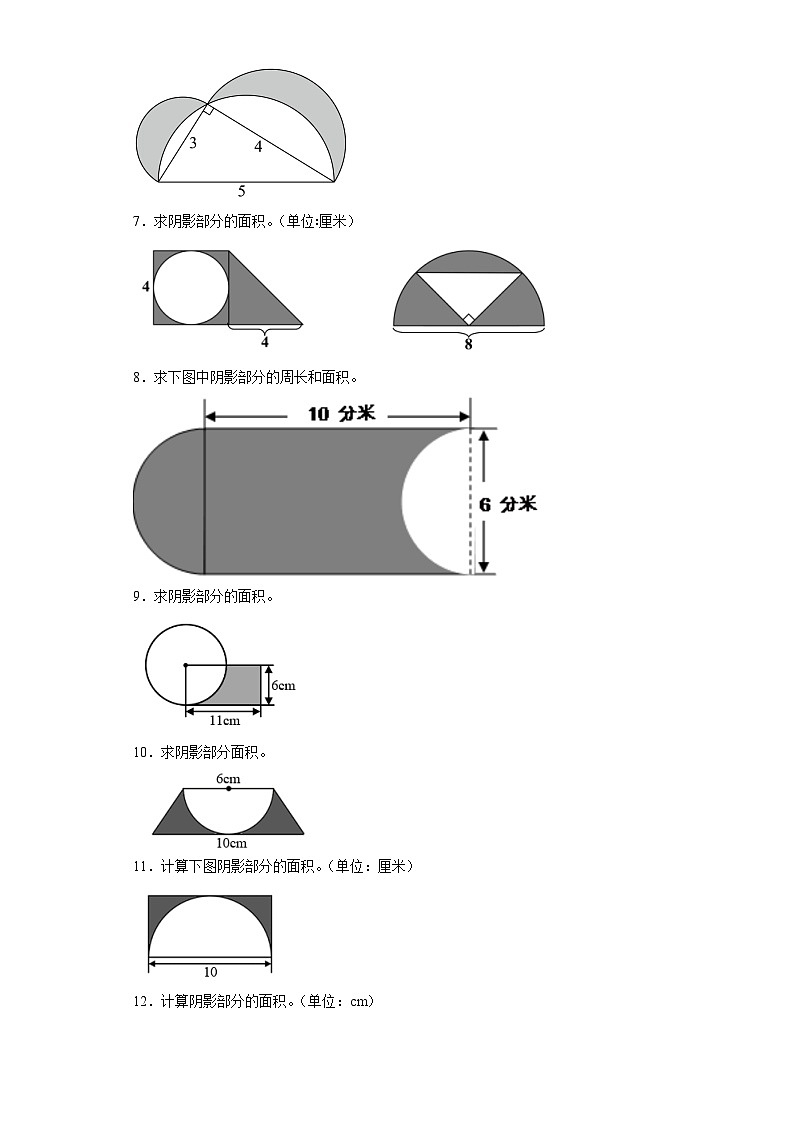
7.求阴影部分的面积。(单位∶厘米)
8.求下图中阴影部分的周长和面积。
9.求阴影部分的面积。
10.求阴影部分面积。
11.计算下图阴影部分的面积。(单位:厘米)
12.计算阴影部分的面积。(单位:cm)
13.求图中阴影部分的面积。
14.计算阴影部分的面积
15.计算阴影部分的周长。
16.计算下图阴影部分面积.
17.求下图阴影部分的面积。(单位:cm)
18.已知圆的周长是18.84dm。求阴影部分的面积。(单位:分米)
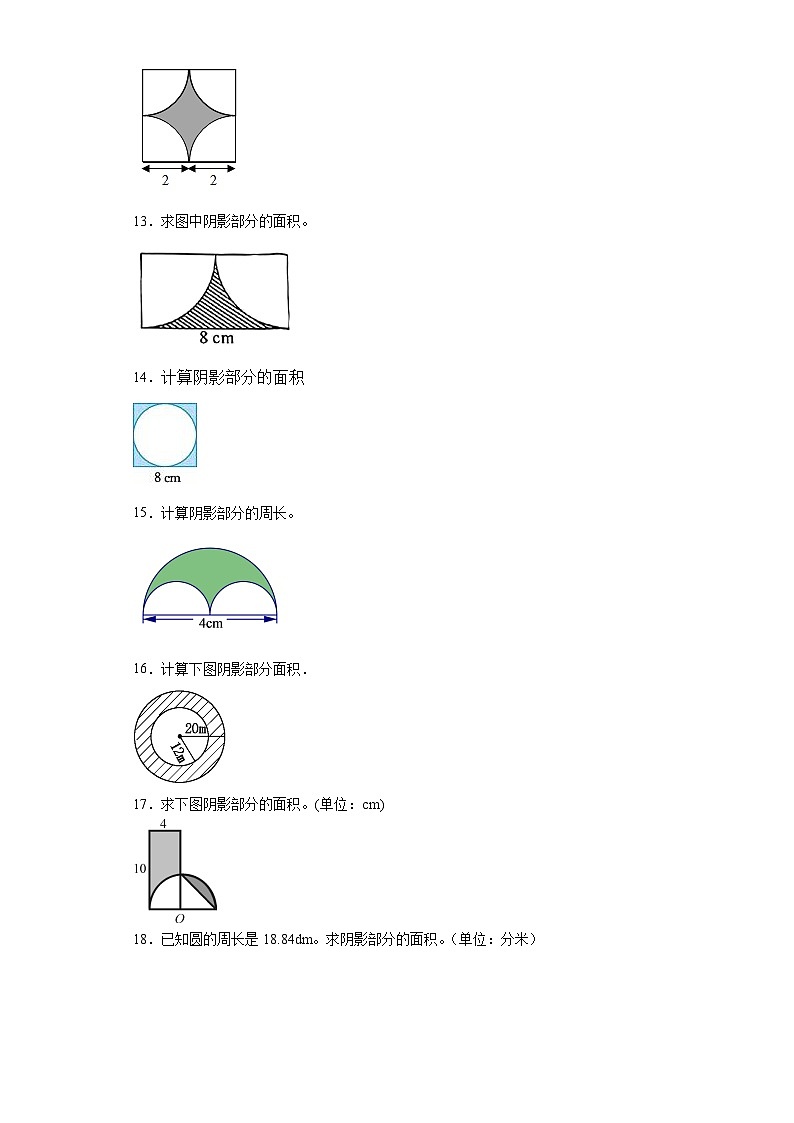
19.用字母表示下列图形中阴影部分的面积.
(1)
(2)
(3)
20.求阴影部分的面积。
21.计算下面图形阴影部分的周长和面积。(单位:cm)
22.计算下面图形阴影部分的周长和面积。
23.求阴影部分的面积
24.计算下图中阴影部分的面积.
25.计算阴影部分的面积和周长。(单位:厘米)
26.求下列图形阴影部分的面积。(单位:厘米)
27.求阴影部分的周长和面积
28.求阴影部分的面积。(单位:cm)。
29.求阴影部分的面积。(单位:厘米)
30.计算阴影部分面积。(取3.14)
31.计算下面图形阴影部分的面积。
32.求阴影部分面积。
33.求下图阴影部分的面积。(单位:米。)
34.学校的操场是下面的形状,请计算出操场的周长和面积。
35.如图所示,图中长方形的面积是45平方厘米,宽是5厘米,求阴影部分的面积.
36.计算下面圆的面积和周长。
圆的周长:
圆的面积:
37.求出下列阴影部分的面积(单位:厘米)。
38.计算下面图形的周长和面积。
39.求阴影部分的面积。(单位:cm)
40.求下图中阴影部分的面积。(单位:cm)
41.算图高手。(求阴影部分的面积)
42.求出第一个图形的周长和第二个图形阴影部分的面积.(单位:dm)
43.求阴影部分的面积。
44.求下面图形中涂色部分的面积。
45.计算下面图形的周长。
46.计算下面图形阴影部分的面积。
47.计算下图的阴影部分的面积。
48.求图中阴影部分面积。
49.计算下图阴影部分的面积和周长。
50.计算下图中阴影部分的面积。
51.求下面各图形中阴影部分的面积。
(1) (2) (3)
52.求出图中阴影部分的周长和面积。(单位:分米)
53.求阴影部分的面积。(单位:厘米)
54.求图中阴影的周长(单位:厘米)。
55.求下图阴影部分的面积.
56.求阴影部分的面积。(单位:厘米)
57.计求下列图形的周长(单位:米)
58.求下图中的阴影面积。(r=10cm)
参考答案:
1.49.12厘米
【分析】通过观察图形可知,它的周长等于直径是8厘米的圆的周长加上12厘米的2倍,根据圆的周长公式:,把数据代入公式解答。
【详解】3.14×8+12×2
=25.12+24
=49.12(厘米)
它的周长是49.12厘米。
2.(1)10.75dm²;
(2)50cm²
【详解】(1)5×2×5-3.14×5²÷2=10.75(dm²)
(2)10×10÷2=50(cm²)
3.5.375平方厘米
【分析】通过观察可知,长方形的长是两个圆的直径长度,也是三角形的长直角边,长方形的宽是一个圆的直径长度,也是三角形的短直角边,阴影部分的面积=三角形面积-一个圆面积,三角形面积=底×高÷2,圆面积=,以此解答即可。
【详解】5×2×5÷2-3.14×(5÷2)2
=25-19.625
=5.375(平方厘米)
【点睛】解答此题的关键是理解阴影部分左下边的小半圆与空白部分右上边的小半圆面积相等。
4.22.84
【分析】观察该图形,阴影部分的周长等于半径是4的圆的周长的一半+直径是4的圆的周长的一半+4,利用圆的周长公式:C=πd=2πr,代入数值即可解答。
【详解】3.14×4×2÷2+3.14×4÷2+4
=12.56+6.28+4
=22.84
5.101.4cm;343
【分析】阴影部分的周长等于圆的周长一半加上1个20再加上2个25的和;
阴影部分的面积等于长为25cm、宽为20cm的长方形面积减去圆的面积的一半。
【详解】周长:3.14×20÷2+20+25×2
=62.8÷2+20+50
=31.4+20+50
=101.4(cm)
面积:25×20-3.14×÷2
=500-3.14×100÷2
=500-314÷2
=500-157
=343()
6.6cm2
【分析】阴影部分的面积=直径3cm的半圆面积+直径4cm的半圆面积+直角三角形的面积-直径5cm的半圆面积,半圆的面积=圆周率×半径的平方÷2,三角形面积=底×高÷2,据此列式计算。
【详解】3.14×(3÷2)2÷2+3.14×(4÷2)2÷2+3×4÷2-3.14×(5÷2)2÷2
=3.14×1.52÷2+3.14×22÷2+6-3.14×2.52÷2
=3.14×2.25÷2+3.14×4÷2+6-3.14×6.25÷2
=3.5325+6.28+6-9.8125
=6(cm2)
图中阴影部分的面积是6cm2。
7.11.44平方厘米;17.12平方厘米。
【分析】第一个通过图形可以看出,是一个正方形和一个圆组成在一起,阴影部分=正方形面积-圆的面积+三角形面积。
第二个图看出,是一个半圆,内部一个直角三角形,三角形的边长是圆的半径。阴影部分面积=半圆面积-三角形面积。
正方形面积=边长×边长;三角形面积=底×高÷2;圆的面积=π×半径×半径
【详解】(1)正方形面积:4×4=16(平方厘米),
三角形面积:4×4÷2
=16÷2
=8(平方厘米)
圆的半径:4÷2=2(厘米),
圆的面积:3.14×2×2
=6.28×2
=12.56(平方厘米)
阴影面积:16+8-12.56
=24-12.56
=11.44(平方厘米);
(2)圆的半径:8÷2=4(厘米)
半圆面积:3.14×4×4÷2
=50.24÷2
=25.12(平方厘米)
三角形面积:4×4÷2
=16÷2
=8(平方厘米)
阴影面积:25.12-8=17.12(平方厘米)
【点睛】解题的关键在于把整个图形的面积算出来,减去空白的面积即可求出阴影的。
8.周长:38.84分米;面积:60平方分米
【详解】周长:3.14×6+2×10
=18.84+20
=38.84(分米)
面积:10×6=60(平方分米)
9.37.74cm2
【分析】观察图形可知,阴影部分面积=长11cm,宽是6cm的长方形面积-半径是6cm圆的面积的,根据长方形面积公式:面积=长×宽,圆的面积公式:面积=π×半径2,代入数据,即可解答。
【详解】11×6-3.14×62×
=66-3.14×36×
=66-113.04×
=66-28.26
=37.74(cm2)
10.9.87cm2
【分析】阴影部分的面积等于一个上底为6厘米,下底为10厘米,高为(6÷2)厘米的梯形的面积减去个半径为(6÷2)厘米的圆的面积,分别利用梯形和圆的面积公式,求出这两个图形的面积,再相减即可求出阴影部分的面积。
【详解】(6+10)×(6÷2)÷2-×3.14×(6÷2)2
=16×3÷2-×3.14×32
=24-×3.14×9
=24-14.13
=9.87(cm2)
即阴影部分的面积是9.87cm2。
11.10.75平方厘米
【分析】观察图形可知,用长方形的面积减去半圆的面积即可求出阴影部分的面积。长方形的面积=长×宽,半圆的面积=πr2÷2,据此解答。
【详解】10÷2=5(厘米)
10×5-3.14×52÷2
=50-78.5÷2
=50-39.25
=10.75(平方厘米)
阴影部分的面积是10.75平方厘米。
12.3.44cm2
【分析】由图可知:阴影部分的面积=边长是2+2=4厘米的正方形面积-半径是2厘米的圆的面积,代入数据计算即可。
【详解】(2+2)×(2+2)-3.14×22
=16-12.56
=3.44(cm2)
13.6.88cm2
【分析】阴影部分的面积等于长方形面积减去半径是(8÷2)厘米半径的圆的面积。
【详解】圆的半径=长方形的宽=8÷2=4(cm)
8×4-3.14×42×
=32-3.14×16×
=32-3.14×8
=32-25.12
=6.88(cm2)
阴影部分的面积是6.88cm2。
14.13.76cm2.
【分析】观察图形可知,阴影部分的面积=正方形的面积-空白圆的面积,正方形的面积=边长×边长,圆的面积:S=πr2 , 据此列式解答.
【详解】解:8÷2=4(cm)8×8-3.14×42
=8×8-3.14×16
=64-50.24
=13.76(cm2)
答:阴影部分的面积是13.76cm2.
15.12.56cm
【分析】由图可知:阴影部分的周长=直径是4厘米的圆的周长的一半+直径是(4÷2)厘米的圆的周长,据此解答。
【详解】3.14×4÷2+3.14×(4÷2)
=3.14×2+3.14×2
=3.14×4
=12.56(cm)
16.803.84 m2
【详解】略
17.32cm2
【详解】4×10+4×4×3.14÷4−4×4×3.14÷4−4−4×4÷2
=40−8
=32(cm2)
18.13.5dm2
【分析】根据圆的周长公式C=2πr求出圆的半径,即梯形的上底与高的长度,然后根据梯形的面积公式S=(a+b)h÷2解答即可。
【详解】18.84÷3.14÷2
=6÷2
=3(dm)
(3+6)×3÷2
=9×3÷2
=27÷2
=13.5(dm2)
19.(1)2a-π
(2)mn-nx
(3)x2-4y2
【解析】略
20.56.52平方米
【分析】把左下角的阴影半圆移补到空白半圆处,则阴影部分形成一个大半圆。根据圆的面积=π求出整圆的面积,再除以2即可求出半圆的面积。
【详解】3.14×62÷2
=113.04÷2
=56.52(平方米)
【点睛】本题考查阴影部分面积,通过移补法把不规则图形转化为规则图形。
21.周长:49.12cm
面积:45.76cm2
【分析】观察图形可知,阴影部分的周长,就是直径是8cm的圆的周长+长方形的两条长;阴影部分面积等于长是12cm,宽是8cm长方形面积-直径是8cm圆的面积;根据圆的周长公式:周长=π×直径;圆的面积公式:π×半径2,代入数据,即可解答。
【详解】周长:3.14×8+12×2
=25.12+24
=49.12(cm)
面积:12×8-3.14×(8÷2)2
=96-3.14×42
=96-3.14×16
=96-50.24
=45.76(cm2)
22.周长是36.56cm,面积是37.76cm2
【分析】根据图可知,阴影部分的周长相当于的圆弧加上一条边是10cm,一条边是14cm的长度,根据圆的周长公式:C=2πr,把数代入公式即可求解;
阴影部分的面积相当于上底是8cm,下底是14cm,高是8cm的梯形,减去一个圆的面积,根据梯形的面积公式:(上底+下底)×高÷2;圆的面积公式:S=πr2,把数代入公式即可求解。
【详解】2×8×3.14×+10+14
=50.24×+24
=12.56+24
=36.56(cm)
(8+14)×8÷2-3.14×8×8×
=22×8÷2-50.24
=88-50.24
=37.76(cm2)
所以阴影部分的周长是36.56cm,面积是37.76cm2。
23.11.44平方厘米
【详解】(4+8)×4÷2=24(平方厘米) 42×3.14÷4=12.56(平方厘米) 24 - 12.56=11.44(平方厘米)
24.21.87cm2
【详解】6×6-3.14×(6÷2)2÷2=21.87(cm2)
25.47.1平方厘米;50.24厘米
【分析】阴影部分的面积=大半圆的面积-两个较小半圆的面积之和;
阴影部分的周长=三个半圆的周长之和。
【详解】(10+6)÷2=8(厘米),6÷2=3(厘米),10÷2=5(厘米)
阴影部分面积:3.14×82÷2-3.14×52÷2-3.14×32÷2
=100.48-39.25-14.13
=47.1(平方厘米)
阴影部分的周长:3.14×(10+6)÷2+3.14×6÷2+3.14×10÷2
=25.12+9.42+15.7
=50.24(厘米)
26.84.78平方厘米;86平方厘米
【分析】根据圆环的面积公式:S=π(R2-r2),代入数据解答。
阴影部分的面积=正方形的面积-空白圆的面积;圆的直径相当于正方形的边长,根据正方形的面积=边长×边长,圆的面积公式:S=πr2,代入数据即可求出两部分的面积,再相减即可。
【详解】3.14×(62-32)
=3.14×(36-9)
=3.14×27
=84.78(平方厘米)
第一个阴影部分是84.78平方厘米。
20÷2=10(厘米)
20×20-3.14×102
=20×20-3.14×100
=400-314
=86(平方厘米)
第二个阴影部分是86平方厘米。
27.C=35.42(cm) S=45.87(cm²);
【解析】略
28.3.72cm
【分析】通过观察可知,阴影部分面积=梯形面积-半圆面积,梯形面积=(上底+下底)×高÷2,半圆面积=,代数解答即可。
【详解】(2×2+6)×2÷2-
=10-6.28
=3.72(cm)
29.11.44厘米,13.76厘米
【详解】×(4+8)×4-×π×42=11.44(平方厘米)
82-π×()2=13.76(平方厘米)
30.12.56平方厘米
【分析】根据三角形内角和180度以及扇形的特点,两个圆的半径相等,图中两个扇形加起来正好是一个圆心角是90度的扇形,即一个圆的。据此计算。
【详解】3.14×42×
=3.14×16×
=12.56(平方厘米)
31.32.25cm2
【分析】由图可知,阴影部分的面积=圆的面积-中间空白的面积+两个拐角部分的面积,圆的面积公式:S=πr2,中间空白部分面积=半径为10cm的半圆的面积-正方形的面积,两个拐角的面积=(正方形的面积-圆的面积)÷2,正方形的面积=边长×边长,据此解答即可。
【详解】
=
=
=
=
=21.5+10.75
=32.25(cm2)
32.11.44cm2
【分析】根据图可知,阴影部分面积=直角三角形的面积-圆的面积,根据三角形的面积公式:底×高÷2;圆的面积公式:S=πr2,把数代入公式即可求解。
【详解】6×8÷2-2×2×3.14
=24-12.56
=11.44(cm2)
所以阴影部分的面积是11.44cm2。
33.6平方米
【分析】观察图形可知,阴影部分面积=直径是3米的圆的面积一半+直径是4米的圆的面积一半+底是3米,高是4米的三角形面积-直径是5米的圆的面积一半,根据圆的面积公式:面积=π×半径2,三角形面积公式:面积=底×高÷2,代入数据,即可解答。
【详解】3.14×(3÷2)2÷2+3.14×(4÷2)2÷2+3×4÷2-3.14×(5÷2)2÷2
=3.14×1.52÷2+3.14×22÷2+12÷2+3.14×2.52÷2
=3.14×2.25÷2+3.14×4÷2+6+3.14×6.25÷2
=3.5325+6.28+6-9.8125
=6(平方米)
阴影部分的面积是6平方米。
34.周长为400.96m;面积为9615.36m2
【分析】分析题目,操场的周长等于以32m为半径的圆的周长加2条100m的线段,据此结合圆的周长=2πr列式计算;操场的面积等于以32m为半径的圆的面积加一个以100m为长、圆的直径为宽的长方形的面积,据此结合圆的面积=πr2列式计算即可。
【详解】100×(32×2)
=100×64
=6400(m2)
3.14×322
=3.14×1024
=3215.36(m2)
6400+3215.36=9615.36(m2)
周长:2×32×3.14+100×2
=200.96+200
=400.96(m)
35.19.94平方厘米
【详解】试题分析:根据长方形的面积公式可用36除以4计算出长方形的长为9厘米,空白部分A可看作是一个以9﹣5=4厘米为半径的圆,空白部分B可看作是底为5厘米高为5厘米的三角形,然后根据圆的面积公式和三角形的面积公式计算出A、B的面积,最后再用长方形的面积减去空白部分A的面积再减去空白部分B的面积即可,列式解答即可得到答案.
解:如图,
长方形的长为:45÷5=9(厘米),
空白部分A的面积为:
×3.14×(9﹣5)2=×3.14×16
=12.56(平方厘米),
空白部分B的面积为:
5×5÷2
=25÷2
=12.5(平方厘米),
阴影部分的面积为:
45﹣12.56﹣12.5,
=32.44﹣12.5,
=19.94(平方厘米).
答:阴影部分的面积为19.94平方厘米.
点评:此题主要考查组合图形的面积,其中有长方形、三角形、圆的面积公式及其应用.
36.周长:18.84cm;面积:28.26cm2
【分析】根据圆的周长公式:周长=π×直径,代入数据,求出圆的周长;圆的面积公式:面积=π×半径2,代入数据,求出圆的面积。
【详解】圆的周长:3.14×6=18.84(cm)
圆的面积:3.14×(6÷2)2
=3.14×9
=28.26(cm2)
37.2.86平方厘米;37.68平方厘米
【分析】由图可知阴影部分的面积=长方形的面积-圆的面积,根据长方形的面积公式:长×宽,圆的面积公式:S=πr2即可求解;
由图可知,根据圆环的面积公式:S=π(R2-r2)即可求解。
【详解】3×2-3.14×(2÷2)2
=6-3.14×1
=6-3.14
=2.86(平方厘米)
3.14×(42-22)
=3.14×(16-4)
=3.14×12
=37.68(平方厘米)
38.125.6cm;628cm2
【分析】观察图形可知,两个完全一样的小半圆可以组成一个直径为20cm的圆;则图形的周长=半径是20cm的大圆周长的一半+直径是20cm的小圆的周长,根据圆的周长公式C=2πr或C=πd求解。
把右下方的小半圆移补到左上方的小半圆处,图形正好补成一个半径是20cm的大半圆,则图形的面积=大圆面积的一半,根据圆的面积公式S=πr2求解。
【详解】周长:
2×3.14×20÷2+3.14×20
=62.8+62.8
=125.6(cm)
面积:
3.14×202÷2
=3.14×400÷2
=628(cm2)
图形的周长是125.6cm,面积是628cm2。
39.38.88平方厘米
【分析】先求出直径为8厘米的半圆的面积,再用正方形的面积减去半径为8厘米的圆的面积求出另一个阴影部分的面积,最后将两个阴影部分的面积相加即可。
【详解】8×8- ×3.14×8×8+ ×3.14×(8÷2)
=64-50.24+25.12
=13.76+25.12
=38.88(平方厘米)
40.24平方厘米
【分析】,如图所示,把半圆中右侧的阴影补到左侧空白虚线内,则阴影部分的面积就是长方形的面积减去三角形的面积,据此解答。
【详解】4×8-4×4÷2
=32-8
=24(平方厘米)
41.141.3 cm²
【分析】由图可知阴影部分为圆环,根据圆环的面积公式:即可求解。
【详解】12÷2=6(cm)
=3.14×(81-36)
=3.14×45
=141.3(cm²)
42.周长:22.28dm
面积:37.68dm²
【详解】周长:
6×2+4+3.14×4÷2
=12+4+6.28
=22.28(dm)
面积:
3.14×(4²-2²)
=3.14×(16-4)
=3.14×12
=37.68(dm²)
【点睛】第一个图形的周长包括两条6dm的线段,一条4dm的线段,还有一条直径4dm的半圆弧的长度;圆环面积公式:S=π(R²-r²).
43.9.87dm2
【分析】阴影部分面积=上底是6dm,下底是10dm,高是(6÷2)dm的梯形面积-半径是(6÷2)dm的圆的面积的一半,根据梯形面积公式:面积=(上底+下底)×高÷2,与圆的面积公式:面积=π×半径2,代入数据,即可解答。
【详解】(6+10)×(6÷2)÷2-3.14×(6÷2)2÷2
=16×3÷2-3.14×32÷2
=48÷2-3.14×9÷2
=24-28.26÷2
=24-14.13
=9.87(dm2)
44.9.87cm2
【分析】阴影部分面积=上底是6cm,下底是10cm,高是(6÷2)cm的梯形面积-半径是(6÷2)cm的圆的面积的一半,根据梯形面积公式:面积=(上底+下底)×高÷2,圆的面积公式:面积=π×半径2,代入数据,即可解答。
【详解】(6+10)×(6÷2)÷2-3.14×(6÷2)2÷2
=16×3÷2-3.14×32÷2
=48÷2-3.14×9÷2
=24-28.26÷2
=24-14.13
=9.87(cm2)
45.22.85分米
【分析】根据图可知,这个图形是由一个直径是5分米的半圆弧和3个5分米的边长组成,根据半圆弧的周长公式:C=πd÷2,把数代入即可求解。
【详解】3.14×5÷2+5×3
=7.85+15
=22.85(分米)
46.50.24平方米
【分析】由图可知,把左边正方形中阴影部分移到右边空白三角形上,阴影部分面积正好是一个圆的,用圆的面积×即可。
【详解】3.14×82×
=3.14×64×
=200.96×
=50.24(平方米)
47.13.5平方厘米
【分析】如图:
阴影部分相当于一个上底为(6-3)厘米,下底为6厘米,高为3厘米的梯形,根据梯形的面积=(上底+下底)×高÷2,代入数据解答。
【详解】6-3=3(厘米)
(3+6)×3÷2
=9×3÷2
=13.5(平方厘米)
阴影部分的面积是13.5平方厘米。
48.
【分析】根据题意,把阴影部分通过转移,分解成下图,,阴影部分面积就是直径4厘米的半圆面积减去底是4厘米,高是(4÷2)厘米的三角形面积,根据圆的面积公式:π×半径2,三角形面积公式:底×高÷2,代入数据,即可解答。
【详解】3.14×(4÷2)2÷2-4×(4÷2)÷2
=3.14×4÷2-4×2÷2
=12.56÷2-8÷2
=6.28-4
=2.28(cm2)
49.面积:100.48平方厘米;周长:132.48厘米
【分析】由图可以看出,阴影部分的面积等于大圆的面积减去圆内四个空白部分拼成的2个直径为8cm的小圆的面积;阴影部分的周长等于大圆的周长加上一个直径为8cm的小圆的周长,再加上4个大圆的半径;圆的面积公式S=πr2,圆的周长=2πr。据此计算。
【详解】
=3.14×64-3.14×32
=3.14×(64-32)
=3.14×32
=100.48(平方厘米)
=3.14×16+3.14×16+32
=3.14×(16+16)+32
=100.48+32
=132.48(厘米)
50.25.12dm2
【分析】阴影部分面积等于半径是8dm圆的面积的减去半径是(8÷2)dm圆的面积的一半,根据圆的面积公式:面积=π×半径2,代入数据,即可解答。
【详解】3.14×82×-3.14×(8÷2)2÷2
=3.14×64×-3.14×42÷2
=200.96×-3.14×16÷2
=50.24-50.24÷2
=50.24-25.12
=25.12(dm2)
51.50.24cm²;114cm²;7.74dm²
【分析】(1)圆环的面积=大圆的面积-小圆的面积;
(2)阴影部分的面积=圆的面积-底是20厘米,高是10厘米的两个三角形的面积;
(3)阴影部分的面积=正方形的面积- ×圆的面积。
【详解】(1)3.14×(10÷2)2-3.14×(6÷2)2
=78.5-28.26
=50.24(cm²)
(2)3.14×(20÷2)2-20×(20÷2)÷2×2
=314-200
=114(cm²)
(3)6×6- ×3.14×62
=36-28.26
=7.74(dm²)
【点睛】此题主要考查含圆的阴影部分面积的计算,找出阴影部分与图形之间的关系是解题关键。
52.周长102.8分米;面积400平方分米
【分析】根据图可知,阴影部分的周长,相当于空白部分的半圆弧和阴影部分的半圆弧的长度加上两个正方形的边长,由于两个半圆弧的直径都是20分米,由此即可知道这两个半圆弧周长相等,根据半圆弧的周长公式:C=πd÷2,把数代入即可求解;
由于阴影部分的半圆和空白部分的半圆直径相同,由此即可知道面积相等,那么可知阴影部分的面积=正方形的面积,根据正方形的面积公式:边长×边长,即可解答。
【详解】周长:3.14×20÷2×2+20×2
=62.8÷2×2+40
=62.8+40
=102.8(分米)
面积:20×20=400(平方分米)
53.21.5平方厘米;25.12平方厘米
【分析】(1)4个空白扇形组成一个整圆,阴影部分的面积=正方形的面积-圆的面积,根据正方形面积=边长×边长,圆的面积=π即可解答。
(2)4个相同的半圆组成两个整圆,根据圆的面积=π求出一个圆的面积,再乘2即可解答.
【详解】(1)10×10-3.14×
=100-78.5
=21.5(平方厘米)
(2)3.14××2
=3.14×4×2
=25.12(平方厘米)
【点睛】本题考查含圆的阴影部分的面积,明确阴影部分的组成是解题的关键。
54.41.42厘米
【分析】观察图形发现,阴影部分的周长是4个半径4厘米的四分之一圆弧的周长,即一个半径4厘米的圆的周长,加上一个边长是4厘米的正方形的周长,代入数据计算即可。
【详解】3.14×4×2+4×4
=25.12+16
=41.12(厘米)
55.144.5平方厘米
【解析】略
56.24平方厘米
【分析】在图中画一条辅助线,如下图所示。观察图形可知:A1的面积=A2的面积,则阴影部分的面积=长方形的面积-左边三角形的面积。长方形的面积=长×宽,三角形的面积=底×高÷2,据此解答。
【详解】8×4=32(平方厘米)
4×4÷2=8(平方厘米)
32-8=24(平方厘米)
57.111.4米;30.84米
【分析】组合图形的周长=直径是10米的圆的周长+2个40米;半圆的周长=圆周长的一半+圆的直径;
【详解】3.14×10+40×2
=31.4+80
=111.4(米)
3.14×12÷2+12
=18.84+12
=30.84(米)
58.114cm2
【分析】阴影部分的面积=圆的面积-正方形的面积,代入数据计算即可。
【详解】3.14×102-10×2×10÷2×2
=3.14×100-100×2
=314-200
=114(cm2)
(期末典型真题)图形综合计算-广东省深圳市2023-2024学年五年级上册数学期末真题精选(北师大版): 这是一份(期末典型真题)图形综合计算-广东省深圳市2023-2024学年五年级上册数学期末真题精选(北师大版),共25页。试卷主要包含了看图列式,图形计算等内容,欢迎下载使用。
(期末典型真题)图形计算-广东省深圳市2023-2024学年五年级上册数学期末真题精选(北师大版): 这是一份(期末典型真题)图形计算-广东省深圳市2023-2024学年五年级上册数学期末真题精选(北师大版),共28页。试卷主要包含了计算下面各图形的面积,计算如图图形的面积,计算下面图形中涂色部分的面积,计算所示图形的面积,计算下面图形的面积,计算下列图形的面积,求平行四边形中阴影部分的面积,求下面三角形的面积等内容,欢迎下载使用。
(期末典型真题)作图题-广东省深圳市2023-2024学年六年级上册数学期末真题精选(北师大版): 这是一份(期末典型真题)作图题-广东省深圳市2023-2024学年六年级上册数学期末真题精选(北师大版),共24页。试卷主要包含了在下面的图中涂出对应的百分数,按要求把下列的方格图补充完整等内容,欢迎下载使用。













