初中数学北师大版八年级下册2 平行四边形的判定说课ppt课件

这是一份初中数学北师大版八年级下册2 平行四边形的判定说课ppt课件，共18页。PPT课件主要包含了学习目标，导入新课，平行四边形判定定理，复习引入，讲授新课，合作探究，OAOC已知，OBOD已知，∵AOCO，BODO等内容，欢迎下载使用。

1.利用对角线互相平分判定平行四边形;（重点）
2.平行四边形对角线相等的相关运用.（难点）
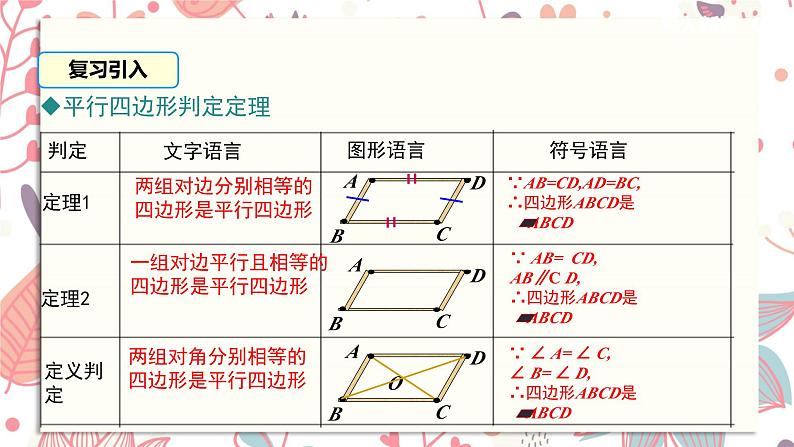
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
∵AB=CD,AD=BC,∴四边形ABCD是 ABCD
∵ AB= CD, AB∥C D,∴四边形ABCD是 ABCD
∵ ∠ A= ∠ C, ∠ B= ∠ D,∴四边形ABCD是 ABCD
将两根木条AC，BD的中点重叠，并用钉子固定，再用一根橡皮筋绕端点A，B，C，D围成一个四边形ABCD ．想一想，△AOB≌△COD吗？四边形ABCD的对边之间有什么关系？你得到什么结论？
猜想：对角线互相平分的四边形是平行四边形.
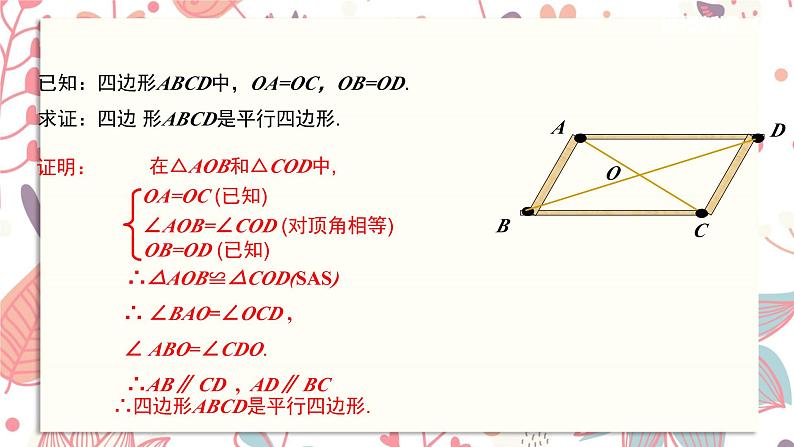
已知：四边形ABCD中，OA=OC，OB=OD.求证：四边 形ABCD是平行四边形.
在△AOB和△COD中,
∠AOB=∠COD (对顶角相等)
∴△AOB≌△COD(SAS)
∴ ∠BAO=∠OCD , ∠ ABO=∠CDO.
∴AB∥ CD , AD∥ BC
∴四边形ABCD是平行四边形.
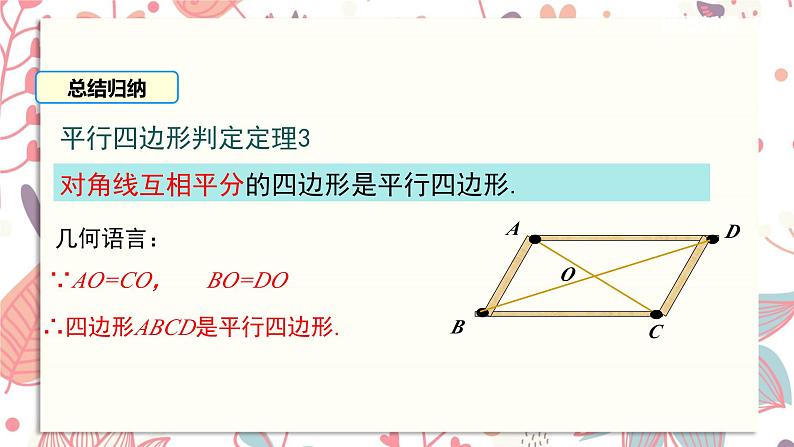
对角线互相平分的四边形是平行四边形.
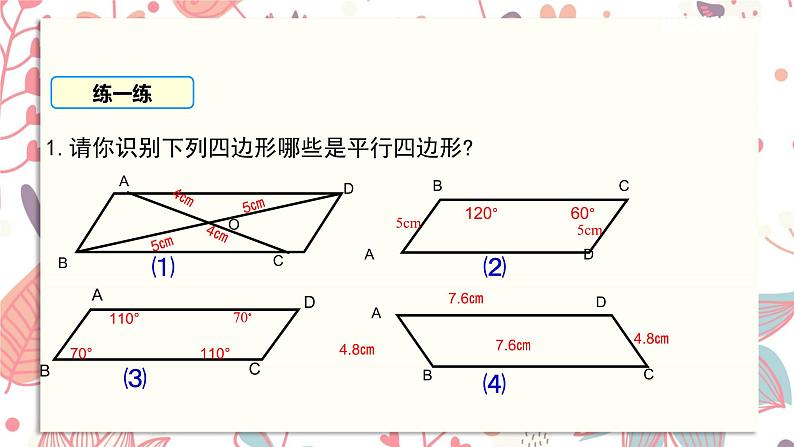
1.请你识别下列四边形哪些是平行四边形?
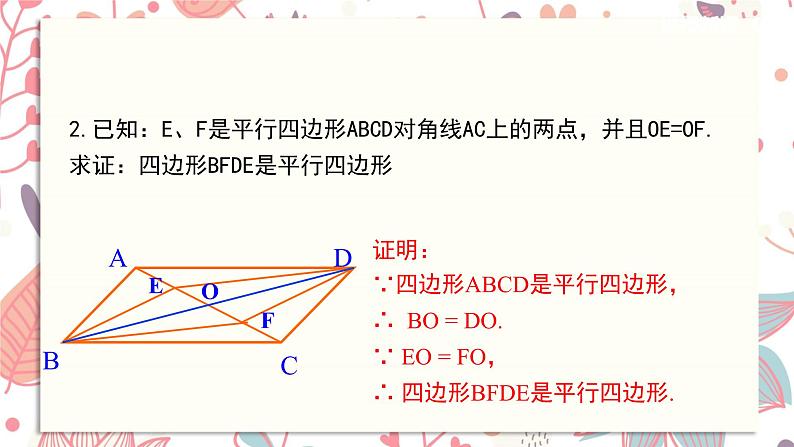
2.已知：E、F是平行四边形ABCD对角线AC上的两点，并且OE=OF.求证：四边形BFDE是平行四边形
证明： ∵四边形ABCD是平行四边形，∴ BO = DO.∵ EO = FO，∴ 四边形BFDE是平行四边形.
例1 已知：E、F是平行四边形ABCD对角线AC上的两点，并且AE=CF.求证：四边形BFDE是平行四边形.
在ABCD中，AO=CO，BO=DO
∴AO-AE=CO-CF
又 ∵BO=DO
∴ 四边形BFDE是平行四边形.
(对角线互相平分的四边形是平行四边形）
（4）如图， □ABCD 的对角线AC,BD相交于点O,E,F是AC上的两点，补充条件： ,使得四边形BFDE是平行四边形.
证明：∵四边形ABCD是平行四边形，
∴ AO=CO,BO=DO.
∴ AO-AE=CO-CF,即EO=OF.
∴四边形BFDE是平行四边形.
想一想：判定一个四边形是平行边形可以从哪些角度思考?具体有哪些方法?
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理1)
一组对边平行且相等的四边形是平行四边形（判定定理2）
两组对角分别相等的四边形是平行四边形（定义拓展）
对角线互相平分的四边形是平行四边形（判定定理3）
小明用手中六个全等的正三角形做拼图游戏时，拼成一个六边形．你能在图中找出所有的平行四边形吗？并说说你的理由．
解：有6个平行四边形，分别是：　 ABOF， ABCO， BCDO， CDEO， DEFO， EFAO．
1. 根据下列条件，不能判定一个四边形为平行四边形的是（ ）
A. 两组对边分别相等
B . 两条对角线互相平分
C . 两条对角线相等
D . 两组对边分别平行
3.已知：如图，在四边形ABCD中，AB∥CD，E是BC的中点，直线AE交DC的延长线于点F．试判断四边形ABFC的形状，并证明你的结论．
∴△ABE≌△FCE（AAS）； ∴AE=EF，又∵BE=CE∴四边形ABFC是平行四边形．
解：四边形ABFC是平行四边形；理由如下：∵AB∥CD，∴∠BAE=∠CFE，∵E是BC的中点，∴BE=CE，在△ABE和△FCE中，