浙教版七年级下册3.4 乘法公式多媒体教学ppt课件

这是一份浙教版七年级下册3.4 乘法公式多媒体教学ppt课件，共18页。PPT课件主要包含了算一算，4x2，a+b2，x+y2，3xy2，合作学习，完全平方公式，3a+225，a−b2，想一想等内容，欢迎下载使用。

观察上述1、2两题的计算结果，你发现有什么规律？
=(a+b)(a+b)
=(x+y)(x+y)
两数和的平方,等于这两数的平方和 , 加上这两数积的2倍.
(a+b)2=a2+2ab+b2
首平方，尾平方，首尾两倍放中央.
利用完全平方公式简便计算：
例1 运用完全平方公式计算：
(1)(x+2y)2 (2)(2a+5)2
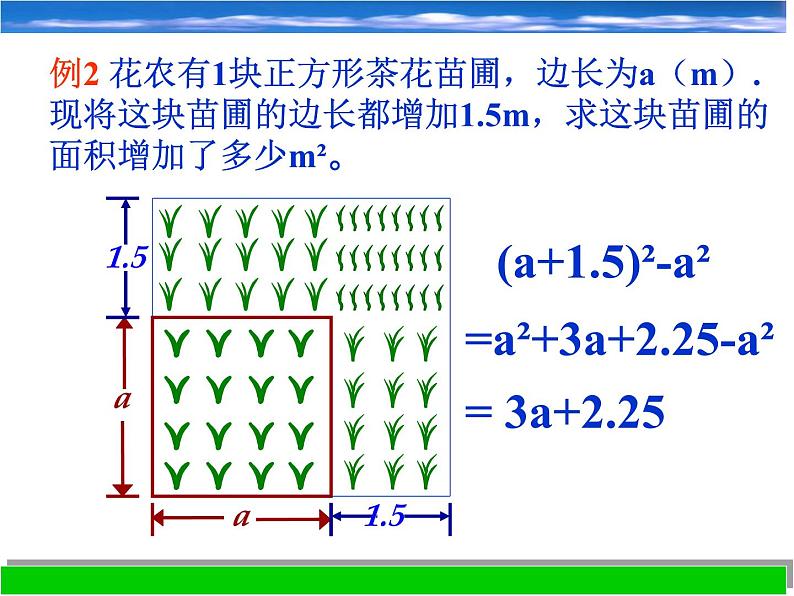
例2 花农有1块正方形茶花苗圃，边长为a（m）.现将这块苗圃的边长都增加1.5m，求这块苗圃的面积增加了多少m²。
(a+1.5)²-a²
=a²+3a+2.25-a²
a2 −2ab+b2.
= a2 +2a(-b)+ (−b)2= a2 –2ab+ b2
在横线上填入适当的整式:
1、下面各式的计算是否正确？如果不正确，应当怎样改正？
(2)(x -y)2 =x2 -y2
(3) (x -y)2 =x2-2xy -y2
(4) (x+2y)2 =x2 +2xy +2y2
(x +y)2 =x2+2xy +y2
(x -y)2 =x2 -2xy +y2
(x +2y)2 =x2+4xy +4y2
（1）(x+y)2=x2 +y2
(2) (a-2 b)2 与 (2b - a)2
(1) (-a-b)2 与(a+b)2
2、比较下列各式之间的关系：
（3）(-3b +2a)2 与(-2a +3b)2
互为相反数的两式的完全平方结果一样。
3． 下列等式是否成立? 说明理由．(1) (4a+1)2=(1−4a)2； (2) (4a−1)2=(4a+1)2；(3) (4a−1)(1−4a)＝(4a−1)(4a−1) ＝(4a−1)2；(4) (4a−1)(1−4a)＝(4a−1)(4a+1).
灵活应用一 利用完全平方公式计算：(1) 0.982 (2) 10012
解：(1) 原式 = （ 1 − 0.02）2
= 12 − 2 ×1×0.02 + 0.022
= 1 − 0.04 + 0.0004
（2）原式 = （ 1000 + 1 ）2
= 10002 + 2 × 1000×1 + 12
= 1000000 + 2000 + 1
(1)如果x2+ax+36是一个完全平方式,那么a=______
(3)已知(a+b)2=11,ab=1,求(a-b)2的值.
(2)如果x2+6x+b2是一个完全平方式,那么b= ；