高中数学人教A版 (2019)必修 第二册第八章 立体几何初步8.2 立体图形的直观图同步训练题

这是一份高中数学人教A版 (2019)必修 第二册第八章 立体几何初步8.2 立体图形的直观图同步训练题，共9页。试卷主要包含了下面的说法正确的是，5 cm，2 cm，0等内容，欢迎下载使用。

1.下面的说法正确的是( )
A．水平放置的正方形的直观图可能是梯形
B．两条相交直线的直观图可能是平行直线
C．互相垂直的两条直线的直观图仍然互相垂直
D．平行四边形的直观图仍然是平行四边形
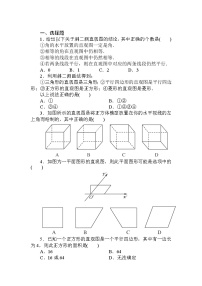
2．下列直观图是将正方体模型放置在你的水平视线的左下角而绘制的是( )
3．如图，B′C′∥x′轴，A′C′∥y′轴，则下面直观图所表示的平面图形是( )
A．正三角形 B．锐角三角形
C．钝角三角形 D．直角三角形
4．已知一个建筑物上部为四棱锥，下部为长方体，且四棱锥的底面与长方体的上底面尺寸一样，长方体的长、宽、高分别为20 m，5 m，10 m，四棱锥的高为8 m．如果按1∶500的比例画出它的直观图，那么在直观图中，长方体的长、宽、高和棱锥的高应分别为( )
A．4 cm，1 cm，2 cm，1.6 cm
B．4 cm，0.5 cm，2 cm，0.8 cm
C．4 cm，0.5 cm，2 cm，1.6 cm
D．4 cm，0.5 cm，1 cm，0.8 cm
5.
(多选)如图，已知等腰三角形ABC，则如下所示的四个图中，可能是△ABC的直观图的是( )
6．(多选)画水平放置的圆的直观图时，下列说法中正确的有( )
A．每条直径的大小都发生了改变
B．必有两条直径相等
C．每条直径都比实际的短
D．直观图的面积比原图形的面积小
7．如图所示为一个平面图形的直观图，则它的原图形四边形ABCD的形状为________．
8．如图，△A′O′B′是用斜二测画法得到的△AOB的直观图，其中O′A′＝2，O′B′＝3，则AB的长度为________．
9．用斜二测法画出如图边长为2 cm的等边三角形的直观图，并求直观图面积．
10.
如图，一个水平放置的平面图形的直观图是一个底角为45°，腰和上底长均为1的等腰梯形，求原图形的面积．
能力提升
11.一个三角形水平放置的直观图是正三角形，则原三角形是( )
A．正三角形 B．直角三角形
C．钝角三角形 D．以上都有可能
12.
如图所示的水平放置的三角形的直观图，D′是△A′B′C′中B′C′边的中点，且A′D′平行于y′轴，那么A′B′，A′D′，A′C′三条线段对应原图形中线段AB，AD，AC中( )
A．最长的是AB，最短的是AC
B．最长的是AC，最短的是AB
C．最长的是AB，最短的是AD
D．最长的是AD，最短的是AC
13．已知正方形ABCD的边长为a，按照斜二测画法作出它的直观图A′B′C′D′，直观图面积为 eq \r(2)，则a值为( )
A．6 eq \r(3) B．2C．1 D． eq \r(3)
14.
(多选)如图所示，△A′B′C′是水平放置的△ABC的斜二测直观图，其中O′C′＝O′A′＝2O′B′＝2，则以下说法正确的是( )
A．△ABC是钝角三角形
B．△ABC的面积是△A′B′C′的面积的2倍
C．△ABC是等腰直角三角形
D．△ABC的周长是4＋4 eq \r(2)
[答题区]
15.
在如图所示的直观图中，四边形O′A′B′C′为菱形且边长为2 cm，则在平面直角坐标系中原四边形OABC为________(填具体形状)，其面积为________ cm2.
16．在直四棱柱ABCD ­A1B1C1D1中，AB∥CD，∠DAB＝90°，AB＝2，CD＝1，AD＝3，AA1＝4.
(1)画出四棱柱ABCD ­A1B1C1D1的直观图；
(2)将四棱柱ABCD ­A1B1C1D1补成一个长方体，并说出补上的几何体的名称．
课时作业23 立体图形的直观图
1．解析：由直观图的画法平行性不变，故A和B错误，D正确；而C中由于在直观图中x′和y′所成角为45°或135°，故C错误．故选D.
答案：D
2．解析：由题意知，应看到正方体的上面、前面和右面，由几何体直观图的画法及直观图中虚线的使用，可知选A.
答案：A
3．解析：
因为B′C′∥x′轴，A′C′∥y′轴，所以复原原图即平面图中BC∥x轴，AC∥y轴，所以三角形是直角三角形．故选D.
答案：D
4．解析：由比例尺可知，长方体的长、宽、高和棱锥的高分别为4 cm，1 cm，2 cm和1.6 cm，再结合直观图，知在直观图中，长方体的长、宽、高和棱锥的高应分别为4 cm，0.5 cm，2 cm，1.6 cm.故选C.
答案：C
5．解析：原等腰三角形画成直观图后，原来的腰长不相等，CD两图分别为在∠x′O′y′成135°和45°的坐标系中的直观图．故选CD.
答案：CD
6．解析：由斜二测画法可知，与x轴平行或重合的直径长度不变，故AC错误；由图可知，D正确；由图可知，当点P′由点A′沿曲线向点B′运动时，过点P′的直径先减后增，由对称性知，所以必有两条直线相等，故B正确．故选BD.

答案：BD
7.
解析：因为∠D′A′B′＝45°，由斜二测画法的规则知∠DAB＝90°，又因为四边形A′B′C′D′为平行四边形，且A′B′＝2B′C′，所以AB＝BC＝2，且DC∥AB，DC＝AB，所以原四边形ABCD为正方形．
答案：正方形
8．解析：把直观图△A′O′B′还原为△AOB，如图所示：
根据直观图画法规则知，OA＝O′A′＝2，OB＝2O′B′＝2×3＝6，所以AB的长度为AB＝ eq \r(OA2＋OB2)＝ eq \r(4＋36)＝2 eq \r(10).
答案：2 eq \r(10)
9．解析：画法：(1)如图①，在等边三角形ABC中，取BC所在直线为x轴，BC的垂直平分线为y轴，两轴相交于点O.在图②中，画相应的x′轴与y′轴，两轴相交于点O′，使∠x′O′y′＝45°.
(2)在图②中，以O′为中点，在x′轴上取B′C′＝BC，在y′轴上取O′A′＝ eq \f(1,2)OA.
(3)连接A′B′，A′C′，并擦去辅助线x′轴和y′轴，便获得等边三角形ABC水平放置的直观图A′B′C′(图③).
由题意在平面直角坐标系中，三角形ABC是边长为2的正三角形，
∴AB＝BC＝2 cm，BC边上的高为h＝ eq \r(3) cm，
在三角形A′O′C′中，∠A′O′C′＝45°，
∴B′C′＝BC＝2 cm，A′O′＝ eq \f(1,2)AO＝ eq \f(\r(3),2) cm，
B′C′边上的高h′＝A′O′sin ∠A′O′C′＝ eq \f(\r(3),2)× eq \f(\r(2),2)＝ eq \f(\r(6),4)(cm)，
故S△A′B′C′＝ eq \f(1,2)B′C′·h′＝ eq \f(1,2)×2× eq \f(\r(6),4)＝ eq \f(\r(6),4)(cm2)，
故直观图△A′B′C′面积为 eq \f(\r(6),4) cm2.
10．解析：一个水平放置的平面图形的直观图是一个底角为45°，腰和上底长均为1的等腰梯形，
所以其直观图的面积S′＝ eq \f(1,2)×(1＋1＋ eq \r(2))× eq \f(\r(2),2)＝ eq \f(\r(2)＋1,2).
可得原平面图形的面积S＝ eq \f(S′,\f(\r(2),4))＝2＋ eq \r(2).
11.
解析：令正△O′A′B′是水平放置的△OAB的直观图，不妨令点A′在数轴O′x′上，如图，
因为∠y′O′x′＝45°，则线段A′B′与y′轴必相交，令交点为C′，
在直角坐标系xOy中，点A在x轴上，OA＝O′A′，点C在y轴上，OC＝2O′C′，如图，
因此点B必在线段AC的延长线上，有∠BOA>∠COA＝90°，即△OAB是钝角三角形，
所以原三角形是钝角三角形．故选C.
答案：C
12．解析：
如图，因为A′D′∥y′轴，所以在△ABC中，AD⊥BC，又因为D′是B′C′的中点，所以D是BC中点，所以AB＝AC>AD.故选C.
答案：C
13．解析：以A为原点，以AB和AD所在的直线分别为x轴、y轴建立平面直角坐标系，如图(1)所示．根据斜二测画法的规则，得到边长为a的正方形的直观图，如图(2)所示．因为AB＝AD＝a，可得A′B′＝a，A′D′＝ eq \f(a,2)，又因为∠x′O′y′＝45°，过D′作D′E′⊥A′B′，可得D′E′＝ eq \f(a,2)×sin 45°＝ eq \f(\r(2)a,4)，由直观图A′B′C′D′的面积为 eq \r(2)，所以a× eq \f(\r(2)a,4)＝ eq \r(2)，解得a＝2.故选B.
答案：B
14．解析：根据斜二测画法可知，在原图形中，O为CA的中点，AC⊥OB，
因为O′C′＝O′A′＝2O′B′＝2，所以CO＝AO＝2，AC＝4，OB＝2，则△ABC是斜边为4的等腰直角三角形，如图所示，所以△ABC的周长是4＋4 eq \r(2)，面积是4，故A错误，C，D正确；由斜二测画法可知，△ABC的面积是△A′B′C′的面积的2 eq \r(2)倍，故B错误．故选CD.
答案：CD
15．解析：由斜二测画法规则可知，在四边形OABC中，OA⊥OC，OA＝O′A′＝2 cm，OC＝2O′C′＝4 cm，所以四边形OABC是矩形，其面积为2×4＝8(cm2).
答案：矩形 8
16．解析：(1)由题意，结合直观图的画法，即可得到四棱柱ABCD ­A1B1C1D1的直观图如图①.
(2)由题意，结合长方体的几何特征，可得补成的长方体如图②，
即补上的几何体是三棱柱BCE ­B1C1E1.

题号
1
2
3
4
5
6
11
12
13
14
答案