黑龙江省哈尔滨市第四十七中学2023-2024学年七年级上学期期中数学试题

这是一份黑龙江省哈尔滨市第四十七中学2023-2024学年七年级上学期期中数学试题，共5页。试卷主要包含了单选题，填空题，未知，解答题等内容，欢迎下载使用。


一、单选题
1．下列等式中是一元一次方程的是（ ）
A．B．C．D．
2．根据等式的基本性质，下列结论正确的是（ ）
A．若，则B．若，则
C．若，则D．若，则
3．解一元一次方程，移项正确的是（ ）
A．B．
C．D．
4．方程去分母后，正确的是（ ）
A．B．
C．D．
5．某个体商贩在一次买卖中，同时卖出两件上衣，售价都是135元，若按成本计，其中一件盈利25％，另一件亏本25％，在这次买卖中他（ ）．
A．不赚不赔B．赚9元C．赔18元D．赚18元
6．下列图中，和是对顶角的是（ ）
A． B．
C． D．
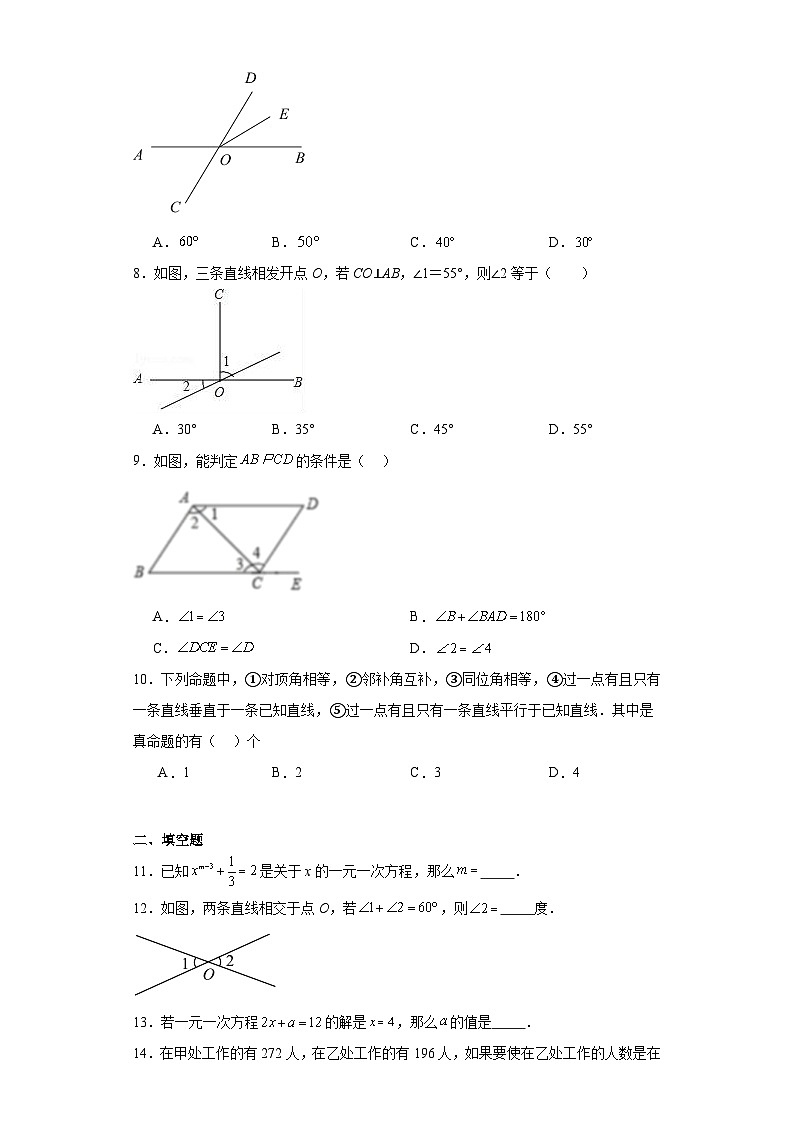
7．如图，直线、相交于点O，平分，若，则（ ）
A．B．C．D．
8．如图，三条直线相发开点O，若CO⊥AB，∠1＝55°，则∠2等于（ ）
A．30°B．35°C．45°D．55°
9．如图，能判定的条件是（ ）
A．B．
C．D．
10．下列命题中，①对顶角相等，②邻补角互补，③同位角相等，④过一点有且只有一条直线垂直于一条已知直线，⑤过一点有且只有一条直线平行于已知直线．其中是真命题的有（ ）个
A．1B．2C．3D．4
二、填空题
11．已知是关于x的一元一次方程，那么 ．
12．如图，两条直线相交于点O，若，则 度．
13．若一元一次方程的解是，那么的值是 ．
14．在甲处工作的有272人，在乙处工作的有196人，如果要使在乙处工作的人数是在甲处工作人数的，那么应从乙处调出 人到甲处．
15．当 时，代数式与的值相反．
16．如图，某住宅小区内有一长方形地，若在长方形地内修筑同样宽的小路（图中阴影都分），余下部分绿化，小路的宽均为，则绿化的面积为 .

17．已知和，两个角的两边分别平行，，则的大小为 ．
18．已知：如图，，的平分线与的平分线交于点M，，，，则 ．
三、未知
19．解方程：
(1)
(2)
20．如图，在边长为1个单位的正方形网格中，经过平移后得到，图中标出了点B的对应点．根据下列条件，利用网格点和无刻度的直尺画图．
(1)画出；
(2)直接写出三角形的面积．
21．推理填空：如图：，．求证：．
证明：因为（已知），（____________），
得，
所以（____________），
得，
因为（已知），
得（等量代换），
所以（____________），
所以（____________）．
22．若关于x的一元一次方程化成后的解满足，则称该方程为“绝配方程”，例如：方程的解为，而，则方程为“绝配方程”．
(1)①，②，③三个方程中，为“绝配方程”的是______（填写序号）；
(2)若关于x的一元一次方程化成后是“绝配方程”，求m的值．
四、解答题
23．已知：如图，直线与直线交点O，，平分．
(1)如图1，求证：平分；
(2)如图2，，在直线的下方，若平分，平分，，求的度数．
五、未知
24．某工厂一车间有名工人，某月接到加工两种轿车零件的生产任务．每个工人每天能加工甲种零件个，或加工乙种零件个．
(1)若一辆轿车只需要甲零件1个和乙零件1个使每天能配套生产轿车，问应安排多少工人加工甲种零件？
(2)若一辆轿车需要甲零件7个和乙零件2个使每天能配套生产轿车，若加工一件甲种零件加工费为元，加工一件乙种零件加工费为元，若名工人正好使得每天加工零件能配套生产轿车，求一天这名工人所得加工费一共多少元？
25．已知：如图，，直线分别交于点G，H，点P为直线上的点，连接．

(1)如图1，点P在线段上时，请你直接写出，，的数量关系；
(2)如图2，点P在的延长线上时，连接交于点Q，连接，若，求证：；
(3)在（2）的条件下，如图3，平分，平分，与交点K，连接，若，，，求的大小．