辽宁省葫芦岛市龙港区2023-2024学年九年级上学期第一次月考数学试题

这是一份辽宁省葫芦岛市龙港区2023-2024学年九年级上学期第一次月考数学试题，共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
本试卷共25道题 考试时间共120分钟 试卷满分120分
※考生注意：请在答题卡各题目规定答题区域内作答，答在本试卷上无效．
一、选择题（本题共10小题，每题2分，共20分）
1．下列方程中，是一元二次方程的是（ ）
A． B． C． D．
2．把方程化成的形式，则的值分别为（ ）
A．3，1，4 B．3，，4 C．3，，4 D．3，4，
3．将抛物线向右平移2个果位长度，再向上平移3个单位长度，所得的抛物线是（ ）
A． B． C． D．
4．某种新型礼炮的升空高度飞行时间的关系式是，若这种礼炮在点火升空到最高点处引爆，则从点火升空到引爆需要的时间为（ ）
A． B． C． D．
5．函数的图象与轴有交点，则的取值范围是（ ）
A． B．且 C． D．且
6．由下表估算一元二次方程的一个近似解的范围为（ ）
A． B． C． D．
某品牌网上专卖店1月份的营业额为60万元，已知第二季度的总营亚额共360万元，如果平均每月增长率为，则由题意列方程应为（ ）
A． B．
C． D．
8．若点都是二次函数的图象上的点，则（ ）
A． B． C． D．
9．在同一平面直角坐标系中，二次函数和一次函数的图象大致是（ ）
A． B．
C． D．
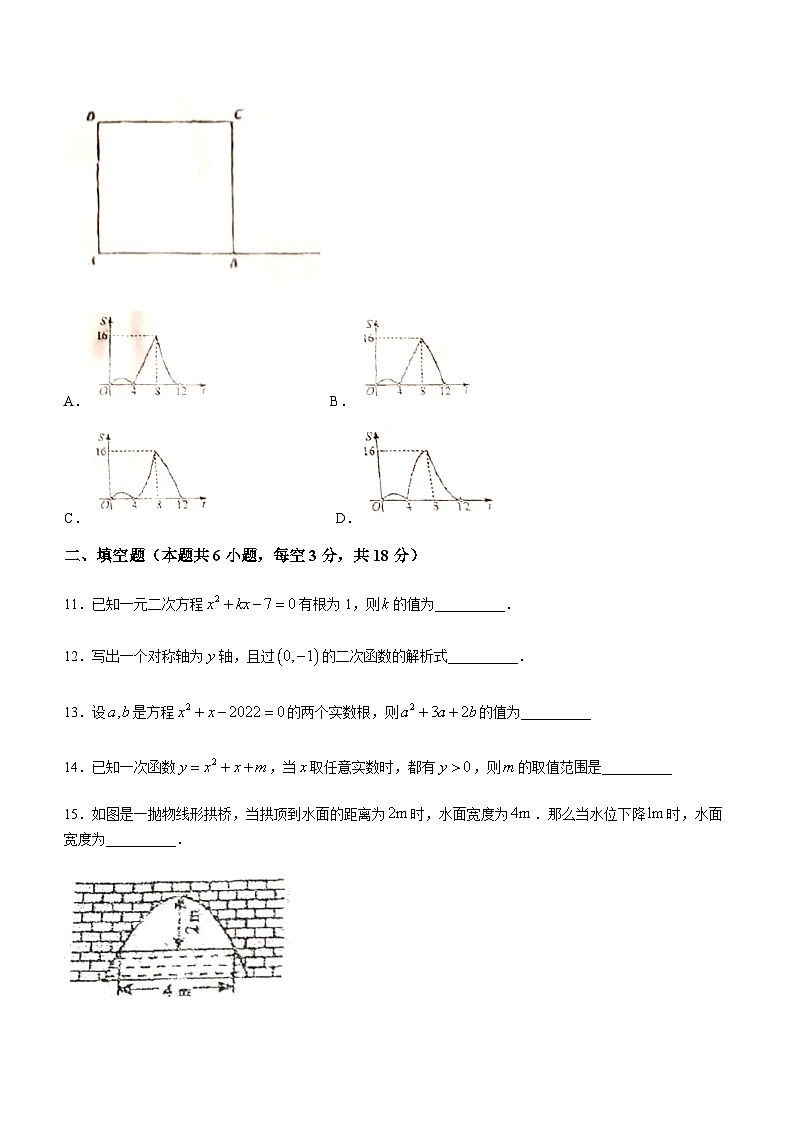
10．如图，正方形的边长为，点从点出发，以每秒的速度沿折线匀速运动，同时点从点出发，以相同的速度沿射线方向匀速运动，过点作于点．当点停止运动时，点也停止运动．设的面积为，运动时间为秒，且，则能反映与的函数关系的图象是（ ）．
A． B．
C． D．
二、填空题（本题共6小题，每空3分，共18分）
11．已知一元二次方程有根为1，则的值为__________．
12．写出一个对称轴为轴，且过的二次函数的解析式__________．
13．设是方程的两个实数根，则的值为__________
14．已知一次函数，当取任意实数时，都有，则的取值范围是__________
15．如图是一抛物线形拱桥，当拱顶到水面的距离为时，水面宽度为．那么当水位下降时，水面宽度为__________．
16．二次函数的部分图像如图，图像过点，对称轴为直线，下列结论：①；②；③④；⑤当时，的值随值的增大而增大．其中正确的结论有__________
三、解答题（本题共7小题，共82分）
17．（本题6分，每小题3分）解下列各方程
（1）（配方法）；
（2）
18．（本题8分）已知关于的方程有两个不相等的实数根．
（1）若为正整数求的值
（2）若满足，求的值．
19．（本题8分）先化简，再求值，其中满足
20．（本题8分）已知：二次函数
（1）用配方法将函数关系式化为形式，并指出数图象的对称轴和顶点坐标；
（2）画出所给函数的图象；
（3）观察图象，指出当时的取值范围．
21．（本题8分）某农场要建一个饲养场（长方形），饲养场的一面靠墙（墙最大可用长度为27米），另三边用木栏围成，中间也用木栏隔开，分成两个场地，并在如图所示的三处各留1米宽的门（不用木栏），建成后木栏总长57米，设饲养场（长方形）的宽为米
（1）饲养场的长为__________米（用含的代数式表示）
（2）若饲养场的面积为，求的值．
22．（本题10分）如图，抛物线与轴交于两点，与轴交于点．已知点的坐标是，抛物线的对称轴是直线．
（1）直接写出点的坐标；
（2）在对称轴上找一点，使的值最小，求点的坐标．
（3）当时最大值为时，直接写出的值．
23．（本题10分）某超市销售一款洗手液，其成本价为每瓶16元，当销售单价定为20元时，每天可售出80瓶．根据市场行情，现决定降价销售．市场调查反映：销售单价每降低0.5元，则每天可多售出20瓶（销售单价不低于成本价），若设这款的销售单价为（元），每天的销售量为（瓶）
（1）写出每天的销售量（瓶）与销售单价（元）之间的函数关系式；
（2）销售这款“洗手液”每天的最大利润为多少元？
24．（本题12分）如图，在等腰中，，，动点以的速度从点出发，沿边向终点运动，过作于点，以为邻边作平行四边形，设点的运动时间为，平行四边形与重叠部分图形面积为．
（I）当点落在边上时，求的值；
（2）求与的函数关系，并直接写出自变量的取值范围．
25．（本题12分）如图，抛物线经过两点，与轴交于点，直线经过点，与轴交于点．
备用图
（1）求抛物线的解析式；
（2）将在直线上平移，平移后的三角形记为，直线交抛物线于，当时，求点的坐标；
（3）若点在轴上，点在抛物线上，是否存在以为顶点且以为一边的平行四边形？若存在，直接写出点的坐标；若不存在，请说明理由．
参考答案
1．B 2．B 3．C 4．B 5．C 6．C 7．B 8．B 9．B 10．B 11．6 12．（答案不唯一） 13．2020 14． 15． 16．①③④
17．（1）；
（2）．
18．解：（1）∵关于的方程有两个不相等的实数根
．
解得：，
为正整数，
或2；
（2），
，
，
即，
解得：，
．
19．解：
（1）原式；
（2）满足
解得：，
当时，原式．
20．解：（1），
∴该抛物线的对称轴是，顶点坐标是；
（2）由抛物线解析式列表，
所以其图象如图所示：
（3）根据图象知，当时，．
21．（1）；
（2）由题意得：，
整理得，
解得；
当时，，
故不合题意，舍去，
当时，，
则；
答：的值为12．
22．解：（1）∵抛物线的对称轴是直线，
，即①，
∵抛物线与轴交于两点，点的坐标是，
②，
联立①②得，
解得
∴二次函数解析式为．
令得，，
解得；
∴点的坐标为；
（2）∵点关于直线对称，
，
设直线解析式为，
将代入得
解得，
∴直线解析式为，
当时，，
；
（3）或．
23．解：（1）根据题意知，
∴每天的销售量（瓶）与销售单价（元）之间的函数关系式；
（2）设每月销售利润为元，则
，
，∴开口向下，
，解得，
，
∴当时，有最大值，最大值为360元．
答：当售价为19元时，每月销售利润最大，最大利润是360元．
24．解：为等腰直角三角形，，
，
，
，
，
．
，
，
，
∵四边形为平行四边形，
，
当点在边上时，如图1，
，
．
，
为等腰直角三角形，
，
，
，
，
．
图1
（2）解：①当时，如图2，
；
图2
②∵在中，．
，
，
∴当时，如图3，分别交于点、点，
，
，
为等腰直角三角形，
．
，
，
，
，
为等腰直角三角形，
，
，
综上所述，
图3
25．（1）解：抛物线经过两点，
，解得，，
∴抛物线的解析式为．
（2）解：直线经过点，且，
，解得，，
∴直线的解析式为，
，
是等腰直角三角形，
将在直线上平移，设向右平移个单位，则向上平移为个单位，
∴点的对应点的坐标为，直线交抛物线于，则，
当点在点下方时，，且，
，解得，，
∴点的坐标为或；
当点在点上方时，，且，
，解得，，
∴点的坐标为或；
综上所述，点的坐标为或或或．
（3）点坐标为或或或…
1.2
1.3
1.4
1.5
1.6
…
…
11.84
12.29
12.76
13.25
13.76
…
…
0
1
…
…
2.5
4
4.5
4
2.5
…