人教版数学七年级下册【单元测试】第五章相交线与平行线(A卷)含解析答案
展开【单元测试】第五章 相交线与平行线(A卷)
学校:___________姓名:___________班级:___________考号:___________
| 一、单选题 |
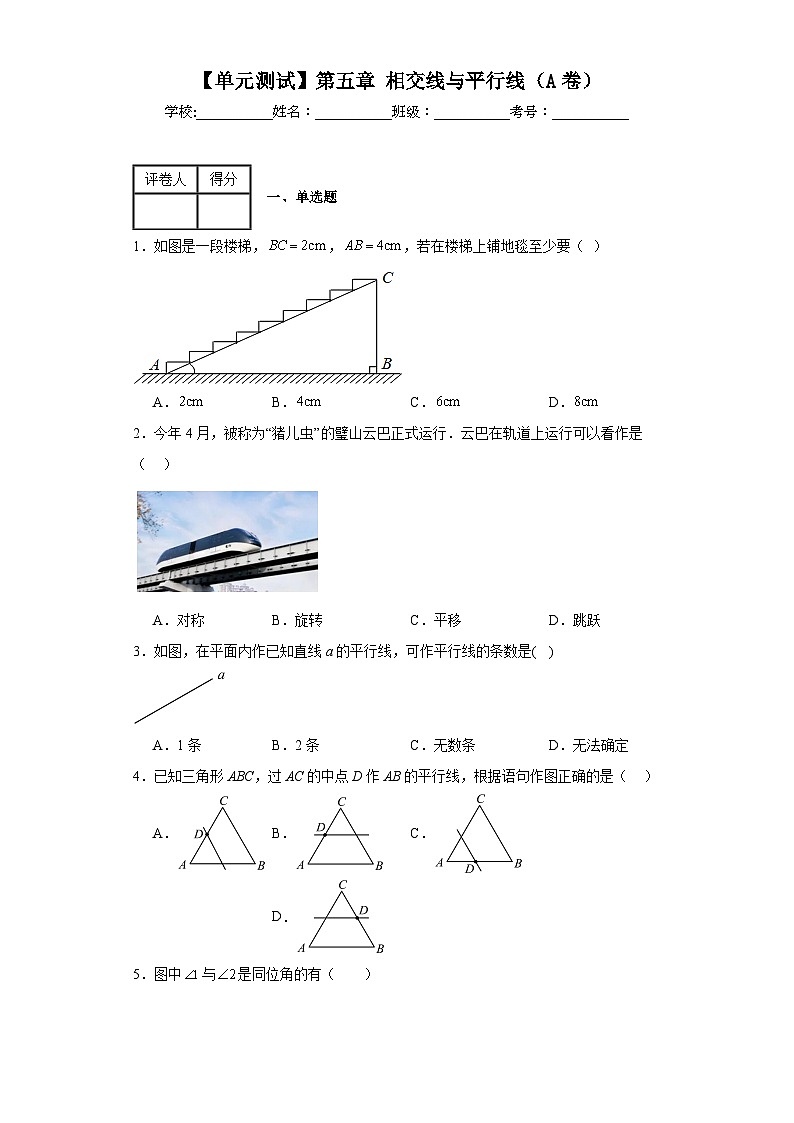
1.如图是一段楼梯,,,若在楼梯上铺地毯至少要( )
A. B. C. D.
2.今年4月,被称为“猪儿虫”的璧山云巴正式运行.云巴在轨道上运行可以看作是( )
A.对称 B.旋转 C.平移 D.跳跃
3.如图,在平面内作已知直线a的平行线,可作平行线的条数是( )
A.1条 B.2条 C.无数条 D.无法确定
4.已知三角形ABC,过AC的中点D作AB的平行线,根据语句作图正确的是( )
A. B. C. D.
5.图中与是同位角的有( )
A.1个 B.2个 C.3个 D.4个
6.春节过后,某村计划挖一条水渠将不远处的河水引到农田(记作点O),以便对农田的小麦进行灌溉,现设计了四条路段,,,,如图所示,其中最短的一条路线是( )
A.OA B.OB C.OC D.OD
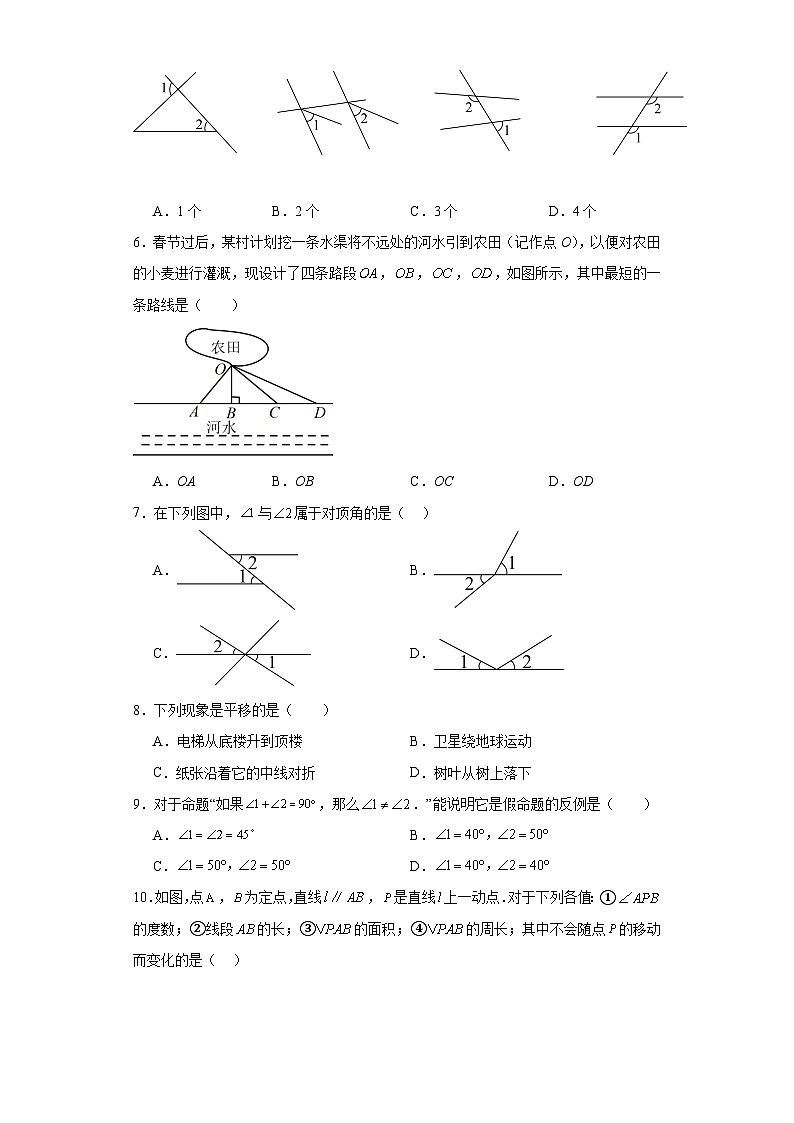
7.在下列图中,与属于对顶角的是( )
A. B.
C. D.
8.下列现象是平移的是( )
A.电梯从底楼升到顶楼 B.卫星绕地球运动
C.纸张沿着它的中线对折 D.树叶从树上落下
9.对于命题“如果,那么.”能说明它是假命题的反例是( )
A. B.
C. D.
10.如图,点,为定点,直线,是直线上一动点.对于下列各值:①的度数;②线段的长;③的面积;④的周长;其中不会随点的移动而变化的是( )
A.①③ B.①④ C.②③ D.①②
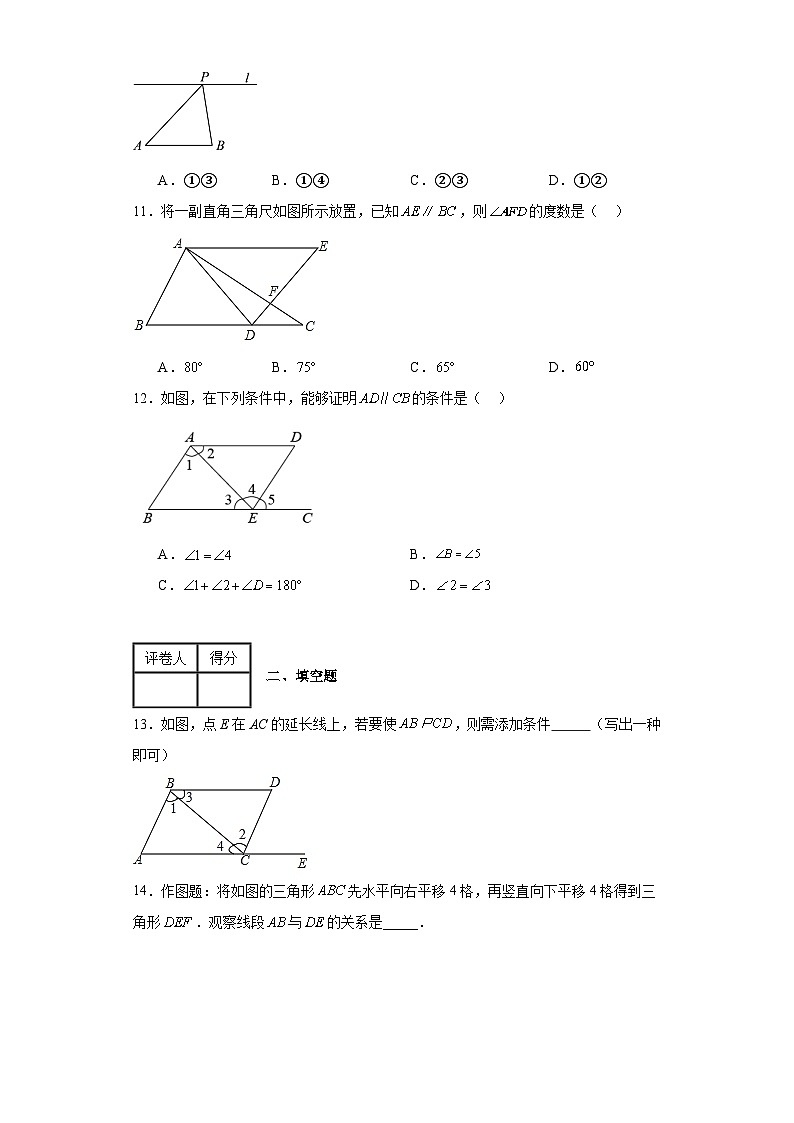
11.将一副直角三角尺如图所示放置,已知,则的度数是( )
A. B. C. D.
12.如图,在下列条件中,能够证明的条件是( )
A. B.
C. D.
| 二、填空题 |
13.如图,点E在AC的延长线上,若要使,则需添加条件 (写出一种即可)
14.作图题:将如图的三角形先水平向右平移4格,再竖直向下平移4格得到三角形.观察线段与的关系是_____.
15.如图,将长为5cm,宽为3cm的长方形ABCD先向右平移2cm,再向下平移1cm,得到长方形,则阴影部分的周长为 cm.
16.如图,已知直线,将一块三角板的直角顶点放在直线a上,如果,那么 度.
17.光线在不同介质中传播速度不同,从一种介质射向另一种介质时会发生折射.如图,水面与水杯下沿平行,光线从水中射向空气时发生折射,光线变成,点在射线上,已知,,则的度数为 .
18.下列说法:①对顶角相等;②两点之间的线段是两点间的距离;③过一点有且只有一条直线与已知直线平行;④过一点有且只有一条直线与已知直线垂直;⑤一个锐角的补角一定比它的余角大90°,正确的有 .(填序号)
19.如图:与成内错角的是 ;与成同旁内角的是 .
20.如图,过直线AB上一点O作射线,,平分,则的度数为 .
21.如图,将周长为厘米的沿射线方向平移厘米得到,那么四边形的周长为 厘米.
22.下列命题:①经过直线外一点,有且只有一条直线与这条直线平行;②在同一平面内,过一点有且只有一条直线与已知直线垂直;③直线外一点到这条直线的垂线段的长度,叫做点到直线的距离;④如果直线,,那么.其中是真命题的有 .(填序号)
23.如图,点E、F分别是梯形两腰的中点,联结、,如果图中的面积为1.5,那么梯形的面积等于 .
24.如图,为直线上一点,将一直角三角板的直角顶点放在点处,一边在射线上,另一边在直线的上方.将三角板绕点以每秒3°的速度沿逆时针方向旋转一周.则经过 秒后,.
| 三、解答题 |
25.已知直线经过点,,是的平分线.
(1)如图1,若,求;
(2)如图1,若,直接写出______;(用含的式子表示)
(3)将图1中的绕顶点顺时针旋转到图2的位置,其他条件不变,(2)中的结论是否还成立?试说明理由.
26.在正方形网格中,小正方形的顶点称为“格点”,每个小正方形的边长均为1,内角均为直角,的三个顶点均在“格点”处.
(1)将平移,使得点B移到点的位置,画出平移后的;
(2)利用正方形网格画出的高;
(3)连接、,利用全等三角形的知识证明.
27.如图,已知点O在直线AB上,射线OE平分∠AOC,过点O作OD⊥OE,G是射线OB上一点,连接DG,使∠ODG+∠DOG=90°.
(1)求证:∠AOE=∠ODG;
(2)若∠ODG=∠C,试判断CD与OE的位置关系,并说明理由.
28.如图1,,直线外有一点,连接,.
(1)证明:;
(2)如图2,延长至点,连接,平分,平分,且与交于点,求与的数量关系;
(3)如图3,在2的条件下,,,连接,且,,求的度数.
参考答案:
1.C
【分析】把楼梯的横竖向上向左平移,构成一个矩形,则AB+BC即为所求.
【详解】解:∵△ABC是直角三角形,BC=2cm,AB=4cm,
∴如果在楼梯上铺地毯,那么至少需要地毯为AB+BC=6米.
故选C.
【点睛】本题考查的是生活中的平移现象,解决此题的关键是要利用平移的知识.
2.C
【分析】根据平移与旋转定义判断即可.
【详解】解:云巴在轨道上运行可以看作是数学上的平移.
故选:C.
【点睛】本题考查对平移与旋转的理解及在实际当中的运用.平移是物体运动时,物体上任意两点间,从一点到另一点的方向与距离都不变的运动;旋转是物体运动时,每一个点离同一个点(可以在物体外)的距离不变的运动,称为绕这个点的转动,这个点称为物体的转动中心.所以,它并不一定是绕某个轴的.正确理解平移与旋转的定义是解题的关键.
3.C
【分析】根据平行线的定义和性质求解即可.
【详解】解:在同一平面内与已知直线平行的直线有无数条,
∴在平面内作已知直线a的平行线,可作平行线的条数是无数条,
故选C.
【点睛】本题主要考查了平行线的定义和性质,熟知相关知识是解题的关键.
4.B
【分析】根据中点的定义,平行线的定义判断即可.
【详解】解:过AC的中点D作AB的平行线,
正确的图形是选项B,
故选:B.
【点睛】本题考查作图——复杂作图,平行线的定义,中点的定义等知识,解题关键是理解题意,灵活运用所学知识解决问题.
5.B
【分析】根据同位角的定义作答.
【详解】解:第1个图和第4个图中的与是同位角,有2个,
故选:B.
【点睛】本题考查了同位角的识别,两条直线被第三条直线所截,在截线的同侧,在两条被截直线的同旁的两个角是同位角.如果两个角是同位角,那么它们一定有一条边在同一条直线上.
6.B
【分析】根据垂线段的性质:垂线段最短,可得答案.
【详解】由垂线段最短,得
四条线段,,,,如图所示,
其中最短的一条路线是,
故选:B.
【点睛】本题考查了垂线段的的性质,熟记性质是解题关键.
7.C
【分析】根据对顶角的定义:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角,可得结论.
【详解】解:在选项B、D中,与的两边都不互为反向延长线,A选项没有公共点,所以不是对顶角,是对顶角的只有选项C.
故选:C.
【点睛】本题主要考查了对顶角的定义,熟记有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角是解答此题的关键.
8.A
【分析】平移是物体运动时,物体上任意两点间,从一点到另一点的方向与距离都不变的运动,根据平移的定义分析即可.
【详解】解:A、电梯从底楼升到顶楼为平移现象,故该选项符合题意;
B、卫星绕地球运动为旋转现象,故该选项不符合题意;
C、纸张沿着它的中线对折是轴对称现象,故该选项不符合题意;
D、树叶从树上落下既不是旋转也不是平移,故该选项不符合题意.
故选:A.
【点睛】本题考查了平移现象,熟练根据平移的定义联系实际生活是解题的关键.
9.A
【分析】能说明是假命题的反例就是能满足已知条件,但不满足结论的例子,逐项判断即可.
【详解】A、满足,但不满足,满足题意;
B、满足命题“如果,那么”,不符合题意;
C、不满足命题“如果,那么”,不符合题意;
D、不满足命题“如果,那么”,不符合题意;
故选:A.
【点睛】考查了命题与定理的知识,理解能说明它是假命题的反例的含义是解决本题的关键
10.C
【分析】根据运动得出的大小不断发生变化;求出长为定值;由于P到的距离为定值,再根据三角形的面积公式进行计算即可;根据运动得出不断发生变化.
【详解】解:当P点移动时,发生变化,
∴①错误;
∵A、B为定点,
∴长为定值,
∴②正确;
∵点A,B为定点,直线,
∴P到的距离为定值,故的面积不变,
∴③正确;
当P点移动时,的长发生变化,
∴的周长发生变化,
∴④错误;
综上,正确的有②③,
故选:C.
【点睛】本题考查了平行线的性质,等底等高的三角形的面积相等,平行线间的距离的运用,熟记定理是解题的关键.
11.B
【分析】根据平行线的性质及三角形内角定理解答.
【详解】解:由三角板的性质可知.
∵,
∴,
∴.
∴.
故选:B.
【点睛】本题考查的是平行线的性质及三角形内角和定理,平行线的性质:两直线平行同位角相等,同旁内角互补.三角形内角和定理:三角形的内角和等于.
12.D
【分析】根据平行线的判定定理逐项分析判断即可求解.
【详解】解:A. ,内错角相等两直线平行,能判定;故A不符合题意;
B. ,同位角相等两直线平行,能判定;故B不符合题意;
C. ,同旁内角互补两直线平行,能判定;故C不符合题意;
D. ,内错角相等两直线平行,能判定,故D符合题意.
故选:D.
【点睛】本题考查了平行线的判定方法,掌握平行线的判定方法“同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行”是解题的关键.
13.∠1=∠2 等 (写出一种即可)
【分析】根据平行线的判定定理得出直接得出即可.
【详解】解:∵当∠1 =∠2时,(内错角相等,两直线平行);
∴若要使,则需添加条件∠1 =∠2;
故答案为:∠1=∠2.
【点睛】本题主要考查了平行线的判定,熟练掌握平行线的判定定理是解题关键.
14.AB∥DE,AB=DE
【分析】根据网格结构找出平移后的点D、E、F的位置,然后解答即可.
【详解】解:△DEF如图所示,
AB∥DE,AB=DE.
故答案为:AB∥DE,AB=DE.
【点睛】本题考查了平移的性质,熟练掌握网格结构准确找出对应点的位置是解题的关键.
15.32
【分析】阴影部分的周长刚好是长方形周长的两倍,据此作答即可.
【详解】∵长方形的长为5cm,宽为3cm,
∴长方形的周长为:5+3+3+5=16(cm),
根据图形可知:阴影部分的周长为:,
即:阴影部分的周长刚好是长方形周长的两倍,
即阴影部分的周长为:16×2=32(cm),
故答案为:32.
【点睛】本题考查了图形的平移的知识,根据图形的平移判断出阴影部分的周长刚好是长方形周长的两倍,是解答本题的关键.
16.
【分析】根据平行线得到内错角相等,在根据直角即可得到答案.
【详解】解:∵,
∴,
∵,,
∴
故答案为.
【点睛】本题考查平行线性质:两直线平行内错角相等.
17./25度
【分析】根据平行线的性质求得,根据即可求解.
【详解】解:∵,
∴.
∵,
∴;
故答案为25°.
【点睛】本题考查了平行线的性质与判定,掌握平行线的性质与判定是解题的关键.
18.①⑤
【分析】根据对顶角、线段、直线、垂直的定义、平行线的性质及余补角的性质可直接进行求解.
【详解】解:①对顶角相等,原说法正确;②两点之间的线段长度是两点间的距离,原说法错误;③过直线外一点有且只有一条直线与已知直线平行,原说法错误;④在同一平面内,过一点有且只有一条直线与已知直线垂直,原说法错误;⑤一个锐角的补角一定比它的余角大90°,原说法正确;
综上所述:正确的有①⑤;
故答案为①⑤.
【点睛】本题主要考查对顶角、线段、直线、垂直的定义、平行线的性质及余补角的性质,熟练掌握相关概念及性质是解题的关键.
19. 、和 、、和
【分析】准确识别内错角、同旁内角的关键,是弄清哪两条直线被哪一条线所截.也就是说,在辨别这些角之前,要弄清哪一条直线是截线,哪两条直线是被截线.
【详解】解:如图,与成内错角的是、和,与成同旁内角的是:、、和.
故答案分别是:、和,、、和.
【点睛】本题考查了同位角、内错角、同旁内角.在复杂的图形中识别同位角、内错角、同旁内角时,应当沿着角的边将图形补全,或者把多余的线暂时略去,找到三线八角的基本图形,进而确定这两个角的位置关系.
20./75度
【分析】先根据,求出,再根据平分,即可得出答案.
【详解】解:∵,
∴,
∵平分,
∴.
故答案为:.
【点睛】本题主要考查了角平分线的有关计算,领补角的计算,解题的关键是根据邻补角求出.
21.
【分析】利用平移的性质得到,然后根据可计算出四边形的周长.
【详解】解:沿射线方向平移厘米得到,
,
,
cm.
即四边形的周长为.
故答案为.
【点睛】本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行或共线且相等.
22.①②③
【分析】根据平行公理及其推论、垂线的性质、点到直线的距离定义等分析判断即可.
【详解】解:①经过直线外一点,有且只有一条直线与这条直线平行,正确,为真命题;
②在同一平面内,过一点有且只有一条直线与已知直线垂直,正确,为真命题;
③直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,正确,为真命题;
④如果直线,,那么,原命题为假命题.
综上所述,真命题有①②③.
故答案为:①②③.
【点睛】本题主要考查了命题与定理的知识,解题关键是理解平行公理及其推论、垂线的性质、点到直线的距离定义等知识.
23.6
【分析】过点A作于H,交于G,根据梯形中位线定理得到,根据三角形的面积公式、梯形的面积公式计算,得到答案.
【详解】解:过点A作于H,交于G,如图,
∵点E、F分别是梯形两腰的中点,
∴是梯形的中位线,
∴,
∴,,
∵,
∴,
∴,
∴,
故答案为:6.
【点睛】本题考查的是梯形的中位线、三角形的面积计算,掌握梯形中位线定理是解题的关键.
24.10或70/70或10
【分析】分两种情况讨论,利用旋转的性质即可求解.
【详解】解:如图,,
∵,,
∴,,
∵将三角板绕点以每秒3°的速度沿逆时针方向旋转,
∴(秒);
如图,,
∵,,
∴,,
∵将三角板绕点以每秒3°的速度沿逆时针方向旋转,
∴旋转角为,
∴(秒);
故答案为:10或70.
【点睛】本题考查了垂直的定义、角的和差等知识,解题的关键是理解题意,画出图形,利用垂直的定义求解即可.
25.(1)
(2)
(3)成立,
【分析】(1)如图1,根据平角的定义和,从而,结合求得,由角平分线定义得,利用角的差可得结论;
(2)如图1,根据平角的定义和,从而,结合求得,由角平分线定义得,利用角的差可得结论;
(3)如图2,根据平角的定义得,根据角的差可得(2)中的结论还成立.
【详解】(1)解:∵,
∴,
∵,
∴,,
∵平分,
∴,
∴;
(2)解:∵,
∴,
∵,
∴,
∴,
∵平分,
∴,
∴;
(3)解:(2)中的结论还成立.
理由如下:
∵,,
∴
∵平分
∴
∵
∴.
【点睛】本题考查了角平分线的定义、平角的定义及角的和与差,能根据图形确定所求角和已知各角的关系是解此题的关键.
26.(1)见解析
(2)见解析
(3)见解析
【分析】(1)利用平移变换的性质分别作出A,B,C的对应点,,即可;
(2)根据三角形的高的定义画出图形即可;
(3)证明,可得结论.
【详解】(1)过点作,且,再沿着向右移动两个单位,再向上移动五个单位,就可得到点,连接,,即可得到
(2)设从点的位置向右两个单位的点为,连接,则就是所求的高
(3)设交于点J.
在和中,
,,,
∴,
∴,
∵,
∴,
∴,
∴.
【点睛】本题考查作图平移变换,全等三角形的判定和性质等知识,解题的关键是掌握平移变换的性质,正确寻找全等三角形解决问题.
27.(1)证明见解析
(2)CDOE,理由见解析
【分析】(1)由OD⊥OE得到∠EOC+∠COD=∠AOE+∠DOG=90°,再利用等角的余角相等即可证明∠AOE=∠ODG;
(2)证明∠EOC=∠C,利用内错角相等两直线平行,即可证明CDOE.
【详解】(1)证明:∵OD⊥OE,
∴∠EOC+∠COD=∠AOE+∠DOG=90°,
∵∠ODG+∠DOG=90°,
∴∠AOE=∠ODG;
(2)解:CDOE.理由如下:
由(1)得∠AOE=∠ODG,
∵射线OE平分∠AOC,
∴∠AOE=∠EOC,
∵∠ODG=∠C,
∴∠EOC=∠C,
∴CDOE.
【点睛】本题考查了角平分线定义,垂直的定义,平行线的判定,等角的余角相等,正确识图是解题的关键.
28.(1)证明见解析
(2)
(3)
【分析】(1)过点作,根据平行线性质即可得到角度关系,即可求证;
(2)过点作,过点作根据平行线性质得到角度关系即可得到答案;
(3)过点做,过点作,根据平行线性质得到角度关系即可得到答案.
【详解】(1)证明:过点作,
∵,,
∴
∴,,,
∴,
∴;
(2)解:∵平分,设,
又∵平分,设,
∴,,
过点作,
∵,
∴,
∴,,
∴,,
∴,
过点作,
∴,
∴,,
∴
∴;
(3)设,
过点做,
∵,,
∴,,
∴,
∵,
∴,
过点作,
∴,
∴,,
∴,
∴,
∵,,
∴,
∵,
∴,
∴,
∵,,
∴,
由(2)知,
∴,
∵,
∴,
∴,
∴,
∴,
∴.
【点睛】本题考查根据平行线的性质,解题的关键是作平行辅助线转换角度关系.









