数学七年级下册7.5 多边形的内角和与外角和课文配套ppt课件

这是一份数学七年级下册7.5 多边形的内角和与外角和课文配套ppt课件，共34页。PPT课件主要包含了学习目标，情景引入，新知探究，对顶角，操作与探究，你有什么发现，你能说明理由吗，过C点作CE∥AB，∵CE∥AB，新知巩固等内容，欢迎下载使用。
1.掌握多边形外角的概念，并能识别多边形的外角．
2.通过由特殊到一般的探索，理解并掌握“多边形外角和等于360°”，并能运用这一性质进行计算．
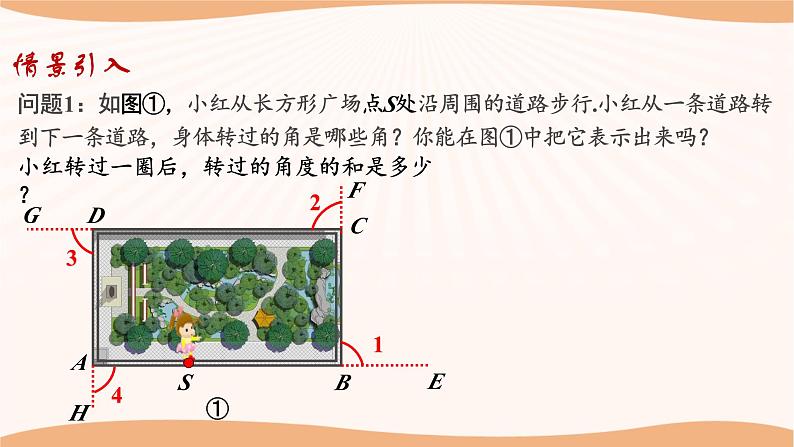
问题1：如图①，小红从长方形广场点S处沿周围的道路步行.小红从一条道路转到下一条道路，身体转过的角是哪些角？你能在图①中把它表示出来吗？
小红转过一圈后，转过的角度的和是多少？
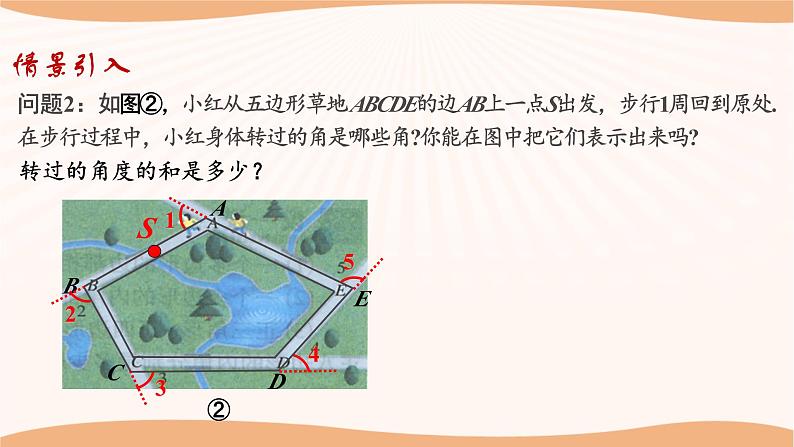
问题2：如图②，小红从五边形草地 ABCDE的边AB上一点S出发，步行1周回到原处.在步行过程中，小红身体转过的角是哪些角?你能在图中把它们表示出来吗?
转过的角度的和是多少？
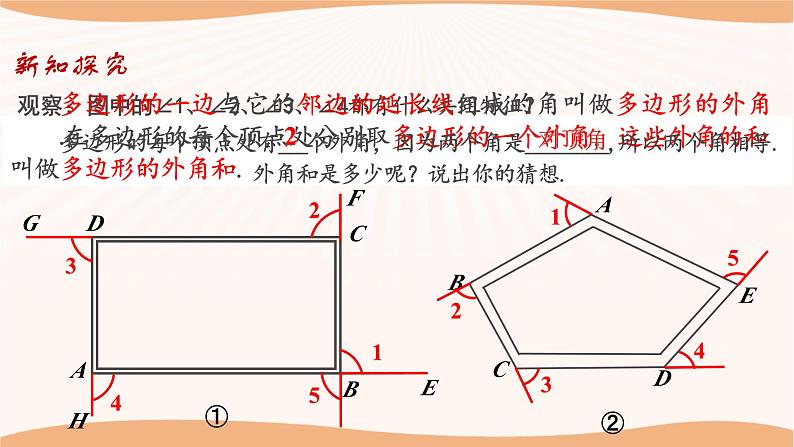
在多边形的每个顶点处分别取多边形的一个外角，这些外角的和叫做多边形的外角和.
多边形的每个顶点处有___个外角，因为两个角是________,所以两个角相等.
观察：图中的∠1、∠2、∠3、∠4都有什么共同特征？
多边形的一边与它的邻边的延长线组成的角叫做多边形的外角.
外角和是多少呢？说出你的猜想.
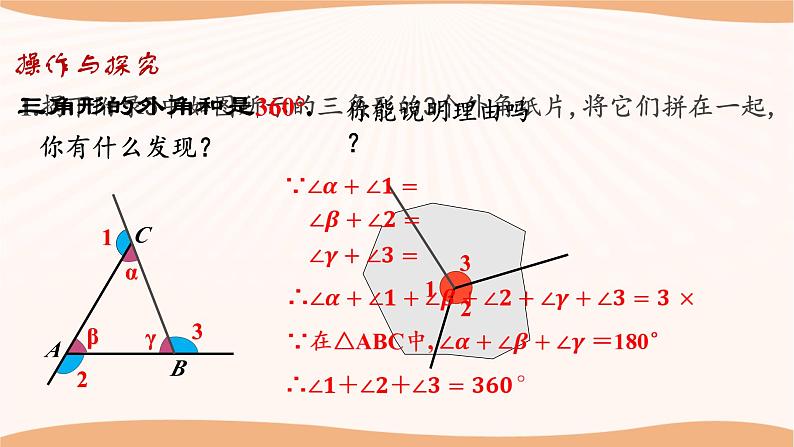
1.揭下附录5中如图所示的三角形的3个外角纸片,将它们拼在一起,
三角形的外角和是360°.
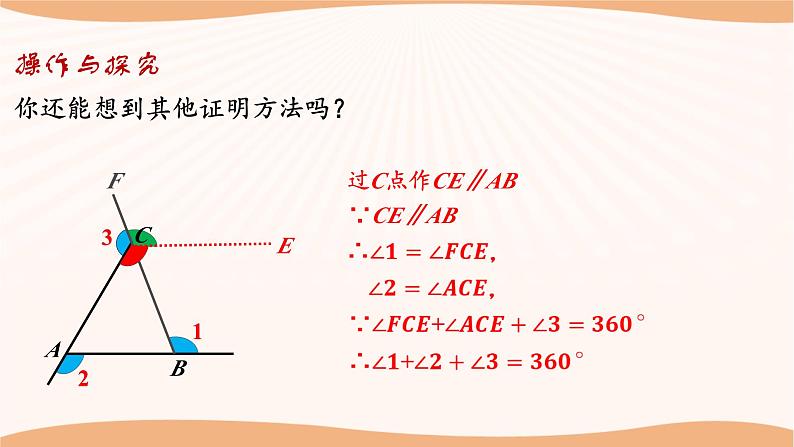
你还能想到其他证明方法吗？
2.揭下附录5中的四边形、五边形的外角纸片,分别将它们拼在一起,你有什么发现？
四边形、五边形的外角和都是360°.
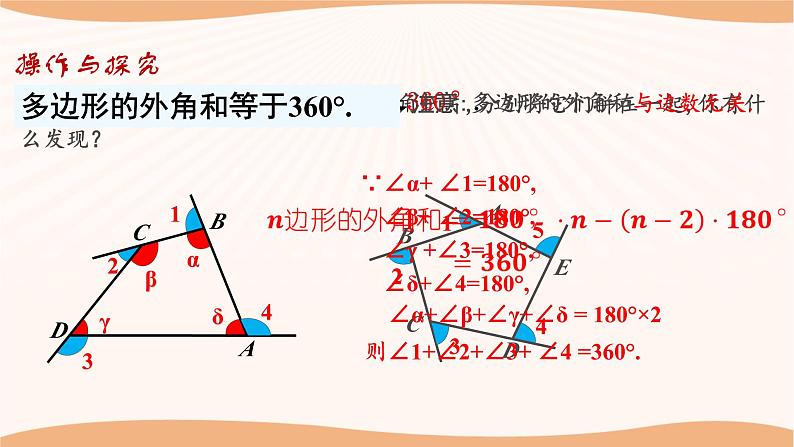
∵∠α+ ∠1=180°, ∠β+ ∠2=180°, ∠γ +∠3=180°, ∠δ+∠4=180°,
∠α+∠β+∠γ+∠δ = 180°×2
则∠1+∠2+∠3+ ∠4 =360°.
多边形的外角和等于360°.
注意:多边形的外角和与边数无关.
小红转过一圈后，转过的角度的和是360°
1.如图，∠ADC是________的外角，∠AOC是______________的外角，△AEC的外角是________．
2.七边形的外角和为______；
3.若一个多边形的每个外角都是72°，这是_____边形；
解：设这个多边形的边数为n.
4. 已知四边形的四个外角(每个顶点处分别取一个)的度数比为 1∶2∶3∶4，求该四边形各外角的度数．
解：设四边形的最小外角为x°，则其他三个外角分别为2x°，3x°，4x°， x°＋2x°＋3x°＋4x°＝360°，解得x＝36， 2x＝72，3x＝108，4x＝144， 该四边形各外角的度数分别为36°，72°，108°，144°.
例1.一个多边形的每一个内角都比与其相邻的外角大36°， 求这个多边形的边数；
解：设一个外角为x°，则与其相邻的内角为(x＋36)°. ∵多边形的外角和与其相邻的内角互补， ∴x＋x＋36＝180，解得x＝72， 360°÷72°＝5， 即这个多边形的边数为5.
例2.从图中的五边形ABCDE纸片中剪去一个三角形，剩余部分是几边形？ 它们的内角和、外角和分别是多少？
四边形，内角和360°，外角和360°
五边形，内角和540°，外角和360°
六边形，内角和720°，外角和360°
其它多边形呢?你能发现其中的规律吗？
1.一个多边形的内角和比它的外角和的3倍少180°,求这个多边 形的边数．
解：设这个多边形的边数是n，由题意得(n－2)×180°＝3×360°－180°，解得n＝7，∴这个多边形的边数是7.
3.如图，小明从点A出发沿直线前进10 m到达点B，向左转30°后，又沿直线前进10 m到达点C ，再向左转30°，…，照这样走下去，他第一次回到出发地点A时，走的路程一共是______.
360°÷30°=12
4.如图，在△ABC中，∠A=27°，∠B=48°，∠ACD是△ABC的一个外角，则∠ACD等于______.
请你思考∠ACD与△ABC的内角有何联系吗？
三角形的一个外角等于与它不相邻的两个内角的和.
5.如图，求∠A＋∠B＋∠C＋∠D＋∠E＋∠F的度数.
变式：如图，求∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＋∠H的度数.
（2）剩下的多边形为四边形,此时多边形内角和为_____,外角和不变,仍为_____;
（1）剩下的多边形为五边形,此时多边形内角和为_____,外角和不变,仍为_____;
（3）剩下的多边形为三角形,此时多边形内角和为_____,外角和不变,仍为_____.
6.把一个四边形剪去一个角,将得到几边形?此时,多边形的内角和与外角和有什么变化?
剪去一个角后，剩下的多边形分3种情况:
1.判断：(1)五边形的外角和大于四边形的外角和；(　　) (2)三角形的外角和为180°.(　　)
3.内角和与外角和相等的图形是_________.
2.若某多边形的边数增加1，则这个多边形的外角和_______.
4.一个多边形的内角和与外角和之和为2 520°，则这个多边形的边数为____．
5.一个机器人从点O出发，每前进1米，就向右转体a°（1＜a＜180º），照这样走下去，如果他恰好能回到O点，且所走过的路程最短，则a的值等于 ______．
6.如果一个多边形的内角和等于其外角和的2倍，求这个多边形的边数．
7.已知一个多边形有两个内角是直角，其余的内角都等于150°，求这个多边形的边数．
解：设这个多边形的边数为n.由题意，得90°×2＋(n－2)×150°＝(n－2)×180°，解得n＝8.答：这个多边形的边数是8.
解：设这个多边形是n边形．根据题意，得(n－2)·180°＝2×360°，解得n＝6.故这个多边形的边数是6.
8.已知一个多边形的每一个内角都相等，且每一个内角与相邻外角的差都是90°，求这个多边形的内角和及对角线的条数.