【期中真题】湖北省武汉市部分学校2022-2023学年高一上学期期中联考数学试题.zip

2022~2023学年度第一学期

武汉市部分学校高中一年级期中调研考试

数学试卷

本试卷共5页，22小题，全卷满分150分．考试用时120分钟．

注意事项：

1．答题前，先将自己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码贴在答题卡上的指定位置．

2．选择题的作答：每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑．写在试卷、草稿纸和答题卡上的非答题区域均无效．

3．非选择题的作答：用黑色签字笔直接答在答题卡上对应的答题区域内．写在试卷、草稿纸和答题卡上的非答题区域均无效．

4．考试结束后，请将本试卷和答题卡一并上交．

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. 已知集合，或，则（    ）

A. 或 B.

C.  D. 或

2. 下列图象中，以为定义域，为值域的函数是（    ）

A.  B.

C.  D.

3. 一家商店使用一架两臂不等长的天平称黄金.一位顾客到店里购买10黄金，售货员先将5的砝码放在天平左盘中，取出一些黄金放在天平右盘中使天平平衡；再将5的砝码放在天平右盘中，再取出一些黄金放在天平左盘中使天平平衡；最后将两次称得的黄金交给顾客.若顾客实际购得的黄金为，则（    ）

A.  B.  C.  D. 以上都有可能

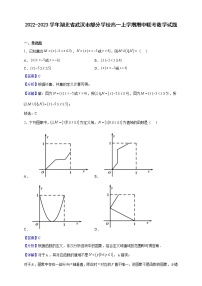
4. 某地区居民生活用电分高峰和低谷两个时段进行分时计价．

若某家庭7月份的高峰时间段用电量为250千瓦时，低谷时间段用电量为150千瓦时，则该家庭本月应付电费（    ）

A. 190.7元 B. 197.7元 C. 200.7元 D. 207.7元

5. 已知命题“，使”是真命题，则实数的取值范围是（    ）

A. 或 B.

C. 或 D.

6. 关于的不等式的解集为，则关于的不等式的解集为（    ）

A.  B.

C. 或 D. 或

7. 已知偶函数的定义域为，且对于任意均有成立，若，则实数的取值范围是（    ）

A.  B.

C.  D.

8. 若关于的不等式有且只有一个整数解，则实数的取值范围是（    ）

A. 或 B.

C. 或 D.

二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．

9. 设集合，，，则下列关系中正确的是（    ）．

A.  B.  C.  D.

10. 已知集合，则实数取值为（    ）

A.  B.  C.  D.

11. 设a，b为两个正数，定义a，b算术平均数为，几何平均数为．上个世纪五十年代，美国数学家D.H. Lehmer提出了“Lehmer均值”，即，其中p为有理数．下列结论正确的是（    ）

A.  B.

C.  D.

12. 已知函数是定义在上的奇函数，当时，，则下列结论正确的有（    ）

A.  B. 的单调递增区间为

C. 当时， D. 的解集为

三、填空题：本题共4小题，每小题5分，共20分．

13. 已知，若，则实数=___________.

14. 已知集合的子集只有两个，则实数的值为______．

15. 若函数是奇函数，，则__________ .

16. 若实数，，且，则的最小值为______．

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

17. 已知命题，命题．

（1）若，则是的什么条件？

（2）若是的必要不充分条件，求实数的取值范围．

18. 已知关于的不等式的解集为（其中）．

（1）求实数a，b的值；

（2）解不等式．

19 已知函数．

（1）试判断函数在区间上的单调性，并用函数单调性定义证明；

（2）若，使成立，求实数的范围．

20. 2020年初新冠肺炎袭击全球，严重影响人民生产生活．为应对疫情，某厂家拟加大生产力度．已知该厂家生产某种产品的年固定成本为200万元，每生产千件，需另投入成本．当年产量不足50千件时，（万元）；年产量不小于50千件时，（万元）．每千件商品售价为50万元．通过市场分析，该厂生产的商品能全部售完．

（1）写出年利润（万元）关于年产量（千件）的函数解析式；

（2）当年产量为多少千件时，该厂在这一商品的生产中所获利润最大？最大利润是多少？

21. 已知二次函数的最小值为1，且满足，，点在幂函数的图象上．

（1）求和的解析式；

（2）定义函数试画出函数的图象，并求函数的定义域、值域和单调区间．

22 已知函数，．

（1）解关于的不等式；

（2）若实数使得关于的方程对任意恒有四个不同的实根，求的取值范围．