初中数学鲁教版 (五四制)九年级上册6 二次函数的应用学案及答案

课题

6　二次函数的应用

课时

第1课时

上课时间

教学目标

1.经历探究几何图形中的最值问题,学会用二次函数来解决几何图形中最值问题.体会二次函数的应用意义以及数学的转化思想.

2.通过自主探究,理解二次函数的应用.经过合作交流,了解二次函数解决几何图形最值问题的基本思路,提高学生的分析总结能力.

3.通过几何图形中的最值问题的探究活动,建立学生对二次函数应用的以及数形结合的思维,培养学生勇于探索的学习习惯.

教学

重难点

重点:利用二次函数解决图形问题.

难点:能根据问题灵活解设二次函数,选用合适的方法确定二次函数表达式.

教学活动设计

二次设计

课堂导入

1.二次函数y=ax2+bx+c,b2=ac,且x=0时y=-4,则(　　)

(A)y最大=-4 (B)y最小=-4           (C)y最大=-3 (D)y最小=3

2.根据已知条件确定二次函数的表达式.

(1)图象的顶点为(2,3),且经过点(3,6);

(2)图象经过点(1,0),(3,0)和(0,9);

(3)图象经过点(1,0),(0,-3),且对称轴是直线x=2.

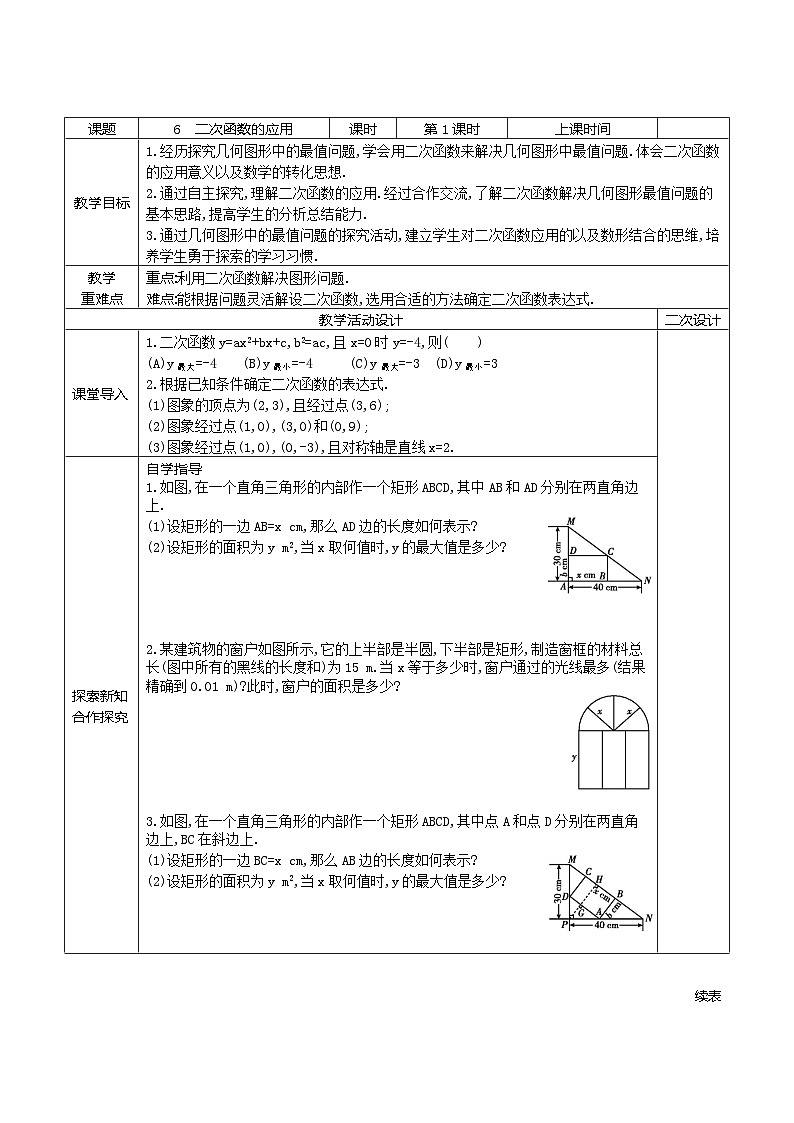
探索新知

合作探究

自学指导

1.如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.

(1)设矩形的一边AB=x cm,那么AD边的长度如何表示?

(2)设矩形的面积为y m2,当x取何值时,y的最大值是多少?

2.某建筑物的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长(图中所有的黑线的长度和)为15 m.当x等于多少时,窗户通过的光线最多(结果精确到0.01 m)?此时,窗户的面积是多少?

3.如图,在一个直角三角形的内部作一个矩形ABCD,其中点A和点D分别在两直角边上,BC在斜边上.

(1)设矩形的一边BC=x cm,那么AB边的长度如何表示?

(2)设矩形的面积为y m2,当x取何值时,y的最大值是多少?

探索新知

合作探究

4.思考

你能总结出解决此类问题“最大面积”的基本思路吗?

5.自学课本96~97页,利用二次函数解决几何图形的例题.

学生看书,教师巡视,老师督促每一位学生认真,紧张地自学,鼓励学生质疑问难.

合作探究

1.讨论

小组讨论自学指导中出现疑问的地方.

2.组织学生探究利用二次函数解决几何图形的基本思路.

3.根据问题选择设立合适的二次函数表达式,简便解题.

教师指导

1.易错点:

(1)注意二次函数的表达式设立后的符号问题,坐标点代入易错.

(2)理清题目中的变量跟常量,选择设立合适的二次函数表达式解题.

2.归纳小结:

解决此类“最大面积”问题的基本思路:

第一步:审题理解问题;

第二步:分析问题中的变量和常量,设自变量;

第三步:分析问题中的变量和常量之间的关系,建立函数的表达式;

第四步:确定自变量的取值范围;

第五步:根据顶点坐标公式或配方法求出最大值或最小值(在自变量的取值范围内).

3.方法规律:

(1)理清题目中的变量和常量.

(2)熟记常用几何图形的面积公式.

(3)选择合适的二次函数表达式解题.

当堂训练

1.有一抛物线形的立交桥,这个桥拱的最大高度为 16 m,跨度为40 m.现把它的图形放在平面直角坐标系中,如图所示,则该抛物线的表达式为　. 

2.已知抛物线y=-x2+1的顶点为P,点A是第一象限内该二次函数图象上一点,过点A作x轴的平行线交二次函数图象于点B,分别过点B,A作x轴的垂线,垂足分别为C,D,连接PA,PD,PD交于点E,△PAD与△PEA相似吗?试说明理由.

板书设计

用二次函数解决面积最值问题

1.利用二次函数解决图形最值问题

           2.利用二次函数解决图形问题的基本思路

3.选用合适的二次函数表达式解题

教学反思

我从函数思想方面来反思我们的教学行为,函数到底是解决现实中的什么问题,它依托怎么样的工具.搞清楚数与形的结合方式,是先形,还是先数.找到函数的基本模型和具体的数与形的转化过程.教学中不能忽视坐标系的作用,在重视具体函数研究的同时,加强小组合作研讨.