2022北京首都师大附中初一12月月考数学（教师版）

2022北京首都师大附中初一12月月考

数    学

一、选择题（本题共12小题，共24分）

1.     下列几何体中，是圆柱的为(    )

A.  B.

C.  D.

2.     原子钟是以原子的规则振动为基础的各种守时装置的统称，其中氢脉泽钟的精度达到了年误差不超过秒数据用科学记数法表示为(    )

A.  B.  C.  D.

3.     下列各式中运算正确的是(    )

A.  B.  C.  D.

4.     下列关于多项式的说法中，正确的是(    )

A. 它是三次三项式 B. 它是四次两项式

C. 它的最高次项是 D. 它的常数项是

5.     已知，则下列等式不一定成立的是(    )

A.  B.

C.  D.

6.     如图，点、在线段上，若，则(    )

A.  B.  C.  D.

7.     规定符号表示，两个数中较小的一个，规定符号表示两个数中较大的一个，例如，，则，的结果为(    )

A.  B.  C.  D.

8.     如图，点在直线上，若，则的大小为(    )

A.  B.  C.  D.

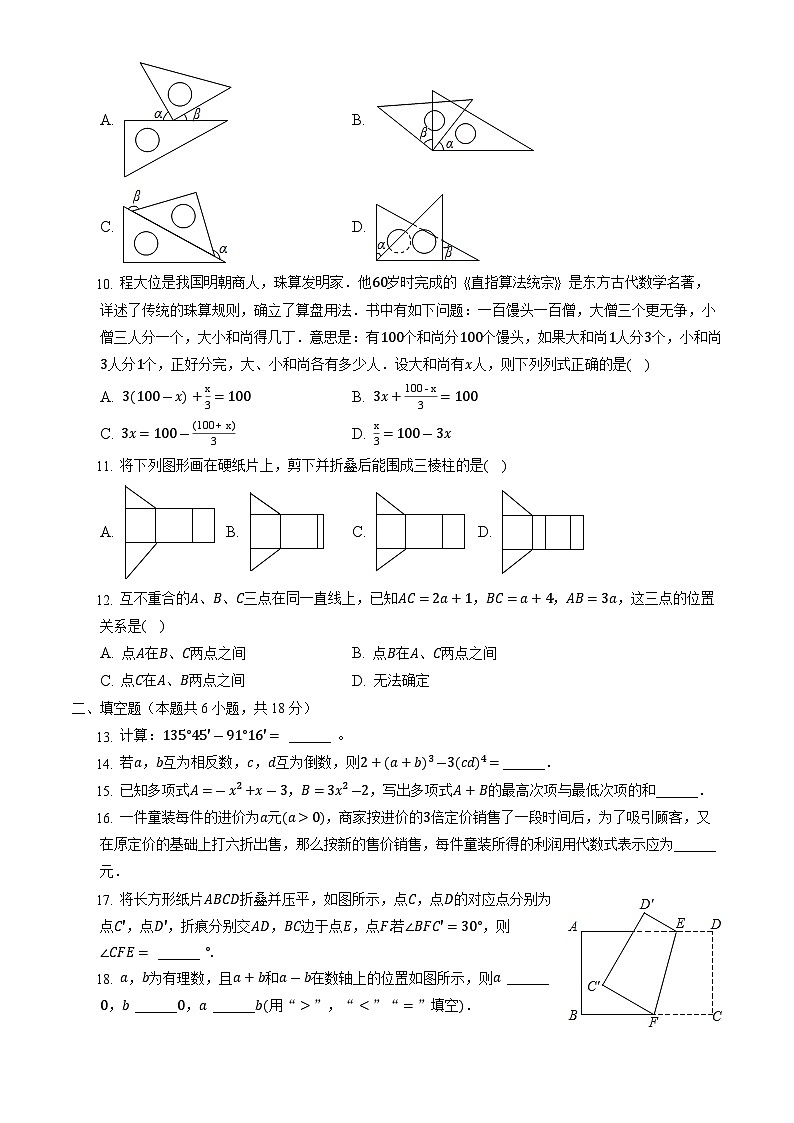
9.     将一副直角三角尺按如图所示的不同方式摆放，则图中锐角与相等的是(    )

A.  B.

C.  D.

10. 程大位是我国明朝商人，珠算发明家．他岁时完成的直指算法统宗是东方古代数学名著，详述了传统的珠算规则，确立了算盘用法．书中有如下问题：一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚得几丁．意思是：有个和尚分个馒头，如果大和尚人分个，小和尚人分个，正好分完，大、小和尚各有多少人．设大和尚有人，则下列列式正确的是(    )

A.  B.

C.  D.

11. 将下列图形画在硬纸片上，剪下并折叠后能围成三棱柱的是(    )

A.  B.  C.  D.

12. 互不重合的、、三点在同一直线上，已知，，，这三点的位置关系是(    )

A. 点在、两点之间 B. 点在、两点之间

C. 点在、两点之间 D. 无法确定

二、填空题（本题共6小题，共18分）

13. 计算： ______ 。
14. 若，互为相反数，，互为倒数，则______．
15. 已知多项式，，写出多项式的最高次项与最低次项的和______．
16. 一件童装每件的进价为元，商家按进价的倍定价销售了一段时间后，为了吸引顾客，又在原定价的基础上打六折出售，那么按新的售价销售，每件童装所得的利润用代数式表示应为______元．
17. 将长方形纸片折叠并压平，如图所示，点，点的对应点分别为点，点，折痕分别交，边于点，点若，则 ______
18. ，为有理数，且和在数轴上的位置如图所示，则 ______， ______， ______用“”，“”“”填空．

三、解答题（本题共9小题，共58分）

19. 解方程
20. ；
21. ．
22. 先化简，再求值．，其中，．
23. 如图，点在的边上，选择合适的画图工具按要求画图．
24. 反向延长射线，得到射线，画的角平分线；
25. 在射线上取一点，使得；
26. 在射线上作一点，使得最小；
27. 写出你完成的作图依据：______．
29. 如图所示，点在线段上，，点是线段的中点．
30. 若，则线段的长为______；
31. 在的条件下，点在直线上，若，则线段的长为______．

32. 已知关于的方程．
33. 若方程与关于的方程有相同的解，求的值；
34. 若方程的解是正整数，直接写出正整数的值是______．
35. 如图，已知，，平分，求的度数．
37. 已知，当时，的值为．
38. 当时，求的值．
39. 当时，的值为，求的值．
40. 设，当时，比较与的大小．
41. 如图，，射线在平面内．
42. 若与互补，则 ______；
43. 射线绕点从射线的反向延长线的位置出发，逆时针旋转角，平分．
44. 若，则的度数为______；
45. 是否存在的值，使得与互余，若存在，求出；若不存在，请说明理由．
47. 已知数轴上两点、，其中表示的数为，表示的数为对于在数轴一点不与点、点重合，若线段与的长度之比为，则称叫做点、的“倍伴随点”，记作．
48. 例如，图所示：若点是线段的中点时，有，则称点为点、的“倍伴随点”，记作．
50. 请根据上述规定回答下列问题：
51. 已知，如图，点，，为数轴上三个点，点表示的数是．
52. ______；
53. 比较、与的大小______用“”连接；
54. 已知点是数轴上点、的“倍伴随点”，请你直接写出点表示的数为______；
55. 已知数轴上三点，，，点、分别为、的中点，满足，且此时点是点、的“倍伴随点”，求的值及点表示的数．
    

参考答案

1.【答案】 

【解析】解：根据立体图形的定义及圆柱特征；

故选：．

根据立体图形的定义及其命名规则逐一判断即可。

本题主要考查立体图形，解题的关键是认识常见的立体图形

2.【答案】 

【解析】

【分析】

此题考查科学记数法的表示方法，表示时关键要正确确定的值以及的值．

科学记数法的表示形式为的形式，其中，为整数．确定的值时，要看把原数变成时，小数点移动了多少位，的绝对值与小数点移动的位数相同．当原数绝对值时，是正整数；当原数绝对值时，是负整数．

【解答】

解：，

故选B．  

3.【答案】 

【解析】解：、，所以选项错误；

B、与不能合并，所以选项错误；

C、，所以选项错误；

D、，所以选项正确．

故选：．

根据合并同类项得到，，，于是可对、、进行判断；由于与不是同类项，不能合并，则可对进行判断．

本题考查了合并同类项：把同类项的系数相加减，字母和字母的指数不变．

4.【答案】 

【解析】

【分析】

本题考查了多项式，解题的关键是掌握多项式的有关概念，并注意符号的处理几个单项式的和叫做多项式，每个单项式叫做多项式的项，其中不含字母的项叫做常数项．多项式中次数最高的项的次数叫做多项式的次数多项式的组成元素是单项式，即多项式的每一项都是一个单项式，单项式的个数就是多项式的项数，如果一个多项式含有个单项式，次数是，那么这个多项式就叫次项式，据此作答即可．

【解答】

解：多项式的次数是，有项，是四次三项式，故A、B错误；

它的最高次项是，故C正确；

它常数项是，故D错误．

故选C．  

5.【答案】 

【解析】解：、，等式一定成立，不符合题意；

B、，等式一定成立，不符合题意；

C、当时，等式不成立，不一定成立，符合题意；

D、，等式一定成立，不符合题意；

故选：．

A、根据等式的性质：等式两边同加减同一个数，等式仍然成立；

B、等式的两边同乘同一个数，等式仍然成立；

C、等式的两边同除同一个不为的数，等式仍然成立，逐一进行判断即可．

D、根据等式的性质：等式两边同加减同一个数，等式仍然成立；

本题考查了等式的性质，掌握等式的性质是关键．

6.【答案】 

【解析】解：由两边都加，得

，即，故B正确；

故选：．

根据等式的性质：两边都加，可得答案．

本题考查了两点间的距离，利用了等式的性质：等式的两边都加或减同一个数或同一个整式，结果不变．

7.【答案】 

【解析】解：符号表示，两个数中较小的一个，规定符号表示两个数中较大的一个，

，，

，．

故选：．

根据题意列出代数式进行计算即可．

本题考查的是有理数的大小比较，根据题意得出和的值是解题的关键．

8.【答案】 

【解析】解：．

，

，

，

又，

，

故选：．

根据垂直的定义可得，进而求出，再根据平角的定义求出答案．

本题考查垂线，角的计算，理解垂直的定义以及角的和差关系是正确解答的前提．

9.【答案】 

【解析】解：、与互余，不一定相等；

B、；

C、，但与都是钝角；

D、，，

；

故选：．

根据余角和补角的概念解答．

本题考查的是余角和补角，掌握余角和补角的概念是解题的关键．

10.【答案】 

【解析】解：设大和尚有人，则小和尚有人，

由题意得：；

故选：．

设大和尚有人，根据有个和尚分个馒头，如果大和尚人分个，小和尚人分个，正好分完，列出方程即可．

本题考查一元一次方程的应用，根据题意正确的列出方程，是解题的关键．

11.【答案】 

【解析】解：根据三棱柱的展开图特点可得答案可以围成三棱柱，

故选：．

根据三棱柱的特点可得：侧面展开图是三个长方形，上下两个底面是两个全等的三角形．

此题主要考查了展开图折叠成几何体，关键是掌握几何体的展开图的特特点．

12.【答案】 

【解析】解：，，，

，

互不重合的、、三点在同一直线上，

若点在、之间，

则，

即，

解得，

故A情况存在，

若点在、之间，

则，

即，

解得，

故B情况不存在，

若点在、之间，

则，

即，

此时无解，

故C情况不存在，

故选：．

用假设法分别计算各选项中的值，根据判断即可．

本题主要考查两点间的距离及整式的加减，分类讨论和反证法的应用是解题的关键．

13.【答案】 

【解析】解：。

故答案为：。

根据度分秒的计算，度与度相减，分与分相减，进行计算即可得解。

本题考查了度、分、秒的减法计算，相对比较简单，注意以为进制即可。

14.【答案】 

【解析】解：、互为相反数，

，

、互为倒数，

，

．

故答案为：．

由、互为相反数可得，由、互为倒数可得，再代入所求的式子计算即可．

本题考查了相反数的定义、倒数的定义、有理数的加减和代数式求值，属于基础题型，熟练掌握基本知识是解题关键．

15.【答案】 

【解析】解：，，

，

多项式的最高次项为，最低次项为，

多项式的最高次项与最低次项的和为．

故答案为：．

先计算出，然后写出多项式的最高次项与最低次项的和即可．

本题考查整式的加减，解答本题的关键是明确去括号法则和合并同类项的方法．

16.【答案】 

【解析】解：实际售价为：，

所以，每件童装所得的利润为：．

故答案为：．

先表示出用每件童装的实际售价，然后减去进价就是利润的表达式．

本题考查了列代数式，解题的关键在于读懂题意，明白打六折的含义．

17.【答案】 

【解析】解：，

，

根据翻折前后两个角相等，．

故答案为：．

根据平角定义求出，再根据翻折的定义可得，计算即可得解．

本题主要考查了翻折的性质，熟记翻折前后两个角相等是解题的关键．

18.【答案】     

【解析】解：由图可知：，，

，

即：，

；

，

，

．

故答案为：，，．

根据点在数轴上的位置，确定取值范围，然后进行求解即可．

本题考查了利用数轴判断式子的正负，以及整式的加法，掌握数轴上点的位置，确定出式子的取值范围是关键．

19.【答案】解：，

移项，得：，

合并同类项，得：，

系数化，得：；

，

方程两边同乘，得：，

去括号，得：，

移项，得：，

合并同类项，得：，

系数化，得：． 

【解析】移项，合并同类项，系数化，解方程即可；

去分母，去括号，移项，合并同类项，系数化，解方程即可．

本题考查了解一元一次方程，掌握解一元一次方程的步骤，是关键．

20.【答案】解：原式

；

当，时，

原式． 

【解析】先去括号，再合并同类项，然后代值求解即可．

本题考查了整式加减中的化简求值，掌握合并同类项法则，正确的进行化是关键．

21.【答案】解：如图，、为所作；

如图，点为所作；

如图，点为所作；

两点之间，线段最短． 

【解析】

【分析】

本题考查了作图复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．

、根据几何语言画出对应的几何图形；

连接交于；

利用两点之间线段最短求解．

【解答】

解：见答案；

见答案；

见答案；

连接交于，则根据两点之间，线段最短可判断此时最小．

故答案为：两点之间，线段最短．  

22.【答案】  或 

【解析】解：是线段的中点，，

，

，

，

，

，

；

故答案为：；

由可知：，

当在线段上时，如图：

，

；

当在线段上时，如图：

，

；

综上：的长为：或．

故答案为：或．

利用是线段的中点，求出线段，再利用，得到，进而得到，利用，即可得解；

分在线段上，和在线段上，两种情况讨论，求解即可．

本题考查了线段的计算，掌握线段的中点将线段分成相等的两部分是关键．

23.【答案】或 

【解析】解：，

，

，

，

，

，

，

由题意得：，

；

由知方程的解，

，都是正整数，

是的倍数，且，

当时，，

当时，，

当时，，

当时，，

或．

故答案为：或．

分别求出关于的方程和的解，由题意得，即可求出的值；

分情况讨论，使方程的解和的值是正整数，即可求解．

本题考查同解方程，关键是求的值时，要分情况讨论．

24.【答案】解：，

，

，

平分，

． 

【解析】先求得，再由，结合平分可得答案．

本题考查了角平分线定义和角的有关计算，能求出的度数和得出是解此题的关键

25.【答案】解：把，，代入，得：，

整理，得：，

解得：；

解：把，代入，得：，

，

，

当时，的值为，

，即：，

；

当时，，，

，

． 

【解析】把，，代入等式中，求值即可；

把，代入等式，求解即可；

分别求出时，，的值，即可得解．

本题考查整式的加减，以及解一元一次方程．熟练掌握合并同类项法则，以及解一元一次方程的步骤，利用整体思想进行求解，是解题的关键．

26.【答案】或   

【解析】解：

如图，，与互补，

，

，

，

；

如图，，与互补，

，

，

，

；

的值为或；

故答案为：或；

，，

，

，

平分，

，

，

故答案为：；

存在，理由如下：

与互余，

，

，

，

，

；

与互余，

，

，

，

，

，

的值为或；

根据题意可知的位置有两种情况，分情况讨论计算的值；

读懂题意，确定，的位置，根据角平分线定义，角的和差，计算的度数；

读懂题意，根据的两种位置，分情况计算的值．

本题考查了互余角，互补角，角平分线，解题的关键是读懂题意，确定射线位置，分情况讨论解决问题．

27.【答案】    或 

【解析】解：由图可知：，

，

，

故答案为：；

由题意，得：，

由图可知：，，

分数的分子越大，分母越小，分数就越大，

，

，

故答案为：；

点是数轴上点、的“倍伴随点”，

，

，

设：点所表示的数为，

当在中间时：，解得：；

当在的右侧时：，解得：；

综上：点表示的数为：或；

故答案为：或；

设点表示的数为，

当在点左侧时，，，

点、分别为、的中点，

，

，

，

，

，

解得：，

，，

；

当在点右侧时，，，

点、分别为、的中点，

，

，

，

，

，

解得：，

，，

；

综上：，点表示的数为；点表示的数为．

求出，，根据“倍伴随点”的定义，进行求解即可；

根据定义，结合点在数轴上的位置，进行比较即可；

根据点是数轴上点、的“倍伴随点”，结合定义进行求解即可；

分在点左侧，和在点右侧，进行讨论求解即可．

本题考查了数轴上两点间的距离，一元一次方程的应用，掌握“倍伴随点”的定义是关键．