山东省济南市商河县2022-2023学年八年级下学期期末考试数学试卷(含解析)

2022-2023学年山东省济南市商河县八年级（下）期末数学试卷

一、选择题（本大题共10小题，共40.0分。在每小题列出的选项中，选出符合题目的一项）

1.  下列卡通图标分别是“星球”、“宇航员”、“星系”和“黑洞”，其中是中心对称图形的是(    )

A.  B.  C.  D.

2.  已知实数和，若，则下列结论中，不一定成立的是(    )

A.  B.  C.  D.

3.  在下列因式分解的过程中，分解因式正确的是(    )

A.  B.
C.  D.

4.  如果代数式的值为，那么实数满足(    )

A.  B.  C.  D.

5.  在中，，，的垂直平分线交于点，，则等于(    )

A.  B.  C.  D.

6.  已知，则(    )

A.  B.  C.  D.

7.  现有一四边形，借助此四边形作平行四边形，两位同学提供了如下方案，对于方案Ⅰ、Ⅱ，下列说法正确的是(    )

A. Ⅰ可行、Ⅱ不可行 B. Ⅰ不可行、Ⅱ可行
C. Ⅰ、Ⅱ都可行 D. Ⅰ、Ⅱ都不可行

8.  如图，平移图形，与图形可以拼成一个平行四边形，则图中的度数为(    )

A.  B.  C.  D.

9.  如图，在中，，，将绕点逆时针方向旋转到的位置，则图中阴影部分的面积是(    )

A.
B.
C.
D.

10.  如图，中，，，，点为上任意一点，连接，以、为邻边作平行四边形，连接，与交于点，则的最小值为(    )

A.
B.
C.
D.

二、填空题（本大题共5小题，共20.0分）

11.  若，，则 ______ ．

12.  若，则分式 ______ ．

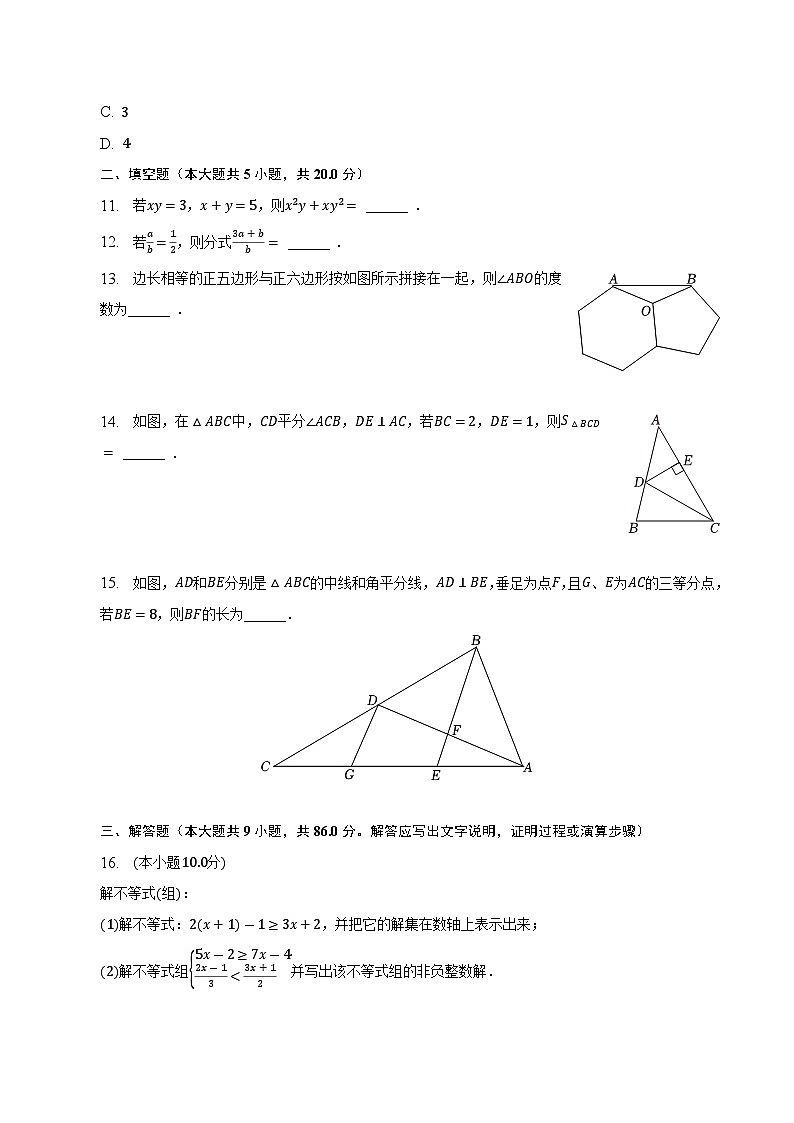
13.  边长相等的正五边形与正六边形按如图所示拼接在一起，则的度数为______ ．

14.  如图，在中，平分，，若，，则 ______ ．

15.  如图，和分别是的中线和角平分线，，垂足为点，且、为的三等分点，若，则的长为______．

三、解答题（本大题共9小题，共86.0分。解答应写出文字说明，证明过程或演算步骤）

16.  本小题分
解不等式组：
解不等式：，并把它的解集在数轴上表示出来；
解不等式组并写出该不等式组的非负整数解．

17.  本小题分
分解因式：
；
．

18.  本小题分
计算：
；
先化简，再求值，其中．

19.  本小题分
如图，平行四边形中，是直线上两点，且求证：．

20.  本小题分
如图，在平面直角坐标系中，点的坐标是，点的坐标是．
将先向下平移个单位长度，再向左平移个单位长度后得到，画出，并直接写出点的坐标；
将绕点逆时针旋转后得到，画出，并直接写出点的坐标；
求中扫过的面积．

21.  本小题分
王老师安排喜欢探究问题的小明同学解决某个问题前，先让小明看了一个有解答过程的例题．
例：若，求和的值．
解：，
．
即，
，，
，．
为什么要对进行了拆项呢？聪明的小明理解了例题解决问题的方法，很快解决了下面两个问题相信你也能很好的解决下面的这两个问题，请写出你的解题过程．
若，求的值；
已知、、是等腰的三边长，且满足，求此三角形的周长．

22.  本小题分
如图，在中，，点在上运动，点在上运动，始终保持与相等，的垂直平分线交于点，交于点，连接．
判断与的位置关系，并说明理由；
若，，，求线段的长．

23.  本小题分
李老师近期准备换车，看中了价格相同的两款国产车经过对某款电动汽车和某款燃油车的对比调查发现，电动汽车平均每公里的行驶费用比燃油车平均每公里的行驶费用少元若两款车的行驶费用均为元时，电动汽车可行驶的总路程是燃油车的倍．
求这款电动汽车平均每公里的行驶费用；
若电动汽车和燃油车每年的其它费用分别为元和元问：每年行驶里程为多少千米时，买电动汽车的年费用更低？年费用年行驶费用年其它费用

24.  本小题分
综合与实践
图形的旋转变换是研究数学相关问题的重要手段之一，在研究三角形的旋转过程中，发现下列问题：如图，在中，，，，分别为，边上一点，连接，且，将绕点在平面内旋转．
观察猜想
若，将绕点旋转到如图所示的位置，则与的数量关系为______；
类比探究
若，将绕点旋转到如图所示的位置，，相交于点，猜想，满足的位置关系，并说明理由；
拓展应用
如图，在的条件下，连结，分别取，，的中点，，，连结，，，若，，请直接写出在旋转过程中面积的最大值．

答案

1.答案： 

解：选项A、、均不能找到一个点，使图形绕某一点旋转后与原来的图形重合，所以不是中心对称图形；
选项D能找到一个点，使图形绕某一点旋转后与原来的图形重合，所以是中心对称图形．
故选：．
 

2.答案： 

解：，
，原变形正确，故本选项不符合题意；
B.，
，必须规定，原变形不一定正确，故本选项符合题意；
C.，
，原变形正确，故本选项不符合题意；
D.，
，原变形正确，故本选项不符合题意；
故选：．
 

3.答案： 

解：、原式不能分解，不符合题意；
B、原式，不符合题意；
C、原式，符合题意；
D、原式不能分解，不符合题意，
故选：．
 

4.答案： 

解：代数式的值为，
且，
解得，
故选：．
 

5.答案： 

解：，，垂直平分，
，
，
，
又，
为等腰三角形，
，
故选：．
 

6.答案： 

解：把两边平方得：，
则，
故选：．  

7.答案： 

解：方案Ⅰ：连接，
，，，是边，，，的垂直平分线，
和分别是和的中位线，
，，，，
，，
四边形是平行四边形；
方案Ⅱ：
，，
，，
四边形是平行四边形．
故选：．
 

8.答案： 

解：四边形是平行四边形，

，
，
故选：．
 

9.答案： 

解：，，
，
将绕点逆时针方向旋转到的位置，
，，
是等边三角形，
图中阴影部分的面积，
图中阴影部分的面积，
故选：．
 

10.答案： 

解：，，，
，，
四边形是平行四边形，
，，
最短也就是最短，
过作的垂线，
，，
∽，
，
，
，
则的最小值为．
故选：．
 

11.答案： 

解：，，
．
故答案为：．
 

12.答案： 

解：，
，
；
故答案为：．
 

13.答案： 

解：由题意得：正六边形的每个内角都等于，正五边形的每个内角都等于，
，
，
，
故答案为：．
 

14.答案： 

解：过点作于点，如图所示．
平分，，
．


．
故答案为：．
 

15.答案： 

解：，，
是的中位线，
，，
在和中，
，
≌
，
，，
，
，
故答案是：．
16.解：，
，
，
，
则，
将解集表示在数轴上如下：

由得：，
由得：，
则不等式组的解集为，
所以不等式组的非负整数解为、． 

17.解：；


． 

18.解：



；




，
当时，原式． 

19.证明：四边形是平行四边形，
，，
．
，
≌，
，
． 

20.答案：解：如图，为所作，点的坐标为；
如图，为所作，点的坐标为；

，
所以扫过的面积 

21.解：，
，
即，
，，
解得，，
；
，
，
，，
，，
当为腰长时，，，能组成三角形，的周长；
当为腰长时，，，能组成三角形，的周长．
此三角形的周长为或． 

22. 解：，
理由如下：，
，
是的垂直平分线，
，
，
，
，
，
，
；
连接，设，则，，
，
，
，
解得：，
则． 

23.解：设这款电动汽车平均每公里的行驶费用为元，则燃油车平均每公里的行驶费用为元，
根据题意得：，
解得：，
经检验，是所列方程的解，且符合题意．
答：这款电动汽车平均每公里的行驶费用为元；
燃油车平均每公里的行驶费用为元．
设每年行驶里程为，
根据题意得：，
解得：．
答：当每年行驶里程大于时，买电动汽车的年费用更低． 

24. 

解：如图，，
，
，
，，
，
，
旋转，
，
又，，
≌，
，
故答案为：；
，
理由如下：如图，设与的交点为点，

绕点旋转到如图所示的位置，，
，
，
在与中，
，
≌，
，
是的外角，也是的外角，
，
，
；
，，分别是，，的中点，
，，，，
≌，
，
，
，，，
，
是等腰直角三角形，
的面积，
，，
当点，点，点三点共线时，有最大值，即面积有最大值，
的最大值为，面积的最大值为．