
2022-2023学年山东省济南市槐荫区八年级(下)期末数学试卷(含解析)
展开2022-2023学年山东省济南市槐荫区八年级(下)期末数学试卷
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. 下列图形是中心对称图形的是( )
A. B.
C. D.
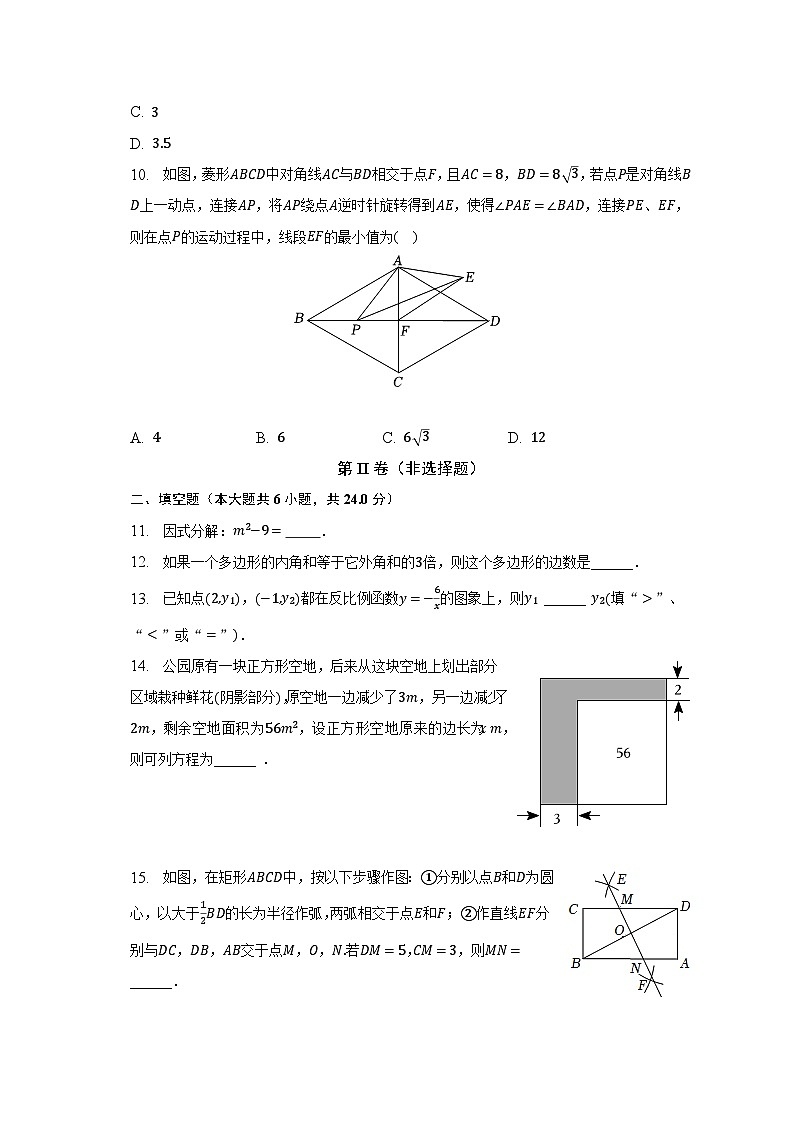
2. 如图所示,该几何体的俯视图是( )
A.
B.
C.
D.
3. 反比例函数y=kx的图象经过点(−6,1),则此函数的图象也经过点( )
A. (−3,−3) B. (−4,6) C. (2,3) D. (2,−3)
4. 计算mm−1+11−m的结果是( )
A. 1 B. −1 C. 2 D. −2
5. 下列性质中,是矩形的性质的是( )
A. 对角线互相垂直 B. 对角线相等
C. 四边相等 D. 对角线平分一组对角
6. 若关于x的一元二次方程x2−6x+m=0有实数根,则实数m的取值范围是( )
A. m<9 B. m≤9 C. m>9 D. m≥9
7. 在同一平面直角坐标系中,函数y=kx−k(k≠0)与y=kx(k≠0)的大致图象可能是( )
A. B.
C. D.
8. 如图,将△ABC绕点A逆时针旋转55°得到△ADE,若∠E=75°且AD⊥BC于点F,则∠BAC的度数为( )
A. 65° B. 70° C. 75° D. 80°
9. 如图,点A是反比例函数y=−2x在第二象限内图象上一点,点B是反比例函数y=4x在第一象限内图象上一点,直线AB与y轴交于点C,且AC=BC,连接OA、OB,则△AOB的面积是( )
A. 2
B. 2.5
C. 3
D. 3.5
10. 如图,菱形ABCD中对角线AC与BD相交于点F,且AC=8,BD=8 3,若点P是对角线BD上一动点,连接AP,将AP绕点A逆时针旋转得到AE,使得∠PAE=∠BAD,连接PE、EF,则在点P的运动过程中,线段EF的最小值为( )
A. 4 B. 6 C. 6 3 D. 12
第II卷(非选择题)
二、填空题(本大题共6小题,共24.0分)
11. 因式分解:m2−9= .
12. 如果一个多边形的内角和等于它外角和的3倍,则这个多边形的边数是______.
13. 已知点(2,y1),(−1,y2)都在反比例函数y=−6x的图象上,则y1 ______ y2(填“>”、“<”或“=”).
14. 公园原有一块正方形空地,后来从这块空地上划出部分区域栽种鲜花(阴影部分),原空地一边减少了3m,另一边减少了2m,剩余空地面积为56m2,设正方形空地原来的边长为x m,则可列方程为______ .
15. 如图,在矩形ABCD中,按以下步骤作图:①分别以点B和D为圆心,以大于12BD的长为半径作弧,两弧相交于点E和F;②作直线EF分别与DC,DB,AB交于点M,O,N.若DM=5,CM=3,则MN=______.
16. 将等腰直角三角形ABC沿AC折叠,得到△ADC,连接BD并延长于点P,连接PA,过点P作PA⊥PE交BC的延长线于点E,若AB=2,PA= 10,则BE= ______ .
三、解答题(本大题共10小题,共86.0分。解答应写出文字说明,证明过程或演算步骤)
17. (本小题6.0分)
解方程:x2−4x−5=0.
18. (本小题6.0分)
计算:2aa2−4−1a−2.
19. (本小题6.0分)
如图,E、F是正方形ABCD的对角线AC上的两点,BE//DF.求证:AE=CF.
20. (本小题8.0分)
如图,在▱ABCD中,∠D=60°,AE⊥BC,AF⊥CD,垂足分别为点E、F.
(1)求∠EAF的度数.
(2)若▱ABCD的面积为80 3,AB=10,求CF的长.
21. (本小题8.0分)
在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,图①、图②、图③均为顶点都在格点上的三角形(每个小方格的顶点叫格点),
(1)在图1中,图①经过一次______变换(填“平移”或“旋转”或“轴对称”)可以得到图②;
(2)在图1中,图③是可以由图②经过一次旋转变换得到的,其旋转中心是点______(填“A”或“B”或“C”);
(3)在图2中画出图①绕点A顺时针旋转90°后的图④.
22. (本小题8.0分)
一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件,
(1)若降价a元,则平均每天销售数量为____件(用含a的代数式表示):
(2)当每件商品降价多少元时,该商店每天销售利润为1200元?
23. (本小题10.0分)
槐荫区大力推动“书香校园”建设,为了深入实施中华经典诵读工程,某校开展名著诵读活动,李老师推荐了4种不同的名著A,B,C,D.甲,乙两位同学分别从中任意选一种阅读,假设选任意一种都是等可能的.
(1)甲同学选中名著A的概率是______ .
(2)求甲、乙两位同学恰好选同一种名著的概率.
24. (本小题10.0分)
如图,在四边形ABCD中,∠A=90°,AD//BC,点E在AD边上,连接BE、BD,若EB=BC,BD平分∠EBC.
(1)如图1,求证:四边形EBCD是菱形;
(2)如图2,连接CE交BD于点O,连接AO,若EC=BC,在不添加任何辅助线的情况下,请直接写出图2中长度等于 3OC的线段.
25. (本小题12.0分)
如图1,点A(m,6),B(6,1)在反比例函数y=kx上,作直线AB,交坐标轴于点M、N,连接OA、OB.
(1)求反比例函数的表达式和m的值;
(2)求△AOB的面积;
(3)如图2,E是线段AB上一点,作AD⊥x轴于点D,过点E作EF//AD,交反比例函数图象于点F,若EF=13AD,求出点E的坐标.
26. (本小题12.0分)
已知,四边形ABCD是正方形,△DEF绕点D旋转(DE
(2)直线AE与CF相交于点G.
①如图2,BM⊥AG于点M,BN⊥CF于点N,求证:四边形BMGN是正方形;
②如图3,连接BG,若AB=5,DE=3,直接写出在△DEF旋转的过程中,线段BG长度的最小值.
答案和解析
1.【答案】A
【解析】解:选项B、C、D都不能找到这样的一个点,使图形绕某一点旋转180°后与原来的图形重合,所以不是中心对称图形,
选项A能找到这样的一个点,使图形绕某一点旋转180°后与原来的图形重合,所以是中心对称图形,
故选:A.
根据中心对称图形的概念判断.把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形.
本题考查的是中心对称图形,中心对称图形是要寻找对称中心,旋转180度后与自身重合.
2.【答案】A
【解析】
【分析】
找到从上面看所得到的图形即可,注意看见的棱用实线表示.
本题考查了三视图的知识,俯视图是从物体的上面看得到的视图.
【解答】
解:从上面看可得到一个正方形,正方形里面有一条斜实线,如图所示:.
故选:A.
3.【答案】D
【解析】解:∵反比例数解析式为y=kx,图象经过点(−6,1),代入得:1=k−6,
解得:k=−6,
∴反比例函数解析式为:y=−6x,
A.∵(−3)×(−3)=9≠−6,
∴(−3,−3)不在反比例函数y=−6x上,故该选项不正确,不符合题意;
B.∵−4×6=−24≠−6,
∴(−4,6)不在反比例函数y=−6x上,故该选项不正确,不符合题意;
C.∵2×3=6≠−6,
∴(2,3)不在反比例函数y=−6x上,故该选项不正确,不符合题意;
D.∵2×(−3)=−6,
∴(2,−3)在反比例函数y=−6x上,故该选项正确,符合题意;
故选:D.
根据题意求得k=−6,然后分别计算各选项即可求解.
本题考查了反比例函数的性质,掌握反比例函数的性质是解题的关键.
4.【答案】A
【解析】解:原式=mm−1−1m−1=m−1m−1=1,
故选:A.
原式变形后,利用同分母分式的减法法则计算即可得到结果.
此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.
5.【答案】B
【解析】解:A.矩形的对角线相等但不一定垂直,故本选项符合题意;
B.矩形的对角线相等,故本选项符合题意;
C.矩形的邻边不一定相等,故本选项不符合题意;
D.矩形对角线互相平分但一条对角线不一定平分一组对角,故本选项符合题意;
故选:B.
根据矩形的边的特征,对角线的特征,来判断即可.
本题主要考查了矩形的性质,熟记矩形的性质是解决问题的关键.
6.【答案】B
【解析】解:∵关于x的一元二次方程x2−6x+m=0有实数根,
∴Δ=(−6)2−4×1×m≥0,
∴m≤9.
故选:B.
根据方程的系数结合根的判别式Δ=b2−4ac≥0,即可得出关于m的一元一次不等式,解之即可得出m的取值范围.
本题考查了根的判别式,牢记“当Δ≥0时,方程有实数根”是解题的关键.
7.【答案】C
【解析】解:①当k>0时,y=kx−k过一、三、四象限;函数y=kx(k≠0)的图象过一、三象限;
②当k<0时,y=kx−k过一、二、四象象限;函数y=kx(k≠0)的图象过二、四象限.
观察图形可知,只有C选项符合题意.
故选:C.
分两种情况讨论,当k>0时,分析出一次函数和反比例函数所过象限;再分析出k<0时,一次函数和反比例函数所过象限,符合题意者即为正确答案.
本题主要考查了反比例函数的图象和一次函数的图象,熟悉两函数中k的符号对函数图象的影响是解题的关键.
8.【答案】B
【解析】解:∵将△ABC绕点A逆时针旋转55°得△ADE,
∴∠BAD=55°,∠E=∠ACB=75°,
∵AD⊥BC,
∴∠DAC=15°,
∴∠BAC=∠BAD+∠DAC=70°.
故选:B.
由旋转的性质可得∠BAD=55°,∠E=∠ACB=75°,由直角三角形的性质可得∠DAC=15°,即可求解.
本题考查了旋转的性质,掌握旋转的性质是本题的关键.
9.【答案】C
【解析】解:分别过A、B两点作AD⊥x轴,BE⊥x轴,垂足为D、E,
∵AC=CB,
∴OD=OE,
设A(−a,2a),则B(a,4a),
故S△AOB=S梯形ADBE−S△AOD−S△BOE=12(2a+4a)×2a−12a×2a−12a×4a=3.
故选:C.
分别过A、B两点作x轴的垂线,构成直角梯形,根据AC=BC,判断OC为直角梯形的中位线,得出OD=OE=a,根据双曲线解析式确定A、B两点的坐标及AD、BE的长,根据S△AOB=S梯形ADBE−S△AOD−S△BOE求解.
本题考查了反比例函数的综合运用,关键是作辅助线构造直角梯形,根据AC=BC,得出OC为直角梯形的中位线,利用面积的和差关系求解.
10.【答案】B
【解析】解:连接DE,
∵四边形ABCD是菱形,且AC=8,BD=8 3,
∴AF=12AC=4,DF=12BD=4 3,
∵AC⊥BD,BA=DA,
∴AD= AF2+DF2= 42+(4 3)2=8,
∴∠ADB=∠ABD=30°,
将AP绕点A逆时针旋转使得∠PAE=∠BAD,
∴AP=AE,∠BAD=∠PAE
∴∠BAP=∠DAE
在△BAP和△DAE中,
BA=DA∠BAP=DAEPA=AE,
∴△BAP≌△DAE(SAS),
∴∠ADE=∠ABP=30°,
∴∠ABD+∠ADE=60°,
∴当EF⊥DE时EF最小,
此时∠EFD=30°,
∴EF=DF×cos∠EFD=4 3× 32=6.
故选:B.
连接DE,由菱形的性质及AC=8,BD=8 3得出AF=4,DF=4 3,AC⊥DB,AB=AD,由勾股定理得AD=8,进而得出,∠ADB=∠ABD=30°,证明三角形PAB全等于三角形EDA,得出角ADE=30°,得出当EF⊥DE时EF最小.求出EF的长度即可.
本题考查了菱形的性质,旋转的性质,特殊角的三角函数值三角函数的值,找出全等的三角形证明∠ADE=30°是关键.
11.【答案】(m+3)(m−3)
【解析】
【分析】
直接利用平方差公式分解因式得出答案.
此题主要考查了公式法分解因式,正确运用平方差公式是解题关键.
【解答】
解:m2−9=m2−32
=(m+3)(m−3).
故答案为:(m+3)(m−3).
12.【答案】8
【解析】解:多边形的外角和是360°,根据题意得:
180°⋅(n−2)=3×360°
解得n=8.
故答案为:8.
根据多边形的内角和公式及外角和计算.
本题主要考查了多边形内角和公式及外角的和.求多边形的边数,可以转化为方程的问题来解决.
13.【答案】<
【解析】解:∵反比例函数y=−6x的图象分布在二四象限,点(2,y1)在四象限,在x轴下方;点(−1,y2)在二象限,在x轴上方,
∴y1
根据反比例函数的性质,k<0,图象分布在二四象限,根据点所在象限即可判断出y1、y2的大小.
本题考查了反比例函数的性质,数形结合是这类题目的突破口.
14.【答案】(x−3)(x−2)=56
【解析】解:由图可得,
(x−3)(x−2)=56,
故答案为:(x−3)(x−2)=56.
根据题目中的数据和图形,可以得到方程(x−3)(x−2)=56,本题得以解决.
本题考查由实际问题抽象出一元二次方程,解答本题的关键是明确题意,列出相应的方程.
15.【答案】2 5
【解析】解:如图,连接BM.
由作图可知MN垂直平分线段BD,
∴BM=DM=5,
∵四边形ABCD是矩形,
∴∠C=90°,CD//AB,
∴BC= BM2−CM2= 52−32=4,
∴BD= CB2+CD2= 42+82=4 5,
∴OB=OD=2 5,
∵∠MOD=90°,
∴OM= DM2−OD2= 52−(2 5)2= 5,
∵CD//AB,
∴∠MDO=∠NBO,
在△MDO和△NBO中,
∠MDO=∠NBOOD=OB∠MOD=∠NOB,
∴△MDO≌△NBO(ASA),
∴OM=ON= 5,
∴MN=2 5.
故答案为:2 5.
如图,连接BM.利用勾股定理求出BC,BD,OM,再证明OM=ON,可得结论.
本题考查了作图−基本作图、线段垂直平分线的性质、勾股定理、矩形的性质,解决本题的关键是掌握线段垂直平分线的性质.
16.【答案】4
【解析】解:∵AB=CB,∠ABC=90°,
∴∠BAC=∠BCA=45°,
由折叠得∠DAC=∠BAC=45°,∠DCA=∠BCA=45°,
∴∠BAD=∠BCD=∠ABC=90°,
∴四边形ABCD是矩形,
∴四边形ABCD是正方形,
∴AC=BD,AC⊥BD,
∴∠ABD=∠CBD=45°,
设AC交BD于点F,
∵AD=AB=2,
∴AC=BD= AB2+AD2= 22+22=2 2,
∴AF=CF=12AC= 2,BF=DF=12BD= 2,
∵∠AFP=90°,AP= 10,
∴PF= AP2−AF2= ( 10)2−( 2)2=2 2,
∴BP=BF+PF= 2+2 2=3 2,
作PG⊥BA交BA的延长线于点G,PH⊥BE于点H,则∠G=∠PHB=90°,
∴四边形PGBH是矩形,∠PHE=∠G=90°,
∵PG=PH,
∴四边形PGBH是正方形,
∴∠GPH=90°,
∵PA⊥PE,
∴∠APE=90°,
∴∠EPH=∠APG=90°−∠APH,
在△EPH和△APG中,
∠PHE=∠GPH=PG∠EPH=∠APG,
∴△EPH≌△APG(ASA),
∵G=90°,GP=GB,
∴GP2+GB2=2GB2=BP2,
∴2GB2=(3 2)2,
解得GB=3或GB=−3(不符合题意,舍去),
∴HB=GB=3,EH=AG=3−2=1,
∴BE=HB+EH=3+1=4,
故答案为:4.
先证明四边形ABCD是正方形,得AC=BD,AC⊥BD,则∠ABD=∠CBD=45°,设AC交BD于点F,由AD=AB=2,得AC=BD= AB2+AD2=2 2,则AF=CF=BF=DF= 2,由勾股定理得PF= AP2−AF2=2 2,则BP=3 2,作PG⊥BA交BA的延长线于点G,PH⊥BE于点H,可证明四边形PGBH是正方形,则∠GPH=90°,而∠APE=90°,所以∠EPH=∠APG=90°−∠APH,可证明△EPH≌△APG,由2GB2=(3 2)2,求得GB=3,则HB=GB=3,EH=AG=1,所以BE=HB+EH=4,于是得到问题的答案.
此题重点考查正方形的判定与性质、全等三角形的判定与性质、勾股定理等知识,正确地作出所需要的辅助线是解题的关键.
17.【答案】解:(x+1)(x−5)=0,
则x+1=0或x−5=0,
∴x1=−1,x2=5.
【解析】根据本题方程的特点,利用因式分解法解方程即可.
本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键
18.【答案】解:原式=2a(a+2)(a−2)−1a−2
=2a(a+2)(a−2)−a+2(a+2)(a−2)
=2a−(a+2)(a+2)(a−2)
=a−2(a+2)(a−2)
=1a+2.
【解析】先通分变成同分母的分式,再根据同分母的分式相加减的法则进行计算即可.
本题考查了分式的加减法,能灵活运用法则进行计算是解此题的关键,注意:结果化成最简分式或整式.
19.【答案】证明:∵四边形ABCD是正方形,
∴AB=CD,AB//CD,
∠BAE=∠DCF,
∵BE//DF,
∴∠BEC=∠DFA,
∴∠AEB=∠CFD,
在△ABE和△CDF中,
∠AEB=∠CFD∠BAE=∠DCFAB=CD,
∴△ABE≌△CDF(AAS),
∴AE=CF.
【解析】本题主要考查了正方形的性质,全等三角形性质和判定,熟练掌握正方形的性质和全等三角形的判定是解决问题的关键.
先证∠AEB=∠CFD,再根据AAS证△ABE≌△CDF,从而得出AE=CF.
20.【答案】解:(1)∵四边形ABCD是平行四边形,
∴AB//CD,∠B=∠D=60°,
∴∠B+∠C=180°,
∵∠B=60°,
∴∠C=120°,
∵AE⊥BC,AF⊥CD,
∴∠AEC=∠AFC=90°,
在四边形AECF中,∠EAF+∠AEC+∠C+∠AFC=360°,
∴∠EAF=60°;
(2)∵四边形ABCD是平行四边形,
∴DC=AB=10,
∵▱ABCD的面积为80 3,
∴10×AF=80 3,
∴AF=8 3,
∵∠D=60°,
∴tan60°=AFDF= 3,
∴DF=8,
∴CF=CD−DF=10−8=2,
∴CF=2.
【解析】(1)利用平行四边形的邻角互补的知识先求出∠C的度数,然后利用四边形的内角和定理即可求出∠EAF的度数.
(2)根据平行四边形的性质得出CD的长,根据面积求出AF的长,进而利用三角函数得出DF的长,最后根据线段的和差关系解答即可.
此题考查了平行四边形及三角函数的知识,要求我们掌握平行四边形的邻角互补及锐角三角函数.
21.【答案】(1)平移;
(2) A;
(3)如图.
【解析】解:(1)图①经过一次平移变换可以得到图②;
故答案为:平移;
(2)图③是可以由图②经过一次旋转变换得到的,其旋转中心是点A;
故答案为:A;
(3)见答案.
(1)根据平移的定义可知图①向右、向上平移可以得到图②;
(2)将图形②绕着点A旋转后能与图形③重合,可知旋转中心;
(3)以A为旋转中心,顺时针旋转90°得到关键顶点的对应点连接即可.
本题难度中等,考查网格中平移、旋转及旋转作图,作图时,抓住网格的特点,根据旋转的性质,借助于直角三角板中的直角,就能顺利作出图形,解题时要注意是顺时针还是逆时针方向.
平移是沿直线移动一定距离得到新图形,旋转是绕某个点旋转一定角度得到新图形,观察时要紧扣图形变换特点,认真判断.
22.【答案】(1)2a+20;
(2)设每件商品降价x元,
根据题意得:(40−x)(20+2x)=1200,
解得:x1=10,x2=20,
40−10=30>25(符合题意),
40−20=20<25(舍去),
答:当每件商品降价10元时,该商店每天销售利润为1200元.
【解析】
【分析】
本题考查了一元二次方程的应用,正确找出等量关系,列出一元二次方程是解题的关键.
(1)根据“平均每天可售出20件,每件盈利40元,销售单价每降低1元,平均每天可多售出2件,若降价a元”,列出平均每天销售的数量即可;
(2)设每件商品降价x元,根据“平均每天可售出20件,每件盈利40元,销售单价每降低1元,平均每天可多售出2件,每件盈利不少于25元”列出关于x的一元二次方程,解之,根据实际情况,找出盈利不少于25元的答案即可.
【解答】
解:(1)根据题意得:
若降价a元,则多售出2a件,
平均每天销售数量为:2a+20,
故答案为:2a+20;
(2)见答案.
23.【答案】14
【解析】解:(1)共有A,B,C,D4种不同的名著,从中任意选一种,选任意一种都是等可能的.
所以选中名著A的概率是14,
故答案为:14;
(2)甲、乙两位同学从A,B,C,D4种不同的名著中任意选一种,所有等可能出现的结果如下:
共有16种等可能出现的结果,其中甲、乙两位同学恰好选同一种名著的有4种,
所以甲、乙两位同学恰好选同一种名著的概率为416=14.
(1)根据概率的定义进行解答即可;
(2)用树状图表示所有等可能出现的结果,再根据概率的定义进行计算即可.
本题考查列表法或树状图法,列举出所有等可能出现的结果是正确解答的前提.
24.【答案】(1)证明:∵AD//BC,
∴∠ADB=∠DBC,
∵BD平分∠EBC,
∴∠EBD=∠DBC,
∴∠EBD=∠EDB,
∴EB=ED,
∵EB=BC,
∴ED=BC,
∵ED//BC,
∴四边形EBCD是平行四边形,
∵EB=BC,
∴平行四边形EBCD是菱形;
(2)解:如图2,∵平行四边形EBCD是菱形,
∴BE=BC=ED,BD⊥CE,BO=DO,∠CBO=∠EBO,
∵EC=BC,
∴EC=BC=BE,
∴△BCE是等边三角形,
∴∠BCE=∠CBE=60°,
∴tan∠BCO=OCOB= 3,
∴OB=OD= 3OC;
∵∠BAD=90°,
∴OA=OB=OD= 3OC;
∵∠CBO=∠EBO=12∠CBE=30°,
∵EB=ED,
∴∠EBO=∠EDO=30°,
∵OA=OD,
∴∠OAD=∠EDO=30°,
∴∠AOB=∠OAD=∠EDO=60°,
∴△ABO是等边三角形,
∴AB=OB= 3OC;
∴图2中长度等于 3OC的线段的线段是OA、OB、OD、AB.
【解析】(1)根据平行线性质得到∠ADB=∠DBC,根据角平分线的定义得到∠EBD=∠DBC,得到EB=ED,根据菱形的判定定理即可得到结论;
(2)根据菱形的性质得到BE=BC=ED,BD⊥CE,BO=DO,∠CBO=∠EBO,根据等边三角形的性质得到∠BCE=∠CBE=60°,根据三角函数的定义得到OB=OD= 3OC;根据直角三角形的性质即可得到结论.
本题考查了菱形的性质,等腰三角形的判定和性质,等边三角形的判定和性质,熟练掌握菱形的性质定理是解题的关键.
25.【答案】解:(1)设反比例函数的解析式为y=kx,
将B(6,1)的坐标代入y=kx,得k=6.
∴反比例函数的解析式为y=6x.
将A(m,6)的坐标代入y=6x,得m=1.
(2)如图1,设直线AB的解析式为y=ax+b,
把A(1,6)和B(6,1)代入上式,得:
a+b=66a+b=1,
解得:a=−1b=7,
故直线AB的解析式为:y=−x+7,
∴M(0,7),N(7,0),
∴S△AOB=S△MON−S△AOM−S△BON=12OM×ON−12OM×|xA|−12ON×|yB|
=12×7×7−12×7×1−12×7×1
=352.
(3)设E点的坐标为(m,−m+7),则F(m,6m),
∴EF=−m+7−6m.
∵EF=13AD,
∴−m+7−6m=13×6.
解得m1=2,m2=3,
经检验,m1=2,m2=3是分式方程的根,
∴E的坐标为(2,5)或(3,4).
【解析】(1)设反比例函数的解析式为y=kx,根据题意B点坐标得出k的值以及m的值;
(2)设直线AB的解析式为y=ax+b,求出直线AB的解析式,再利用S△AOB=S△MON−S△AOM−S△BON,求出答案即可;
(3)设E点的横坐标为m,则E(m,−m+7),F(m,6m),求出EF=−m+7−6m,得出关于m的方程,求出m即可.
本题考查了用待定系数法求出反比例函数和一次函数的解析式,正确得出直线AB的解析式是解题关键.
26.【答案】(1)证明:∵四边形ABCD是正方形,
∴AD=DC,∠ADC=90°,
∵DE=DF,∠EDF=90°,
∴∠ADC=∠EDF,
∴∠ADE=∠CDF,
∴△ADE≌△CDF(SAS);
(2)①证明:如图,设AG与CD相交于点P.
∠ADP=90°,
∠DAP+∠DPA=90°,
∵△ADE≌△CDF,
∴∠DAE=∠DCF.
∵∠DPA=∠GPC,
∴∠DAE+∠DPA=∠GPC+∠GCP=90°.
∠PGN=90°,
∵BM⊥AG,BN⊥GN,
∴四边形BMGN是矩形,
∴∠MBN=90°
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠MBN=90°.
∴∠ABM=∠CBN.
又∵∠AMB=∠BNC=90°
∴△AMB≌△CNB(ASA).
∴MB=NB.
∴矩形BMGN是正方形;
②解:作DH⊥AG交AG于点H,作BM⊥AG于点M,
此时△AMB≌△AHD.
∴BM=AH,
AH2=AD2−DH2,AD=5,
∴DH最大时,AH最小,DH=DE=3,
∴BM=AH=4,
由(2)①可知,△BGM是等腰直角三角形,
∴BG最小= 2BM=4 2.
【解析】(1)根据SAS证明三角形全等即可;
(2)①根据邻边相等的矩形是正方形证明即可;
②作DH⊥AG交AG于点H,作BM⊥AG于点M,证明△BMG是等腰直角三角形,求出BM的最小值,可得结论.
本题属于四边形综合题,考查了正方形的性质,全等三角形的判定和性质,等腰直角三角形的判定和性质,勾股定理等知识,解题的关键是正确寻找全等三角形解决问题,属于中考压轴题.
2022-2023学年山东省济南市槐荫区九年级(上)期末数学试卷(含解析): 这是一份2022-2023学年山东省济南市槐荫区九年级(上)期末数学试卷(含解析),共23页。试卷主要包含了选择题,四象限,计算题,解答题等内容,欢迎下载使用。
2022-2023学年山东省济南市槐荫区八年级(下)期末数学试卷(含解析): 这是一份2022-2023学年山东省济南市槐荫区八年级(下)期末数学试卷(含解析),共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年山东省济南市槐荫区七年级(下)期末数学试卷(含解析): 这是一份2022-2023学年山东省济南市槐荫区七年级(下)期末数学试卷(含解析),共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。













