北师大版九年级下册1 锐角三角函数背景图课件ppt

这是一份北师大版九年级下册1 锐角三角函数背景图课件ppt，共21页。PPT课件主要包含了新课导入，探究新知，例题详解，解甲梯中，乙梯中，随堂练习等内容，欢迎下载使用。

猜一猜，这座古塔有多高？
想一想，你能运用所学的数学知识测出这座古塔的高吗？
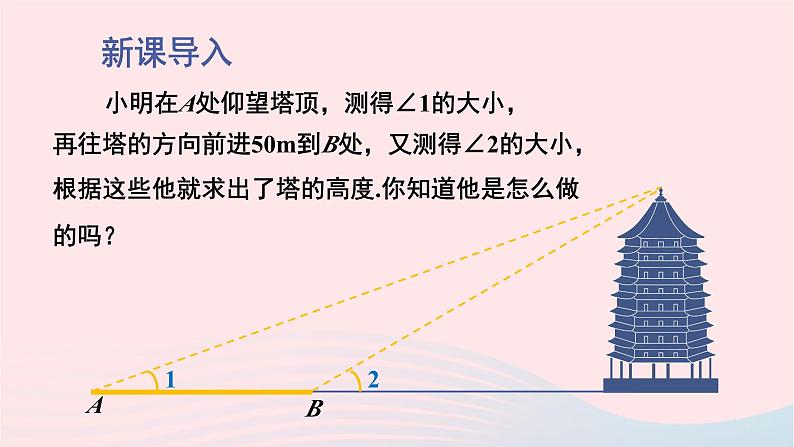
小明在A处仰望塔顶，测得∠1的大小，
再往塔的方向前进50m到B处，又测得∠2的大小，
根据这些他就求出了塔的高度.你知道他是怎么做的吗？
本章我们将借助生活中的实例，探索直角三角形边角之间的关系，并利用三角函数解决生活中一些简单的实际问题.
梯子是我们日常生活中常见的物体.
你能比较两个梯子那个更陡吗？你有哪些方法？
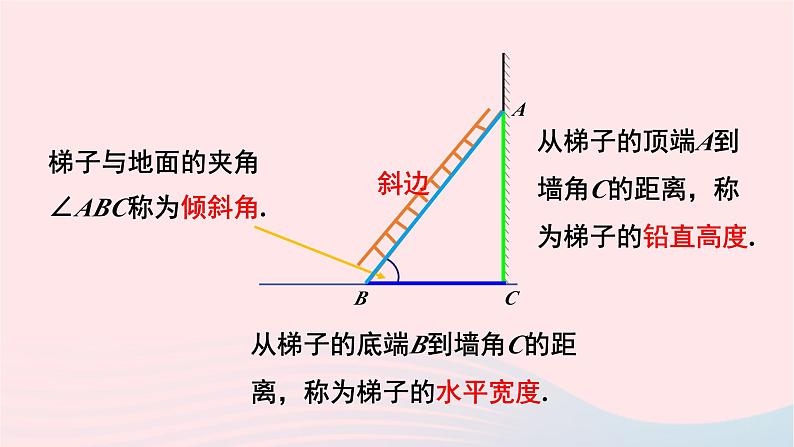
梯子与地面的夹角∠ABC称为倾斜角.
从梯子的顶端A到墙角C的距离，称为梯子的铅直高度.
从梯子的底端B到墙角C的距离，称为梯子的水平宽度.
梯子在上升变陡过程中，倾斜角的大小有无变化？如何变化？
倾斜角越大——梯子越陡
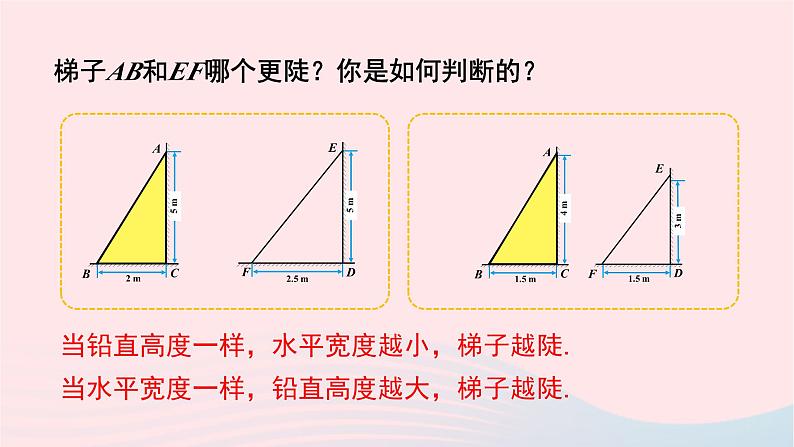
梯子AB和EF哪个更陡？你是如何判断的？
当铅直高度一样，水平宽度越小，梯子越陡.
当水平宽度一样，铅直高度越大，梯子越陡.
如图，小明想通过测量B1C1及AC1 ，算出它们的比，来说明梯子AB1的倾斜程度；
小亮认为，通过测量B2C2及AC2 ，算出它们的比，也能说明梯子AB1的倾斜程度.
你同意小亮的看法吗？
（1）Rt△AB1C1和Rt△AB2C2有什么关系?
Rt△AB1C1∽Rt△AB2C2
（3）如果改变B2在梯子上的位置（如B3C3 ）呢？由此你能得出什么结论？
Rt△AB1C1∽Rt△AB2C2∽ Rt△AB3C3
如图，在Rt△ABC中，如果锐角A确定，那么∠A的对边与邻边的比便随之确定，这个比叫做∠A的正切，记作tanA ，即
当锐角A变化时，tanA的值也随之变化.
梯子的倾斜程度与tanA有关系吗？
tanA的值越大，梯子越陡.
例1 下图表示两个自动扶梯，哪一个自动扶梯比较陡?
∵tan α＞tan β, ∴甲梯更陡.
正切也经常用来描述山坡的坡度.
如图，有一山坡在水平方向上每前进100m就升高60m，那么山坡的坡度就是
1. 如图，△ABC是等腰三角形，你能根据图中所给数据求出tanC 吗？
解：由图可知，D为AC的中点，则DC=2.
2. 如图，某人从山脚下的点A走了200m后到达山顶的点B. 已知点B到山脚的垂直距离为55m，求山坡的坡度. (结果精确到0.001m)