数学选择性必修 第一册1.1 空间向量及其运算多媒体教学ppt课件

这是一份数学选择性必修 第一册1.1 空间向量及其运算多媒体教学ppt课件，共32页。PPT课件主要包含了学习目标，复习回顾，共线向量，BP三点共线，共面向量，BC共面，课堂小结等内容，欢迎下载使用。

1.经历向量及其运算由平面空间推广的过程，了解空间向量的概念；2.掌握空间向量的加法、减法、数乘运算及其表示；3.掌握空间向量加法、减法、数乘的运算律；4.借助向量的线性运算的学习，提升数学运算素养.
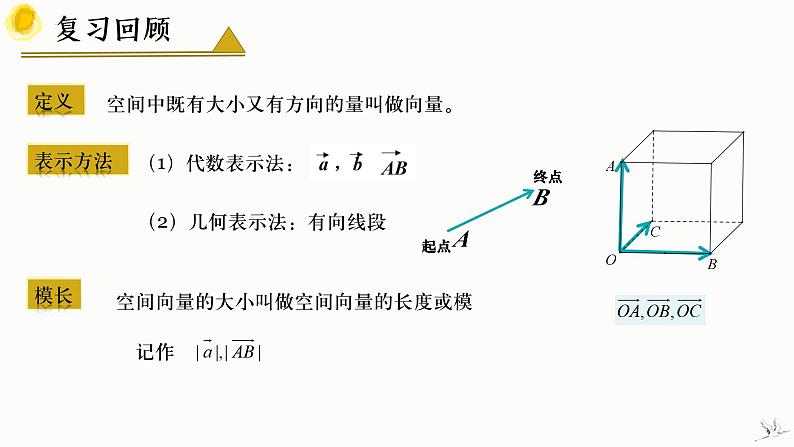
空间中既有大小又有方向的量叫做向量。
（2）几何表示法：有向线段
空间向量的大小叫做空间向量的长度或模
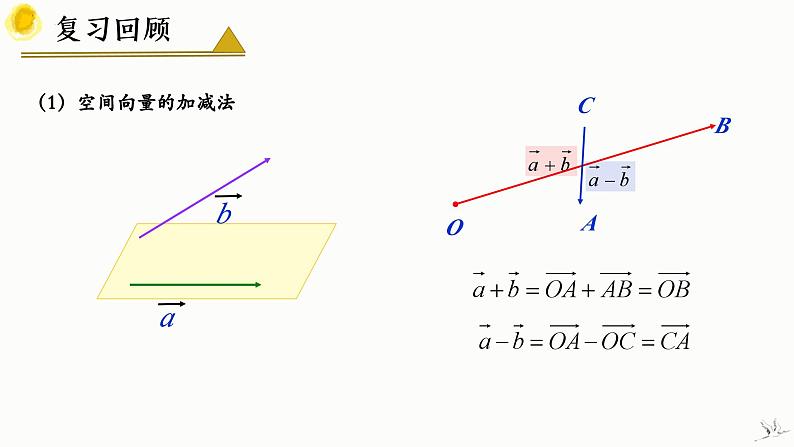
（1）空间向量的加减法
(2)实数与向量的积与平面向量一样，实数λ与空间向量a的乘积λa仍然是一个向量，称为向量的数乘运算，记作λa，其长度和方向规定如下：①|λa|＝____.②当λ>0时，λa与向量a方向相同；当λ<0时，λa与向量a方向 ；当λ＝0时，λa＝0.(3)空间向量数乘运算满足以下运算律①λ(μa)＝______； ②λ(a＋b)＝________；③(λ1＋λ2)a＝_________.
探究：对任意两个空间向量a,b,如果a＝λb（λ∈R），a与b有什么位置关系？反过来，a与b有什么位置关系时，a＝λb?
类似于平面向量共线的充要条件，对任意两个空间向量a，b（b≠0），a∥b的充要条件是存在实数λ，使a＝λb
（1）共线向量：如果表示空间向量的有向线段所在直线互相平行或重合,则这些向量叫做共线向量(或平行向量), 记作
由 知存在唯一的t, 满足
若在l上取 则有
①和②都称为空间直线的向量表示式，空间任意直线由空间一点及直线的方向向量唯一决定.
若点P是直线l上任意一点，则
反思感悟　向量共线的判定及应用(1)判断或证明两向量a，b(b≠0)共线，就是寻找实数λ，使a＝λb成立，为此常结合题目图形，运用空间向量的线性运算法则将目标向量化简或用同一组向量表达.(2)判断或证明空间中的三点(如P，A，B)共线的方法：是否存在实数λ，
1.共面向量:平行于同一平面的向量,叫做共面向量.
思考：空间任意两个向量是共面向量，则空间任意三个向量是否共面？
不一定，如图所示，空间中的三个向量不共面.
探究1：如果空间向量p与两个不共线向量a，b共面，那么可将三个向量平移到一个平面内，则有p＝xa＋yb
探究2：对空间两个不共线向量a，b共面，有p＝xa＋yb ， 那么向量p与向量a，b有什么位置关系？
∵xa，yb分别与a，b共线
∴xa，yb都在a，b确定的平面内， 且平行四边形也在a，b确定的平面内
∴p=xa+yb在a，b确定的平面内。
三个向量共面的充要条件：向量p与不共线向量a，b共面的充要条件是存在_____的有序实数对(x，y)__________
1.(多选)对空间任一点O和不共线的三点A，B，C，能得到P，A，B，C四点共面的是（ ）
3.(多选)下列条件中，使M与A，B，C一定共面的是（ ）
解析　A选项中，3－1－1＝1，四点共面，
∴点M，A，B，C共面.
且M，A，B，C四点共面，
5. 如图,已知平行四边形ABCD,从平面AC外一点O作射线OA，OB，OC，OD，在四条射线上分别取点E，F，G，H，使
证明：四点E，F，G，H共面
四点共面→有公共起点的三个向量共面
尝试用空间向量解决立体几何问题
方法总结选择恰当的向量表示问题中的几何元素通过向量运算得出几何元素的关系把运算结果“翻译”成相应的几何意义