山东省东营市2023年各地区中考考数学模拟（二模）试题按题型难易度分层分类汇编-01选择题（提升题）

这是一份山东省东营市2023年各地区中考考数学模拟（二模）试题按题型难易度分层分类汇编-01选择题（提升题），共13页。
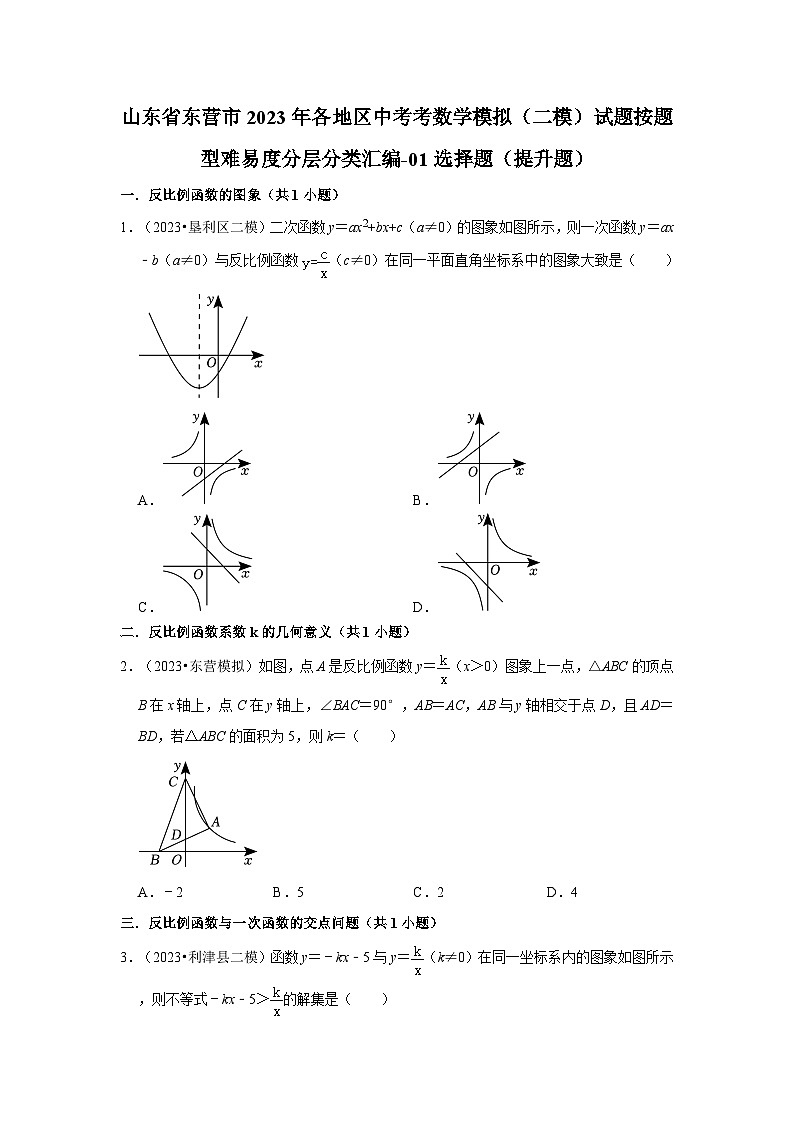
山东省东营市2023年各地区中考考数学模拟（二模）试题按题型难易度分层分类汇编-01选择题（提升题）一．反比例函数的图象（共1小题）1．（2023•垦利区二模）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，则一次函数y＝ax﹣b（a≠0）与反比例函数（c≠0）在同一平面直角坐标系中的图象大致是（　　）A． B． C． D．二．反比例函数系数k的几何意义（共1小题）2．（2023•东营模拟）如图，点A是反比例函数y＝（x＞0）图象上一点，△ABC的顶点B在x轴上，点C在y轴上，∠BAC＝90°，AB＝AC，AB与y轴相交于点D，且AD＝BD，若△ABC的面积为5，则k＝（　　）A．﹣2 B．5 C．2 D．4三．反比例函数与一次函数的交点问题（共1小题）3．（2023•利津县二模）函数y＝﹣kx﹣5与y＝（k≠0）在同一坐标系内的图象如图所示，则不等式﹣kx﹣5＞的解集是（　　）A．x＜0 B．x＞0 C．x≠0 D．x＜1四．平行线的性质（共1小题）4．（2023•东营模拟）把一块直尺与一块含30°的直角三角板如图放置，若∠1＝34°，则∠2的度数为（　　）A．114° B．124° C．116° D．126°五．四边形综合题（共1小题）5．（2023•广饶县二模）如图，正方形ABCD中，AB＝6，点E在边CD上，且CE＝2DE．将△ADE沿AE对折至△AFE，延长EF交BC于点G，连结AG、BF、CF．下列结论：①△ABG≌△AFG；②FG＝CG；③AG∥CF；④S△BFC＝．其中正确结论的个数是（　　）A．1个 B．2个 C．3个 D．4个六．翻折变换（折叠问题）（共1小题）6．（2023•利津县二模）如图，已知△ABC，AB＝AC，BC＝16，AD⊥BC，∠ABC的平分线交AD于点E，且DE＝4．将∠C沿GM折叠，使点C与点恰好重合，下列结论：①DM＝4，②点E到AC的距离为3，③EM＝5，④四边形CGEM是菱形．其中正确的个数是（　　）A．1 B．2 C．3 D．4七．坐标与图形变化-旋转（共1小题）7．（2023•利津县二模）如图，在平面直角坐标系中，△ABC的顶点都在方格线的格点上，将△ABC绕点A逆时针方向旋转90°，得到△A'B'C'，则点C的对应点C'的坐标为（　　）A．（2，﹣3） B．（﹣2，3） C．（﹣2，2） D．（﹣3，2）八．相似三角形的判定与性质（共1小题）8．（2023•东营模拟）在四边形ABCD中，AD∥BC，∠ABC＝90°，AB＝BC，E为AB边上一点，∠BCE＝15°，且AE＝A D．连接DE交对角线AC于H，连接BH．下列结论正确的是（　　）①AC⊥DE；②；③CD＝2DH；④．A．①②④ B．①②③ C．①③④ D．①②③④
山东省东营市2023年各地区中考考数学模拟（二模）试题按题型难易度分层分类汇编-01选择题（提升题）参考答案与试题解析一．反比例函数的图象（共1小题）1．（2023•垦利区二模）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，则一次函数y＝ax﹣b（a≠0）与反比例函数（c≠0）在同一平面直角坐标系中的图象大致是（　　）A． B． C． D．【答案】A【解答】解：∵二次函数的图象开口向上，与y轴的交点在y轴负半轴，∴a＞0，c＜0，由图可得对称轴为直线y＝﹣，﹣＜0，∴b＞0，∴一次函数y＝ax﹣b的图象经过一，三，四象限，的图象在二，四象限，∴B，C，D不符合题意，A符合题意；故选：A．二．反比例函数系数k的几何意义（共1小题）2．（2023•东营模拟）如图，点A是反比例函数y＝（x＞0）图象上一点，△ABC的顶点B在x轴上，点C在y轴上，∠BAC＝90°，AB＝AC，AB与y轴相交于点D，且AD＝BD，若△ABC的面积为5，则k＝（　　）A．﹣2 B．5 C．2 D．4【答案】C【解答】解：作AE⊥y轴于E，AF⊥x轴于F，则AE∥x轴，∴∠EAB＝∠ABF，∵∠BAC＝90°，∴∠CAE+∠EAB＝90°，∴∠CAE+∠ABF＝90°，∵∠ABF+∠BAF＝90°，∴∠BAF＝∠CAE，∵AB＝AC，∠AFB＝∠AEC＝90°，∴△ABF≌△ACE（AAS），∴AE＝AF，BF＝CE，设A（m，m），∵AD＝BD，AF∥y轴，∴BO＝FO，∴B（﹣m，0），∴CE＝BF＝2m，∴AB2＝AF2+BF2＝m2+（2m）2＝5m2，∵△ABC的面积为5，∴AB•AC＝AB2＝5，∴×5m2＝5，∴m2＝2，∵点A是反比例函数y＝（x＞0）图象上一点，∴k＝m•m＝m2＝2，故选：C．三．反比例函数与一次函数的交点问题（共1小题）3．（2023•利津县二模）函数y＝﹣kx﹣5与y＝（k≠0）在同一坐标系内的图象如图所示，则不等式﹣kx﹣5＞的解集是（　　）A．x＜0 B．x＞0 C．x≠0 D．x＜1【答案】B【解答】解：不等式﹣kx﹣5＞的解集是：x＞0．故选：B．四．平行线的性质（共1小题）4．（2023•东营模拟）把一块直尺与一块含30°的直角三角板如图放置，若∠1＝34°，则∠2的度数为（　　）A．114° B．124° C．116° D．126°【答案】B【解答】解：如图，∵a∥b，∴∠2＝∠3，∵∠3＝∠1+90°，∠1＝34°，∴∠3＝124°，∴∠2＝∠3＝124°，故选：B．五．四边形综合题（共1小题）5．（2023•广饶县二模）如图，正方形ABCD中，AB＝6，点E在边CD上，且CE＝2DE．将△ADE沿AE对折至△AFE，延长EF交BC于点G，连结AG、BF、CF．下列结论：①△ABG≌△AFG；②FG＝CG；③AG∥CF；④S△BFC＝．其中正确结论的个数是（　　）A．1个 B．2个 C．3个 D．4个【答案】D【解答】解：∵正方形ABCD的边长为6，CE＝2DE，∴DE＝2，EC＝4，∵把△ADE沿AE折叠使△ADE落在△AFE的位置，∴AF＝AD＝6，EF＝ED＝2，∠AFE＝∠D＝90°，∠FAE＝∠DAE，在Rt△ABG和Rt△AFG中，，∴Rt△ABG≌Rt△AFG（HL），∴GB＝GF，∠BAG＝∠FAG，∴∠GAE＝∠FAE+∠FAG＝∠BAD＝45°，故①正确；设BG＝x，则GF＝x，CG＝BC﹣BG＝6﹣x，在Rt△CGE中，GE＝x+2，EC＝4，CG＝6﹣x，∵CG2+CE2＝GE2，∴（6﹣x）2+42＝（x+2）2，解得x＝3，∴BG＝3，CG＝6﹣3＝3∴BG＝CG＝FG，故②正确；∵GF＝GC，∴∠GFC＝∠GCF，又∵Rt△ABG≌Rt△AFG，∴∠AGB＝∠AGF，而∠BGF＝∠GFC+∠GCF，∴∠AGB+∠AGF＝∠GFC+∠GCF，∴∠AGB＝∠GCF，∴CF∥AG，故③正确；过F作FH⊥DC于H，∵BC⊥DH，∴FH∥GC，∴△EFH∽△EGC，∴，∵EF＝DE＝2，GF＝3，∴EG＝5，∴＝，∴FH＝GC＝×3＝，∴S△FGC＝S△GCE﹣S△FEC＝×3×4﹣×4×＝，∵BG＝GC，∴S△BFC＝2S△FGC＝，故④正确．故选：D．六．翻折变换（折叠问题）（共1小题）6．（2023•利津县二模）如图，已知△ABC，AB＝AC，BC＝16，AD⊥BC，∠ABC的平分线交AD于点E，且DE＝4．将∠C沿GM折叠，使点C与点恰好重合，下列结论：①DM＝4，②点E到AC的距离为3，③EM＝5，④四边形CGEM是菱形．其中正确的个数是（　　）A．1 B．2 C．3 D．4【答案】B【解答】解：在△ABC中，AB＝AC，BC＝16，AD⊥BC，∴BD＝DC＝BC＝8，如图，过点E作EF⊥AB于点F，EH⊥AC于点H，∵AD⊥BC，AB＝AC，∴AE平分∠BAC，∴EH＝EF，∵BE是∠ABD的角平分线，∵ED⊥BC，EF⊥AB，∴EF＝ED，∴EH＝ED＝4，故②错误；由折叠性质可得：EM＝MC，DM+MC＝DM+EM＝CD＝8，设DM＝x，则EM＝8﹣x，Rt△EDM中，EM2＝DM2+DE2，∴（8﹣x）2＝42+x2，解得：x＝3，∴EM＝MC＝5，故③正确；∴DM＝DC﹣CM＝3，故①错误；连接CE，由内心可知CE平分∠ACD，∴∠GCE＝∠ECD，由折叠可知CM＝EM，∴∠MEC＝∠ECM，∴∠MEC＝∠GCE，∴EM∥AC，∴∠EMG＝∠CGM，∴∠CGM＝∠CMG，∴CM＝CG，∴EM＝CM＝CG＝EG，∴四边形CGEM是菱形；故④正确，故选：B．七．坐标与图形变化-旋转（共1小题）7．（2023•利津县二模）如图，在平面直角坐标系中，△ABC的顶点都在方格线的格点上，将△ABC绕点A逆时针方向旋转90°，得到△A'B'C'，则点C的对应点C'的坐标为（　　）A．（2，﹣3） B．（﹣2，3） C．（﹣2，2） D．（﹣3，2）【答案】B【解答】解：如图，△AB′C′即为所求，C′（﹣2，3）．故选：B．八．相似三角形的判定与性质（共1小题）8．（2023•东营模拟）在四边形ABCD中，AD∥BC，∠ABC＝90°，AB＝BC，E为AB边上一点，∠BCE＝15°，且AE＝A D．连接DE交对角线AC于H，连接BH．下列结论正确的是（　　）①AC⊥DE；②；③CD＝2DH；④．A．①②④ B．①②③ C．①③④ D．①②③④【答案】C【解答】解：∵AD∥BC，∠ABC＝90°，∴∠BAD＝90°，又∵AB＝BC，∴∠BAC＝45°，∴∠CAD＝∠BAD﹣∠BAC＝90°﹣45°＝45°，∴∠BAC＝∠CAD，∴AH⊥ED，即AC⊥ED，故①正确；∵△CHE为直角三角形，且∠HEC＝60°，∴EC＝2EH，∵∠ECB＝15°，∴EC≠4EB，∴EH≠2EB；故②错误．由①知，∠BAC＝∠CAD，在△ACD和△ACE中，，∴△ACD≌△ACE（SAS），∴CD＝CE，∵∠BCE＝15°，∴∠BEC＝90°﹣∠BCE＝90°﹣15°＝75°，∴∠CED＝180°﹣∠BEC﹣∠AED＝180°﹣75°﹣45°＝60°，∴△CDE为等边三角形，∴∠DCH＝30°，∴CD＝2DH，故③正确；过H作HM⊥AB于M，∴HM∥BC，∴△AMH∽△ABC，∴，∵∠DAC＝∠ADH＝45°，∴DH＝AH，∴，∵△BEH和△CBE有公共底BE，∴，故④正确，∴结论正确的为①③④．故选：C．