辽宁省盘锦市2021-2023三年中考数学真题分类汇编-02填空题知识点分类

这是一份辽宁省盘锦市2021-2023三年中考数学真题分类汇编-02填空题知识点分类，共20页。试卷主要包含了计算，分解因式等内容，欢迎下载使用。

辽宁省盘锦市2021-2023三年中考数学真题分类汇编-02填空题知识点分类
一．科学记数法—表示较大的数（共2小题）
1．（2022•盘锦）目前，我国基本医疗保险覆盖已超过13.5亿人，数据13.5亿用科学记数法表示为 　 　．
2．（2021•盘锦）建党100周年期间，我市人社系统不断提升服务能力和水平，让我市约1300000参保人员获得更高质量的社会保障福祉，数据1300000用科学记数法表示为 　 　．
二．实数的性质（共1小题）
3．（2021•盘锦）计算：|﹣2|+＝　 　．
三．提公因式法与公式法的综合运用（共3小题）
4．（2022•盘锦）分解因式：x2y﹣2xy2+y3＝　 　．
5．（2021•盘锦）分解因式：2m2﹣2＝　 　．
6．（2023•盘锦）分解因式：4a2b﹣b＝　 　．
四．二次根式的加减法（共1小题）
7．（2023•盘锦）计算：﹣＝　 　．
五．由实际问题抽象出二元一次方程组（共1小题）
8．（2023•盘锦）我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设有x只鸡，y只兔，根据题意，可列方程组为 　 　．
六．解一元一次不等式（共1小题）
9．（2023•盘锦）不等式≥的解集是 　 　．
七．一次函数图象与系数的关系（共1小题）
10．（2023•盘锦）关于x的一次函数y＝（2a+1）x+a﹣2，若y随x的增大而增大，且图象与y轴的交点在原点下方，则实数a的取值范围是 　 　．
八．一次函数图象上点的坐标特征（共1小题）
11．（2022•盘锦）点A（x1，y1），B（x2，y2）在一次函数y＝（a﹣2）x+1的图象上，当x1＞x2时，y1＜y2，则a的取值范围是 　 　．
九．圆周角定理（共1小题）
12．（2021•盘锦）如图，在平面直角坐标系xOy中，点A在x轴负半轴上，点B在y轴正半轴上，⊙D经过A，B，O，C四点，∠ACO＝120°，AB＝4，则圆心点D的坐标是 　 　．

一十．弧长的计算（共1小题）
13．（2022•盘锦）如图，在△ABC中，AB＝AC，∠A＝50°，以AB为直径的⊙O交边BC，AC于D，E两点，AC＝2，则的长是 　 　．

一十一．扇形面积的计算（共1小题）
14．（2021•盘锦）如图，⊙A，⊙B，⊙C两两不相交，且半径都等于2，则图中三个扇形（即阴影部分）的面积之和为 　 　．（结果保留π）

一十二．作图—基本作图（共1小题）
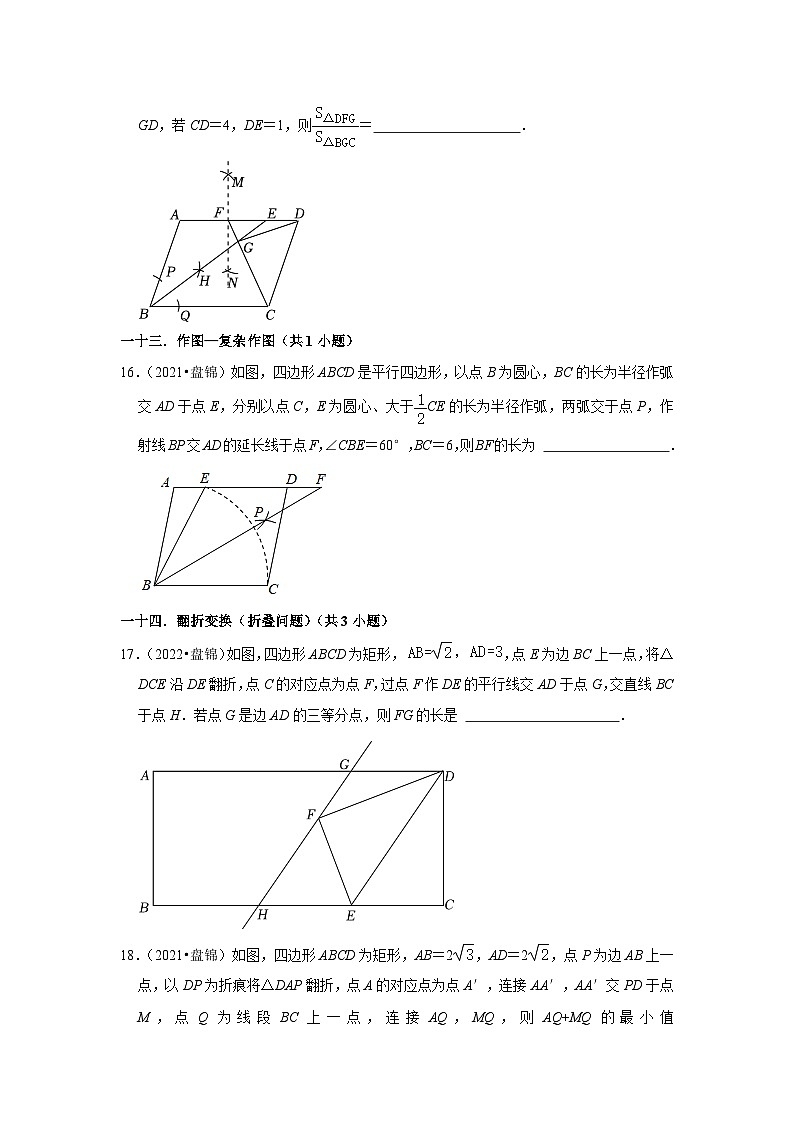
15．（2023•盘锦）如图，四边形ABCD是平行四边形，以点B为圆心，任意长为半径画弧分别交AB和BC于点P，Q，以点P，Q为圆心，大于PQ的长为半径画弧，两弧交于点H，作射线BH交边AD于点E；分别以点A，E为圆心，大于AE的长为半径画弧，两弧相交于M，N两点，作直线MN交边AD于点F，连接CF，交BE于点G，连接GD，若CD＝4，DE＝1，则＝　 　．

一十三．作图—复杂作图（共1小题）
16．（2021•盘锦）如图，四边形ABCD是平行四边形，以点B为圆心，BC的长为半径作弧交AD于点E，分别以点C，E为圆心、大于CE的长为半径作弧，两弧交于点P，作射线BP交AD的延长线于点F，∠CBE＝60°，BC＝6，则BF的长为 　 　．

一十四．翻折变换（折叠问题）（共3小题）
17．（2022•盘锦）如图，四边形ABCD为矩形，，点E为边BC上一点，将△DCE沿DE翻折，点C的对应点为点F，过点F作DE的平行线交AD于点G，交直线BC于点H．若点G是边AD的三等分点，则FG的长是 　 　．

18．（2021•盘锦）如图，四边形ABCD为矩形，AB＝2，AD＝2，点P为边AB上一点，以DP为折痕将△DAP翻折，点A的对应点为点A′，连接AA′，AA′交PD于点M，点Q为线段BC上一点，连接AQ，MQ，则AQ+MQ的最小值是 　 　．

19．（2023•盘锦）如图，四边形ABCD是矩形，AB＝，BC＝6，点E为边BC的中点，点F为边AD上一点，将四边形ABEF沿EF折叠，点A的对应点为点A′，点B的对应点为点B′，过点B′作B′H⊥BC于点H，若B′H＝2，则FD的长是 　 　．

一十五．旋转的性质（共1小题）
20．（2022•盘锦）如图，在△ABC中，AB＝AC，∠ABC＝30°，点D为BC的中点，将△ABC绕点D逆时针旋转得到△A'B'C'，当点A的对应点A'落在边AB上时，点C'在BA的延长线上，连接BB'，若AA'＝1，则△BB'D的面积是 　 　．

一十六．位似变换（共1小题）
21．（2023•盘锦）如图，△ABO的顶点坐标是A（2，6），B（3，1），O（0，0），以点O为位似中心，将△ABO缩小为原来的，得到△A′B′O，则点A′的坐标为 　 　．

一十七．折线统计图（共1小题）
22．（2022•盘锦）如图是根据甲、乙两城市一周的日均气温绘制的折线统计图，根据统计图判断本周的日平均气温较稳定的城市是 　 　．（选填“甲”或“乙”）

一十八．概率公式（共2小题）
23．（2022•盘锦）若关于x的方程x2﹣3x+m＝0有两个不相等的实数根，且m≥﹣3，则从满足条件的所有整数m中随机选取一个，恰好是负数的概率是 　 　．
24．（2021•盘锦）从不等式组的所有整数解中任取一个数，它是偶数的概率是 　 　．

辽宁省盘锦市2021-2023三年中考数学真题分类汇编-02填空题知识点分类
参考答案与试题解析
一．科学记数法—表示较大的数（共2小题）
1．（2022•盘锦）目前，我国基本医疗保险覆盖已超过13.5亿人，数据13.5亿用科学记数法表示为 　1.35×109　．
【答案】1.35×109．
【解答】解：13.5亿＝1350000000＝1.35×109．
故答案为：1.35×109．
2．（2021•盘锦）建党100周年期间，我市人社系统不断提升服务能力和水平，让我市约1300000参保人员获得更高质量的社会保障福祉，数据1300000用科学记数法表示为 　1.3×106　．
【答案】1.3×106．
【解答】解：数据1300000用科学记数法表示为1.3×106．
故答案为：1.3×106．
二．实数的性质（共1小题）
3．（2021•盘锦）计算：|﹣2|+＝　2+　．
【答案】2+．
【解答】解：原式＝2﹣+2
＝2+．
故答案为：2+．
三．提公因式法与公式法的综合运用（共3小题）
4．（2022•盘锦）分解因式：x2y﹣2xy2+y3＝　y（x﹣y）2　．
【答案】见试题解答内容
【解答】解：∵x2y﹣2xy2+y3＝y（x2﹣2xy+y2）＝y（x﹣y）2．
故答案为：y（x﹣y）2．
5．（2021•盘锦）分解因式：2m2﹣2＝　2（m+1）（m﹣1）　．
【答案】见试题解答内容
【解答】解：2m2﹣2＝2（m2﹣1）＝2（m+1）（m﹣1）．
故答案为：2（m+1）（m﹣1）．
6．（2023•盘锦）分解因式：4a2b﹣b＝　b（2a+1）（2a﹣1）　．
【答案】见试题解答内容
【解答】解：原式＝b（4a2﹣1）＝b（2a+1）（2a﹣1），
故答案为：b（2a+1）（2a﹣1）
四．二次根式的加减法（共1小题）
7．（2023•盘锦）计算：﹣＝　1　．
【答案】1．
【解答】解：﹣＝3﹣2＝1．
故答案为：1．
五．由实际问题抽象出二元一次方程组（共1小题）
8．（2023•盘锦）我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设有x只鸡，y只兔，根据题意，可列方程组为 　　．
【答案】．
【解答】解：由题意可得，．
故答案为：．
六．解一元一次不等式（共1小题）
9．（2023•盘锦）不等式≥的解集是 　x≥﹣3　．
【答案】x≥﹣3．
【解答】解：去分母得，3（x+1）≥2x，
去括号得，3x+3≥2x，
移项合并同类项得，x≥﹣3．
故答案为：x≥﹣3．
七．一次函数图象与系数的关系（共1小题）
10．（2023•盘锦）关于x的一次函数y＝（2a+1）x+a﹣2，若y随x的增大而增大，且图象与y轴的交点在原点下方，则实数a的取值范围是 　﹣＜a＜2　．
【答案】﹣＜a＜2．
【解答】解：根据题意得，
解得：﹣＜a＜2．
故答案为：﹣＜a＜2．
八．一次函数图象上点的坐标特征（共1小题）
11．（2022•盘锦）点A（x1，y1），B（x2，y2）在一次函数y＝（a﹣2）x+1的图象上，当x1＞x2时，y1＜y2，则a的取值范围是 　a＜2　．
【答案】a＜2．
【解答】解：∵当x1＞x2时，y1＜y2，
∴a﹣2＜0，
∴a＜2，
故答案为：a＜2．
九．圆周角定理（共1小题）
12．（2021•盘锦）如图，在平面直角坐标系xOy中，点A在x轴负半轴上，点B在y轴正半轴上，⊙D经过A，B，O，C四点，∠ACO＝120°，AB＝4，则圆心点D的坐标是 　（﹣，1）　．

【答案】（﹣，1）．
【解答】解：∵四边形ABOC为圆的内接四边形，
∴∠ABO+∠ACO＝180°，
∴∠ABO＝180°﹣120°＝60°，
∵∠AOB＝90°，
∴AB为⊙D的直径，
∴D点为AB的中点，
在Rt△ABO中，∵∠ABO＝60°，
∴OB＝AB＝2，
∴OA＝OB＝2，
∴A（﹣2，0），B（0，2），
∴D点坐标为（﹣，1）．
故答案为（﹣，1）．
一十．弧长的计算（共1小题）
13．（2022•盘锦）如图，在△ABC中，AB＝AC，∠A＝50°，以AB为直径的⊙O交边BC，AC于D，E两点，AC＝2，则的长是 　　．

【答案】．
【解答】解：连接OE，OD，
∵AB＝AC，∠A＝50°，
∴∠B＝∠C＝＝65°，
又∵OB＝OD，OA＝OE，
∴∠B＝∠ODB＝65°，∠A＝∠OEA＝50°，
∴∠BOD＝50°，∠AOE＝80°，
∴∠DOE＝50°，
由于半径为1，
∴的长是＝．
故答案为：．

一十一．扇形面积的计算（共1小题）
14．（2021•盘锦）如图，⊙A，⊙B，⊙C两两不相交，且半径都等于2，则图中三个扇形（即阴影部分）的面积之和为 　2π　．（结果保留π）

【答案】2π．
【解答】解：∵三个扇形的半径都是2，三个圆心角的和是180°，
∴图中的三个扇形（即三个阴影部分）的面积之和为＝2π．
故答案为：2π．
一十二．作图—基本作图（共1小题）
15．（2023•盘锦）如图，四边形ABCD是平行四边形，以点B为圆心，任意长为半径画弧分别交AB和BC于点P，Q，以点P，Q为圆心，大于PQ的长为半径画弧，两弧交于点H，作射线BH交边AD于点E；分别以点A，E为圆心，大于AE的长为半径画弧，两弧相交于M，N两点，作直线MN交边AD于点F，连接CF，交BE于点G，连接GD，若CD＝4，DE＝1，则＝　　．

【答案】．
【解答】解：由作图得：BE平分∠ABC，MN垂直平分AE，
∴∠ABE＝∠EBC，AF＝EF，
在▱ABCD中，AD∥BC，AD＝BC，AB＝CD＝4，
∴∠AEB＝∠EBC，
∴∠AEB＝∠ABE，
∴AE＝AB＝CD＝4，
∴AF＝EF＝2，
∴FD＝3DE，BC＝AD＝5，
S△DEG＝x，则S△EFG＝2x，S△FDG＝3x，
∵AD∥BC，
∴△EFG∽△BCG，
∴＝（）2＝（）2＝，
S△BCG＝12.5x，
∴＝＝，
故答案为：．
一十三．作图—复杂作图（共1小题）
16．（2021•盘锦）如图，四边形ABCD是平行四边形，以点B为圆心，BC的长为半径作弧交AD于点E，分别以点C，E为圆心、大于CE的长为半径作弧，两弧交于点P，作射线BP交AD的延长线于点F，∠CBE＝60°，BC＝6，则BF的长为 　6　．

【答案】6．
【解答】解：由作法得BE＝BC＝6，BF平分∠CBE，
∴∠CBF＝∠EBF＝∠CBE＝30°，
∵四边形ABCD为平行四边形，
∴AD∥BC，
∴∠F＝∠CBF，
∴∠F＝∠EBF＝30°，
∴BE＝FE，
过E点作EH⊥BF于H，如图，则BH＝FH，
在Rt△BEH中，∵EH＝BE＝3，
∴BH＝EH＝3，
∴BF＝2BH＝6．
故答案为6．

一十四．翻折变换（折叠问题）（共3小题）
17．（2022•盘锦）如图，四边形ABCD为矩形，，点E为边BC上一点，将△DCE沿DE翻折，点C的对应点为点F，过点F作DE的平行线交AD于点G，交直线BC于点H．若点G是边AD的三等分点，则FG的长是 　或　．

【答案】或．
【解答】解：①如图，过点E作EM⊥GH于点M，

∵DE∥GH，AD∥BC，
∴四边形HEDG是平行四边形，
∴，
∵折叠，
∴∠FED＝∠CED，
∵∠MED＝90°，
即∠FEM+∠FED＝90°，
∴∠CED+∠HEM＝90°，
∴∠HEM＝∠FEM，
∵∠EMF＝∠EMH＝90°，ME＝ME，
∴△HEM≌△FEM（ASA），
∴HM＝MF，EF＝HE＝1，
∴EF＝EC＝1，
∵四边形ABCD是矩形，
∴，
Rt△EDC中，，
∴，
∵ME⊥HG，HG∥DE，
∴，
∴，
Rt△HME中，，
∴，
②如图，当时，


同理可得HE＝GD＝AD﹣AG＝3﹣1＝2，EC＝EF＝HE＝2，
∴，
∴，
Rt△HME中，，
∴，
故答案为：或．
18．（2021•盘锦）如图，四边形ABCD为矩形，AB＝2，AD＝2，点P为边AB上一点，以DP为折痕将△DAP翻折，点A的对应点为点A′，连接AA′，AA′交PD于点M，点Q为线段BC上一点，连接AQ，MQ，则AQ+MQ的最小值是 　4　．

【答案】4．
【解答】解：如图，作点A关于BC的对称点T，取AD的中点R，连接BT，QT，RT，RM，MT．

∵四边形ABCD是矩形，
∴∠RAT＝90°，
∵AR＝DR＝，AT＝2AB＝4，
∴RT＝＝＝5，
∵A，A′关于DP对称，
∴AA′⊥DP，
∴∠AMD＝90°，
∵AR＝RD，
∴RM＝AD＝，
∵MT≥RT﹣RM，
∴MT≥4，
∴MT的最小值为4，
∵QA+QM＝QT+QM≥MT，
∴QA+QM≥4
∴QA+QM的最小值为4．
故答案为：4．
19．（2023•盘锦）如图，四边形ABCD是矩形，AB＝，BC＝6，点E为边BC的中点，点F为边AD上一点，将四边形ABEF沿EF折叠，点A的对应点为点A′，点B的对应点为点B′，过点B′作B′H⊥BC于点H，若B′H＝2，则FD的长是 　　．

【答案】．
【解答】解：如图，设B′E交AD于点G，过点E作EM⊥AD于点M，

则∠AME＝90°，
∵点E为边BC的中点，
∴BE＝CE＝BC＝3，
∵四边形ABCD为矩形，BC＝6，
∴AD＝BC＝6，∠A＝∠B＝90°，AD∥BC，
∴∠AME＝∠A＝∠B＝90°，
∴四边形ABEM为矩形，
∴AB＝ME＝，AM＝BE＝3，
由折叠可知，BE＝B′E＝3，∠BEF＝∠B′EF，
∵AD∥BC，
∴∠GFE＝∠BEF，
∴∠GFE＝∠B′EF，即∠GFE＝∠GEF，
∴FG＝EG，
∵B′H⊥BC，
∴∠B′HE＝90°，
在Rt△B′HE中，EH＝＝＝1，
∵ME⊥BC，B′H⊥BC，
∴∠EMG＝∠B′HE＝90°，
∵AD∥BC，
∴∠EGM＝∠B′EH，
∴△EMG∽△B′HE，
∴，即＝，
∴EG＝＝FG，MG＝，
∴FM＝FG﹣MG＝＝，
∴AF＝AM﹣FM＝，
∴FD＝AD﹣AF＝6﹣（3﹣）＝．
故答案为：．
一十五．旋转的性质（共1小题）
20．（2022•盘锦）如图，在△ABC中，AB＝AC，∠ABC＝30°，点D为BC的中点，将△ABC绕点D逆时针旋转得到△A'B'C'，当点A的对应点A'落在边AB上时，点C'在BA的延长线上，连接BB'，若AA'＝1，则△BB'D的面积是 　　．

【答案】．
【解答】解：如图所示，设A'B'与BD交于点O，连接A'D和AD，


∵点D为BC的中点，AB＝AC，∠ABC＝30°，
∴AD⊥BC，A'D⊥B'C'，A'D是∠B′A′C′的角平分线，AD是∠BAC的角平分线，
∴∠B'A'C'＝120°，∠BAC＝120°，
∴∠BAD＝∠B'A'D＝60°，
∵A'D＝AD，
∴△A'AD是等边三角形，
∴A'A＝AD＝A'D＝1，
∵∠BA'B'＝180°﹣∠B'A'C'＝60°，
∴∠BA'B'＝∠A'AD，
∴A'B'∥AD，
∴A′O⊥BC，
∴，
∴，
∵A'B'＝2A'D＝2，
∵∠A'BD＝∠A'DO＝30°，
∴BO＝OD，
∴，，
∴．
一十六．位似变换（共1小题）
21．（2023•盘锦）如图，△ABO的顶点坐标是A（2，6），B（3，1），O（0，0），以点O为位似中心，将△ABO缩小为原来的，得到△A′B′O，则点A′的坐标为 　（，2）或（﹣，﹣2）　．

【答案】（，2）或（﹣，﹣2）．
【解答】解：∵以原点O为位似中心，把△ABC缩小为原来的，可以得到△A'B'O，点A的坐标为（2，6），
∴点A'的坐标是（2×，6×）或（2×（﹣），6×（﹣）），即（，2）或（﹣，﹣2）．
故答案为：（，2）或（﹣，﹣2）．
一十七．折线统计图（共1小题）
22．（2022•盘锦）如图是根据甲、乙两城市一周的日均气温绘制的折线统计图，根据统计图判断本周的日平均气温较稳定的城市是 　乙　．（选填“甲”或“乙”）

【答案】乙．
【解答】解：由图知，乙的气温波动较小，故本周的日平均气温稳定的是乙城市．
故答案为：乙．
一十八．概率公式（共2小题）
23．（2022•盘锦）若关于x的方程x2﹣3x+m＝0有两个不相等的实数根，且m≥﹣3，则从满足条件的所有整数m中随机选取一个，恰好是负数的概率是 　　．
【答案】．
【解答】解：根据题意，关于x的方程x2﹣3x+m＝0有两个不相等的实数根，
故该一元二次方程的根的判别式Δ＞0，即Δ＝（﹣3）2﹣4×1×m＞0，
解得，
又∵m≥﹣3，
∴，
∴满足条件的所有整数为﹣3、﹣2、﹣1、0、1、2共计6个，其中负数有﹣3、﹣2、﹣1共计3个，
∴满足条件的所有整数m中随机选取一个，恰好是负数的概率是．
故答案为：．
24．（2021•盘锦）从不等式组的所有整数解中任取一个数，它是偶数的概率是 　　．
【答案】．
【解答】解：∵，
由①得：x≥1，
由②得：x≤5，
∴不等式组的解集为：1≤x≤5，
∴整数解有：1，2，3，4，5；
∴它是偶数的概率是．
故答案为．