人教A版高中数学必修第一册第3章一元二次函数、方程和不等式习题课单调性与奇偶性的综合应用分层作业课件

这是一份人教A版高中数学必修第一册第3章一元二次函数、方程和不等式习题课单调性与奇偶性的综合应用分层作业课件，共16页。

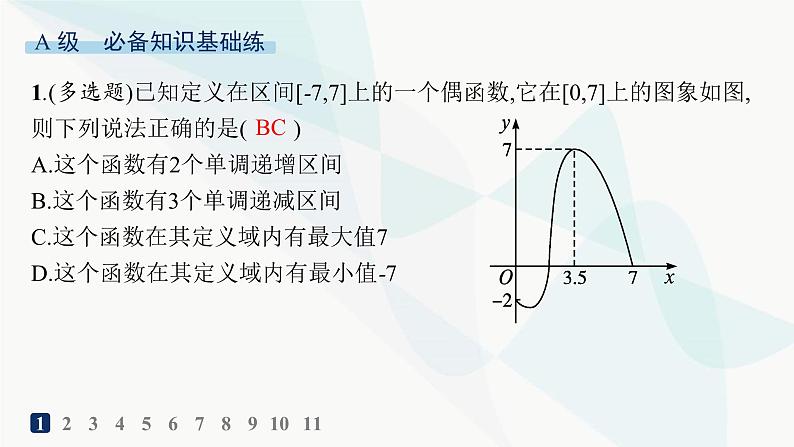
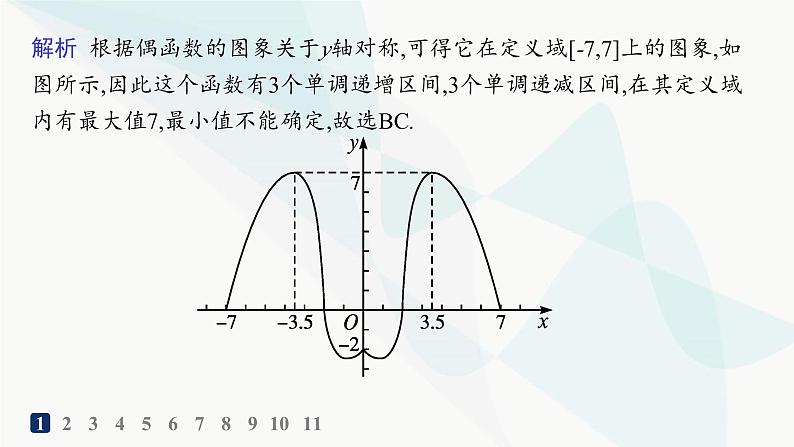
第三章习题课　单调性与奇偶性的综合应用12345678910111.(多选题)已知定义在区间[-7,7]上的一个偶函数,它在[0,7]上的图象如图,则下列说法正确的是(　　)A.这个函数有2个单调递增区间B.这个函数有3个单调递减区间C.这个函数在其定义域内有最大值7D.这个函数在其定义域内有最小值-7BC解析 根据偶函数的图象关于y轴对称,可得它在定义域[-7,7]上的图象,如图所示,因此这个函数有3个单调递增区间,3个单调递减区间,在其定义域内有最大值7,最小值不能确定,故选BC.123456789101112345678910112.下列函数是奇函数,且在(0,+∞)上为增函数的是(　　) D 12345678910113.偶函数y=f(x)在区间[0,4]上单调递减,则有(　　)A.f(-1)>f(2)>f(-3) B.f(2)>f(-1)>f(-3)C.f(-3)>f(-1)>f(2) D.f(-1)>f(-3)>f(2)A 解析 由y=f(x)为偶函数,则f(-1)=f(1),f(-3)=f(3),又因为函数y=f(x)在区间[0,4]上单调递减,所以f(1)>f(2)>f(3),即f(-1)>f(2)>f(-3),故选A.12345678910114.若奇函数f(x)在区间[-2,-1]上单调递减,则函数f(x)在区间[1,2]上(　　)A.单调递增,且有最小值为f(1)B.单调递增,且有最大值为f(1)C.单调递减,且有最小值为f(2)D.单调递减,且有最大值为f(2)C解析 根据奇函数的图象关于原点对称,所以其在y轴两侧单调性相同,因为f(x)在区间[-2,-1]上单调递减,所以f(x)在区间[1,2]上单调递减,所以f(x)在区间[1,2]上有最大值f(1),最小值f(2),故选C.1234567891011B解析 ∵函数f(x)=(m-1)x2+2mx+3是R上的偶函数,∴f(-x)=(m-1)x2-2mx+3=f(x)=(m-1)x2+2mx+3,∴m=0,即f(x)=-x2+3.∴f(x)在(-∞,0)上单调递增,123456789101112345678910116.f(x)是定义在[-6,6]上的偶函数,且f(3)>f(1),则下列各式一定成立的是(　　)A.f(0)f(2)C.f(-1)f(0)C解析 ∵f(x)是偶函数,∴f(1)=f(-1),又f(3)>f(1),故f(3)>f(-1).故选C.12345678910117.[2023安徽宿州高一月考]已知奇函数f(x)在定义域R上是增函数,则不等式f(4x-3x2)+f(7)>0的解集是　　　　　　　. 解析 ∵f(4x-3x2)+f(7)>0,∴f(4x-3x2)>-f(7).又f(x)为定义域R上的奇函数,∴f(4x-3x2)>f(-7).12345678910118.已知函数f(x)的定义域为(-1,1),且满足下列条件:①f(x)为奇函数;②f(x)在定义域上是减函数.若f(1-a)+f(1-a2)<0,求实数a的取值范围.解 ∵f(x)为奇函数,∴f(1-a2)=-f(a2-1),∴f(1-a)+f(1-a2)<0,则f(1-a)<-f(1-a2),即f(1-a)0,故y=f(x)+g(x)也是R上的增函数,故D正确.1234567891011123456789101110.设f(x)是定义在(-1,1)上的偶函数,且f(x)在[0,1)上单调递减,f(- )=1,则f(x)<1的解集为　 　　　　. 123456789101111.[2023江苏扬州高一月考]已知函数f(x)=x|x|,则满足f(x)+f(3x-2)≥0的x的取值范围是　　　　　.(用区间表示) 解析 由题意f(x)=x|x|,其定义域为R,关于原点对称,f(-x)=-x|-x|=-x|x|=-f(x),所以函数f(x)是奇函数.