高考数学三轮冲刺卷：两角和与差的正切（含答案）

这是一份高考数学三轮冲刺卷：两角和与差的正切（含答案），共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（共20小题；）
1.
A. B. C. D.

2. 在 中，下列命题错误的是
A. 若 ，则 一定为钝角三角形
B. 若 ，则 一定为直角三角形
C. 若 ，则 一定为锐角三角形
D. 若 ，则 中角 为锐角

3. 设 ，，且 则
A. B. C. D.

4. 已知角 的终边经过点 ，则 的值是
A. B. C. D.

5. 若 ，则 等于
A. B. C. D. 不确定

6. ，， 是 的三个内角，且 ， 是方程 的两个实数根，则 是
A. 钝角三角形B. 锐角三角形C. 直角三角形D. 以上均有可能

7. 设 ， 是方程 的两个根，则 的值为
A. B. C. D.

8. 中，，，则
A. B. C. D.

9. 已知 ，则
A. B. C. D.

10. 已知 ，，则 在
A. 第一象限B. 第二象限C. 第三象限D. 第四象限

11. 若 ，，且 是第三象限的角，则 的值是
A. B. C. D.

12. 已知 ，， 是方程 的两根，则
A. B. 或 C. D.

13. 已知 ，，则 的值是
A. B. C. D.

14. 的值为
A. B. C. D.

15. 已知 ，，则
A. B. C. D.

16. 若 ， 是方程 的两根，且 ，则 等于
A. B. C. 或 D. 或

17. 已知 ，，那么 等于
A. B. C. D.

18. 设角 的终边过点 ，则
A. B. C. D.

19. 设 ，，，，， 都是非零实数，不等式 的解集为 ，不等式 的解集为 ，则“”是“”的
A. 充分非必要条件B. 必要非充分条件
C. 充分必要条件D. 既非充分又非必要条件

20. 如图，， 是半径为 的圆周上的定点， 为圆周上的动点， 是锐角，大小为 ．图中阴影区域的面积的最大值为
A. B. C. D.

二、填空题（共5小题；）
21. ．

22. 计算： ．

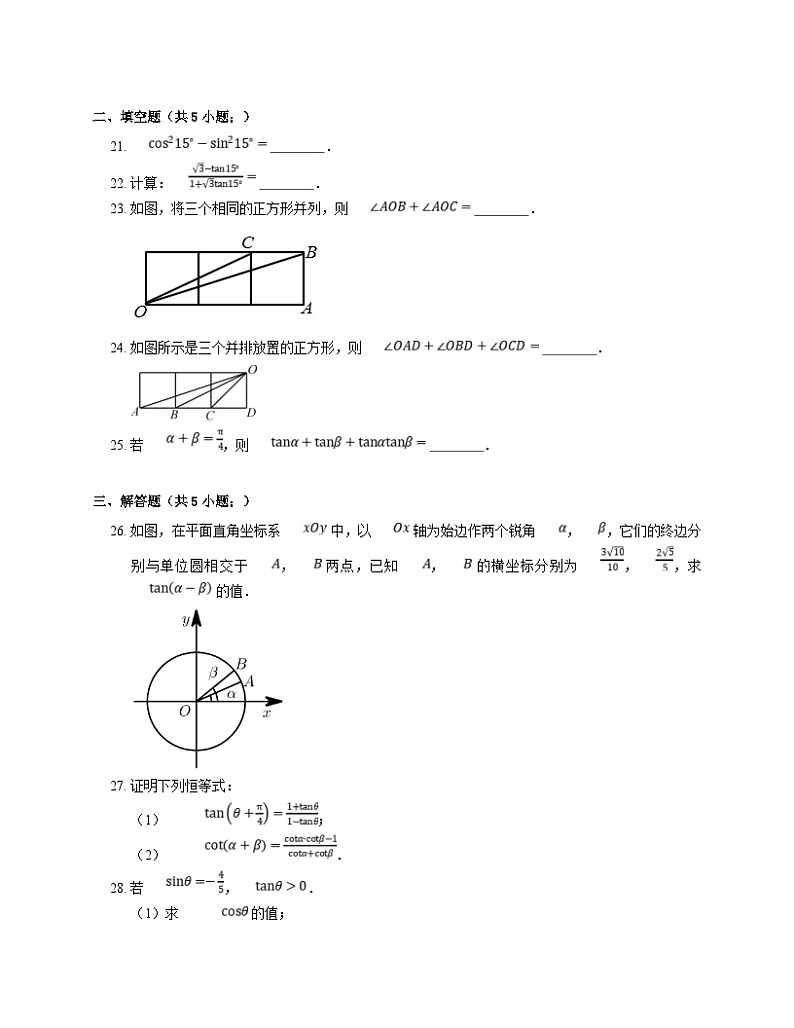
23. 如图，将三个相同的正方形并列，则 ．

24. 如图所示是三个并排放置的正方形，则 ．

25. 若 ，则 ．

三、解答题（共5小题；）
26. 如图，在平面直角坐标系 中，以 轴为始边作两个锐角 ，，它们的终边分别与单位圆相交于 ， 两点，已知 ， 的横坐标分别为 ，，求 的值．

27. 证明下列恒等式：
（1）；
（2）．

28. 若 ，．
（1）求 的值；
（2）求 的值．

29. 已知 ，求 的值．

30. 已知 ，，求值：
（1）．
（2）．
答案
1. D【解析】由两角和与差的正切公式知 ．
2. C【解析】， 为钝角，则 一定为钝角三角形；
， 为直角， 一定为直角三角形；
， 为锐角， 不一定为锐角三角形．
故C错误．
3. D
4. D
5. B
6. A
7. A【解析】因为 ， 是方程 的两个根，所以 ，，所以 ．
8. C
9. D【解析】由 ，得 ，
即 ，
得 ，
即 ，
即 ，
则 ，
故选：D．
10. D
【解析】由题意得，，
所以 ，即 ，
解得 ，
则 在第二或四象限，
由 得， 在第一或四象限，
所以 在第四象限．
11. D
12. D【解析】因为 ，
所以 ，
因为 ， 是方程 的两根，
所以 ，，，，
所以 ，
故 ，，
因为 ，
再根据 ，可得 ，
求得 （舍去）或 ．
13. B
14. A
15. B
16. B
17. A
18. A【解析】由于角 的终边过点 ，因此 ，故 ．
19. B
20. B
21.
22.
【解析】
23.
【解析】由图可知 ，．
所以 ．
因为 ，所以 ．
24.
25.
26. 由题可知：，，
由于 ， 为锐角，
则 ，，
故 ，，
则 ，
故答案为 ．
27. （1）
（2）
28. （1） 因为 ，，
所以 是第三象限角，．
由 ，得 ．
（2） 又 ，
所以 ．
29. 由 ，得 ，
于是原式 ．
30. （1） 因为 ，
所以 ，，，
所以 ，
因为 ，
所以 ，
，
所以 ．
（2）
因为
所以
所以